Динамика кривошипно-шатунного механизма

При работе двигателя в КШМ действуют следующие основные силовые факторы: силы давления газов, силы инерции движущихся масс механизма, силы трения и момент полезного сопротивления. При динамическом анализе КШМ силами трения обычно пренеб­регают.

8.2.1. Силы давления газов

Сила давления газов возникает в результате осуществления в ци­линдре двигателя рабочего цикла. Эта сила действует на поршень, и ее значение определяется как произведение перепада давления на поршне на его площадь: P_г = (p_г–p_о)F_п. Здесь р_г – давление в ци­линдре двигателя над поршнем; р_о– давление в картере; F_п– площадь дна поршня.

Для оценки динамической нагруженности элементов КШМ важ­ное значение имеет зависимость силы Р_гот времени. Ее обычно получают перестроением индикаторной диаграммы из координат р–V вкоординаты р—φ посредством определения V_φ =x_φ F_п с использованием зависимости (84) или графических методов.

Сила давления газов, действующая на поршень, нагружает под­вижные элементы КШМ, передается на коренные опоры картера и уравновешивается внутри двигателя за счет упругой деформации элементов, формирующих внутрицилиндровое пространство, силами Р_ги Р^/_г, действующими на головку цилиндра и на поршень. Эти силы не передаются на опоры двигателя и не вызывают его неуравновешенности.

8.2.2. Силы инерции движущихся масс КШМ

Реальный КШМ представляет собой систему с распределенными параметрами, элементы которой движутся неравномерно, что вы­зывает появление инерционных сил.

В инженерной практике для анализа динамики КШМ широко используют динамически эквивалентные ему систе­мы с сосредоточенными параметрами, синтезируемые на основе метода замещающих масс. Критерием эквивалентности является равенство в любой фазе рабочего цикла совокупных кинетических энергий эквивалентной модели и замещаемого ею механизма. Ме­тодика синтеза модели, эквивалентной КШМ, базируется на замене его элементов системой масс, связанных между собой невесомыми абсолютно жесткими связями.

• Детали поршневой группы совершают прямолинейное возвратно-поступательное движение вдоль оси цилиндра и при анализе ее инерционных свойств могут быть замещены равной им массой m_п, сосредоточенной в центре масс, положение которого практически совпадает с осью поршневого пальца. Кинематика этой точки описывается законами движения поршня, вследствие чего сила инерции поршня P_jп = –m_пj, где j –ускорение центра масс, равное ускоре­нию поршня.

 

 

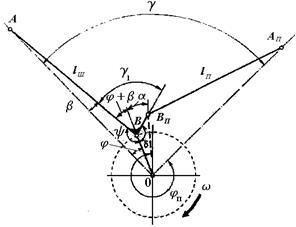
Рисунок 14 – Схема кривошипного механизма V-образного двигателя с прицепным шатуном

 

 

Рисунок 15 – Траектории точек подвеса главного и прицепного шатунов

• Кривошип коленчатого вала совершает равномерное вращательное движение. Конструктивно он состоит из совокупности двух половин коренных шеек, двух щек и шатунной шейки. Инерционные свойства кривошипа описываются суммой центробежных сил элементов, центры масс которых не лежат на оси его вращения (щеки и шатунная шейка): К_к=К_rш.ш+2К_rщ=т_ш.шrω ²+2т_щρ _щω ², где К_rш.ш К_rщи r, ρ _щ— центробежные силы и расстояния от оси вращения до центров масс соответственно шатунной шейки и щеки, m_ш.ш и m_щ— массы соответственно шатунной шейки и щеки.

• Элементы шатунной группы совершают сложное плоскопарал­лельное движение, которое может быть представлено как совокупность поступательного движения с кинематическими параметрами центра масс и вращательного движения вокруг оси, проходящей через центр масс перпендикулярно плоскости качания шатуна. В связи с этим ее инерционные свойства описываются двумя пара­метрами — инерционными силой и моментом.

Эквивалентная система, замещающая КШМ, представляет собой систему двух жестко связанных между собой масс:

• массу, сосредоточенную на оси пальца и совершающую возвратно-поступательное движение вдоль оси цилиндра с кинематическими параметрами поршня, m_j=m_п+m_ш.п;

• массу, расположенную на оси шатунной шейки и совершающую вращательное движение вокруг оси коленчатого вала, т_r=т_к+т_ш.к(для V-образных ДВС с двумя шатунами, распо­ложенными на одной шатунной шейке коленчатого вала, т_r= m_к+m_ш.к.

В соответствии с принятой моделью КШМ масса m_j вызывает силу инерции P_j= —m_jj, а масса т_r создает центробежную силу инерции К_r= — а_ш.шт_r=т_rrω ².

Сила инерции P_j уравновешивается реакциями опор, на которые установлен двигатель, Будучи переменной по величине и направле­нию, она, если не предусмотреть специальных мероприятий по ее уравновешиванию, может быть причиной внешней неуравновешен­ности двигателя, как это показано на рисунке 16, а.

При анализе динамики ДВС и особенно его уравновешенности с учетом полученной ранее зависимости ускорения j от угла поворо­та кривошипа φ силу инерции Р_j удобно представлять в виде суммы двух гармонических функций, которые отличаются амплитудой и скоростью изменения аргумента и называются силами инерции первого (P_jI) и второго (P_jII) порядка:

P_j= – m_jrω ²( cos φ +λ cos2φ ) = С cos φ + λ C cos 2φ =P_fI+P_jII,

где С = –m_jrω ².

Центробежная сила инерции K_r=m_rrω ² вращающихся масс КШМ представляет собой постоянный по величине вектор, направ­ленный от центра вращения по радиусу кривошипа. Сила К_r переда­ется на опоры двигателя, вызывая переменные по величине реакции (рисунок 16, б). Таким образом, сила К_r как и сила Р_j, может являться причиной неуравновешенности ДВС.

а – сила P_j; сила К_r; К_х=K_r cos φ = K_r cos (ω t); К_у = K_r sin φ = K_r sin (ω t)

Рис. 16 - Воздействие сил инерции на опоры двигателя:

 

⇐ Предыдущая123456789

Поделиться: