Вращение твердого тела (корабельного на волнении или сухопутного на грунте носителя) вокруг неподвижной точки (регулярная прецессия)
Схемы конструкций и исходные данные
Определить: угол нутации q, угловую скорость нутации  , прецессии
, прецессии  , ротации
, ротации  и мгновенную угловую скорость
и мгновенную угловую скорость  , угловое ускорение
, угловое ускорение  твердого тела; скорости и ускорения точек А, В, С подвижного конуса 1, катящегося без скольжения по неподвижному конусу 2 (рис. 4.1).
твердого тела; скорости и ускорения точек А, В, С подвижного конуса 1, катящегося без скольжения по неподвижному конусу 2 (рис. 4.1).
Задача сформулирована отдельно для каждого варианта, чертежи к задачам помещены на рис.4.1 (по последней цифре шифра (ПЦШ) выбирается номер схемы от 0 до 9), необходимые числовые данные, соответствующие (предпоследней цифре шифра (ПрЦШ) приведены в табл. 4.1. Во всех вариантах задачи
(рис. 4.1) рассматривается регулярная прецессия твердого тела.

Рис. 4.1. Схемы к расчетной работе №1
Т а б л и ц а 4.1
| Данные (ПрЦШ)=0
| Последняя цифра шифра (ПЦШ)
|
|
|
|
|
|
|
|
|
|
|
|
| h
| м
| 0, 12
| 0, 4
| 0, 2
| 0, 18
| 0, 1
| -
| 0, 2
| 0, 12
| 0, 12
| -
|
| R
| -
| 0, 8
| -
| -
| -
| 0, 3
| -
| -
| -
| 0, 18
|
| 2a
| град
|
| -
|
|
|
|
|
|
|
|
|
| 2b
| -
| -
| -
|
|
|
|
|
|
|
|
| vc
| м /с
| -
|
| -
| -
| 0, 2
| -
| -
| -
| -
| -
|
| a1
| м/с2
|
|
|
| 0, 36
| -
| -
| -
| 
| 0, 48
|
|
| n
| об/мин
|
| -
|
| -
| -
| 30/p
| -
| -
| -
|
|
| t
| с
| -
| -
| -
| -
| -
| -
|
| -
| -
| -
|
| Данные (ПрЦШ)=1
| Последняя цифра шифра (ПЦШ)
|
|
|
|
|
|
|
|
|
|
|
|
| h
| м
| 0, 12
| 
| 0, 4
| 0, 16
| 0, 15
| -
| 0, 3
| 0, 16
| 0, 16
| -
|
| R
| -
| 0, 5
| -
| -
| -
| 0, 25
| -
| -
| -
| 0, 24
|
| 2a
| град
|
| -
|
|
|
|
|
|
|
|
|
| 2b
| -
| -
| -
|
|
|
|
|
|
|
|
| vc
| м /с
| -
| 
| -
| -
| 0, 45
| -
| -
| -
| -
| -
|
| a1
| м/с2
|
| -
| -
| 0, 32
| -
| -
| -
| 
| 0, 72
|
|
| n
| об/мин
|
| -
|
| -
| -
| 60/p
| -
| -
| -
|
|
| t
| с
| -
| -
| -
| -
| -
| -
|
| -
| -
| -
|
| Данные (ПрЦШ)=2
| Последняя цифра шифра (ПЦШ)
|
|
|
|
|
|
|
|
|
|
|
|
| h
| м
| 0, 1
| 0, 5
| 0, 3
| 0, 15
| 0, 2
| -
| 0, 4
| 0, 2
| 0, 2
| -
|
| R
| -
| 1, 0
| -
| -
| -
| 0, 2
| -
| -
| -
| 0, 3
|
| 2a
| град
|
| -
|
|
|
|
|
|
|
|
|
| 2b
| -
| -
| -
|
|
|
|
|
|
|
|
| vc
| м /с
| -
|
| -
| -
| 0, 8
| -
| -
| -
| -
| -
|
| a1
| м/с2
|
| -
| -
| 0, 3
| -
| -
| -
| 
| 0, 8
|
|
| n
| об/мин
| 30/p
| -
|
| -
| -
| 90/p
| -
| -
| -
|
|
| t
| с
| -
| -
| -
| -
| -
| -
|
| -
| -
| -
|
Варианты 0, 2. Прямой круговой конус с углом 2aпри вершине катится без скольжения по неподвижной плоскости, делая n оборотов в минуту вокруг вертикальной оси OYв направлении, указанном стрелкой. Высота конуса OC = h.
Вариант 1. Прямой круговой конус катится без скольжения по неподвижной горизонтальной плоскости в направлении, указанном стрелкой. Высота конуса ОC = h, радиус основания равен R. Движение конуса происходит так, что скорость центра основания постоянна и равна vC.
Варианты 3…9. Конус 1 с углом 2aпри вершине катится без скольжения по неподвижному конусу 2 с углом 2b при вершине в направлении, указанном стрелкой. Высота конуса OC = h.
Движение конуса 1 происходит так:
· вар. 3 - осестремительное ускорение центра С основания конуса при его вращении вокруг вертикальной оси OY  постоянно и равно а1;
постоянно и равно а1;
· вар. 4 - скорость точки Сцентра основания конуса постоянна и равна vC , 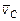 ↑ ↑ OZ в данный момент времени;
↑ ↑ OZ в данный момент времени;
· вар. 5 - подвижный конус 1 обегает неподвижный конус 2, совершая nоборотов в минуту, радиус основания конуса 1 равен R;
· вар. 6 - подвижный конус 1 совершает за время t один оборот вокруг вертикальной оси  против часовой стрелки;
против часовой стрелки;
· вар. 7 - вращательное ускорение центра С основания конуса 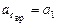 ;
;
· вар. 8 - ускорение точки Мконуса 1, лежащей на середине его образующей, равно  , причем
, причем  ;
;
· вар. 9подвижный конус 1 совершает n оборотов в минуту вокруг своей оси симметрии Оy.
Указания и план выполнения
Случай регулярной прецессии – это такое вращение твердого тела вокруг неподвижной точки, при котором (рис. 4.2) во все время движения остаются постоянными:
· угол нутации  ,
, 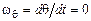 ;
;
· угловые скорости прецессии, ротации и мгновенная угловая скорость (  );
);
 ;
;
· угловое ускорение  .
.
 1. Найти неподвижную точку вращающегося тела, выбираемую за начало отсчета
1. Найти неподвижную точку вращающегося тела, выбираемую за начало отсчета
неподвижной и связанной
координатных систем. Выбрать оси прецессии  ,
,
ротации  , нутации
, нутации  (
( 
 или
или  ¯
¯  ).
).
2. Определить угловые скорости нутации  , прецессии
, прецессии  , ротации
, ротации  и мгновенную угловую скорость
и мгновенную угловую скорость  и мгновенную ось вращения
и мгновенную ось вращения  .
.
В зависимости от задания движения твердого тела вектор  можно определять двумя способами:
можно определять двумя способами:
1) по ее составляющим  ;
;
2) использовать мгновенную ось вращения  , которую в дальнейшем будем для краткости обозначать
, которую в дальнейшем будем для краткости обозначать 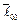 . По известной скорости
. По известной скорости  какой-либо точки Мтвердого тела и положению оси
какой-либо точки Мтвердого тела и положению оси 
 находят величину
находят величину  :
: 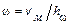 , где
, где 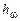 – перпендикуляр, опущенный из точки Мна ось
– перпендикуляр, опущенный из точки Мна ось 
 .
.
3. Определить угловое ускорение  твердого тела. В случае регулярной прецессии
твердого тела. В случае регулярной прецессии  и является закрепленным в точке О вектором, положительное направление которого определяется как результат векторного произведения.
и является закрепленным в точке О вектором, положительное направление которого определяется как результат векторного произведения.
4. Определить скорости произвольных точек твердого тела по формуле Эйлера  , величина которой
, величина которой 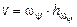 .
.
5. Определить ускорения  произвольных точек твердого тела по формуле
произвольных точек твердого тела по формуле 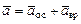 , где
, где  - вектор осестремительного ускорения, величина которого
- вектор осестремительного ускорения, величина которого  ;
;  - вектор вращательного ускорения, величина которого
- вектор вращательного ускорения, величина которого  .
.
Так как  всегда направлено от точки по
всегда направлено от точки по 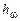 к оси
к оси 
 , можно не пользоваться векторной формой для
, можно не пользоваться векторной формой для  . Что же касается
. Что же касается  , то его следует находить только по векторной форме.
, то его следует находить только по векторной форме.
Поскольку при вращении около полюса вектор  неколлинеарен
неколлинеарен  , то
, то  и
и  , вообще говоря, не являются перпендикулярными векторами, поэтому определение
, вообще говоря, не являются перпендикулярными векторами, поэтому определение 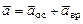 должно производиться после построения векторов на чертеже, и величина ускорения будет равна
должно производиться после построения векторов на чертеже, и величина ускорения будет равна
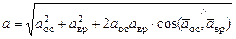 .
.
Для точек, лежащих на оси ротации твердого тела, справедливы также следующие зависимости:
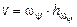 и
и 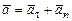 ,
,
где  – нормальное ускорение;
– нормальное ускорение;  – касательное ускорение, при регулярной прецессии
– касательное ускорение, при регулярной прецессии 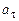 =0.
=0.
Все векторы, лежащие в плоскости OXY(плоскости чертежа), должны быть изображены в этой плоскости; направление же других векторов должно быть указано в тексте.
Пример 1. Дано. Конус 1 с углом 2a = 60° при вершине
(рис. 4.3) катится по неподвижному конусу 2 с углом 2b=120° при вершине без скольжения, приэтом вершина О конуса 1 остается неподвижной, а центр С его основания движется по окружности, расположенной в горизонтальной плоскости, с постоянной
скоростью  , причем
, причем  ,
,  =3 м/с, ОА=ОВ=2м.
=3 м/с, ОА=ОВ=2м.
Определить.1. Угол нутации q, угловую скорость нутации  , прецессии
, прецессии  , ротации
, ротации  и мгновенную угловую скорость
и мгновенную угловую скорость  . 2. Угловое ускорение конуса
. 2. Угловое ускорение конуса  . 3. Скорости точек А и В
. 3. Скорости точек А и В  ,
,  . 4. Ускорения точек А, В, С
. 4. Ускорения точек А, В, С  (найти осестремительное
(найти осестремительное  и вращательное
и вращательное  ускорения точки С).
ускорения точки С).

Рис. 4.3
Решение.Введем неподвижную систему координат OXYZ с началом в точке О конуса 1. Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось  вращения конуса 1 совпадает с образующей ОА.
вращения конуса 1 совпадает с образующей ОА.
1. Угол нутации  , поскольку с конца оси нутации ОЕ поворот от оси прецессии OY к оси ротации Oy кажется против часовой стрелки;
, поскольку с конца оси нутации ОЕ поворот от оси прецессии OY к оси ротации Oy кажется против часовой стрелки;  .
.
2. Траекторией точки С, с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения  и центр которой лежит на
и центр которой лежит на  , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси.
, с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси.
Установив положение мгновенной оси вращения, найдем модуль мгновенной угловой скорости конуса. Поскольку
 , (4.1)
, (4.1)
где  – кратчайшее расстояние от точки С до мгновенной оси
– кратчайшее расстояние от точки С до мгновенной оси  ;
;  , то
, то
 . (4.2)
. (4.2)
Учитывая заданное направление вектора 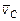 ,
,  , отложим от точки О вдоль мгновенной оси
, отложим от точки О вдоль мгновенной оси  = ОА вектор
= ОА вектор  так, чтобы видеть с его конца вращение конуса вокруг этой оси
так, чтобы видеть с его конца вращение конуса вокруг этой оси  в направлении, противоположном направлению движения часовой стрелки (рис. 4.3).
в направлении, противоположном направлению движения часовой стрелки (рис. 4.3).
С другой стороны, поскольку центр С основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то
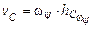 , (4.3)
, (4.3)
где  – кратчайшее расстояние от точки С до оси ОY, равное
– кратчайшее расстояние от точки С до оси ОY, равное 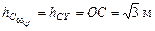 .
.
Отсюда находим величину угловой скорости прецессии  :
:
 . (4.4)
. (4.4)
Направление вектора  определим в зависимости от задания движения конуса 1, в данном случае вращение конуса 1 вокруг оси прецессии происходит по часовой стрелке, поэтому
определим в зависимости от задания движения конуса 1, в данном случае вращение конуса 1 вокруг оси прецессии происходит по часовой стрелке, поэтому  ¯
¯ 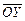 (оси прецессии).
(оси прецессии).
3. Векторное равенство  , в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величину угловой скорости ротации, а именно:
, в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величину угловой скорости ротации, а именно:  ; линией действия вектора
; линией действия вектора  является мгновенная ось вращения
является мгновенная ось вращения  ; линией действия вектора
; линией действия вектора  ¯
¯ 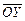 - ось прецессии OY, линией действия вектора
- ось прецессии OY, линией действия вектора  - ось ротации Оy (рис. 4.3). Таким образом, величина угловой скорости ротации
- ось ротации Оy (рис. 4.3). Таким образом, величина угловой скорости ротации
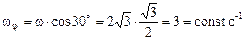 . (4.5)
. (4.5)
4. Угловое ускорение  в случае регулярной прецессии определяется векторным произведением
в случае регулярной прецессии определяется векторным произведением  , т.е. вектор
, т.е. вектор  ¯
¯  , так какс конца оси OZ поворот от вектора
, так какс конца оси OZ поворот от вектора  к вектору
к вектору  кажется по ходу часовой стрелки; величина углового ускорения
кажется по ходу часовой стрелки; величина углового ускорения
 рад/с2 . (4.6)
рад/с2 . (4.6)
5. Скорости точек конуса 1:
· точки А  , так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;
, так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;
· точки В  , где
, где  ,
,  и вектор
и вектор  ¯
¯  .
.
6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.
Для точки А:  ;
;  ;
;  ;
;
 ;
;  ,
,
где  ;
;  м.
м.
Вектор  направлен перпендикулярно плоскости, в которой лежат векторы
направлен перпендикулярно плоскости, в которой лежат векторы  и
и 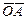 , т.е. перпендикулярно ОА в сторону
, т.е. перпендикулярно ОА в сторону  .
.
Таким образом, 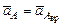 ;
;  .
.
Для точки В:  ;
;  ;
;  .
.
Вектор  направлен от точки B к мгновенной оси вращения конуса 1 (рис. 4 3). Вектор
направлен от точки B к мгновенной оси вращения конуса 1 (рис. 4 3). Вектор  перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы  и
и  , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону  . Величины этих векторов:
. Величины этих векторов: 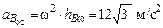 ;
;  , где
, где  м.
м.
Полное ускорение точки B найдем как диагональ прямоугольника, построенного на векторах  :
:

Для точки С:
а) 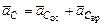 ;
;  ;
; 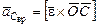 ;
;
 ;
; 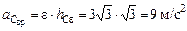 .
.
Вектор 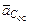 направлен от точки С к мгновенной оси вращения кoнуса 1.
направлен от точки С к мгновенной оси вращения кoнуса 1.
Вектор  перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы  и
и 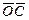 , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону  (рис. 4.3);
(рис. 4.3);
б) 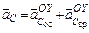 ;
; 
Ответ. 1. Угол нутации q = p/2; угловая скорость нутации  ; прецессии
; прецессии  1/с; ротации
1/с; ротации  1/с; мгновенная угловая скорость
1/с; мгновенная угловая скорость  1/с. 2. Угловое ускорение конуса
1/с. 2. Угловое ускорение конуса  1/с2. 3. Скорости точек А и В
1/с2. 3. Скорости точек А и В  м/с.
м/с.
4. Ускорения точек А, В, С 
 м/c2; осестремительное ускорение точки С
м/c2; осестремительное ускорение точки С 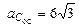 м/с2; вращательное ускорение точки С
м/с2; вращательное ускорение точки С  м/с2.
м/с2.
Пример 2. Дано. Конус 1 с углом 2a при вершине катится без скольжения по неподвижному конусу 2 с углом 2b при вершине в направлении, указанном стрелкой (рис. 4.4). Высота конуса OC = h. Вращательное ускорение центра С основания конуса  =0, 48 м/с2, h=0, 12 м, 2α = 120°, 2β = 60°.
=0, 48 м/с2, h=0, 12 м, 2α = 120°, 2β = 60°.
Определить. 1. Угол нутации q, угловую скорость нутации  , прецессии
, прецессии  , ротации
, ротации  и мгновенную угловую скорость
и мгновенную угловую скорость 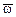 . 2. Угловое ускорение конуса
. 2. Угловое ускорение конуса  . 3. Скорости точек А, В, С
. 3. Скорости точек А, В, С  . 4. Ускорения точек А, В, С
. 4. Ускорения точек А, В, С  .
.
Решение. Введем неподвижную систему координат OXYZ с началом в точке О конуса 1. Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось вращения  кону
кону  са 1 совпадает с образующей ОА.
са 1 совпадает с образующей ОА.
1. Угол нутации:  , так как с конца оси нутации ОZ=OE поворот от оси прецессии OY к оси ро-тации Оy кажется про-
, так как с конца оси нутации ОZ=OE поворот от оси прецессии OY к оси ро-тации Оy кажется про-
тив часовой стрелки,  .
.
2. Направление вектора  определяется в зависимости от задания движения конуса 1 вокруг оси прецессии OY, в данном случае – против часовой стрелки, поэтому
определяется в зависимости от задания движения конуса 1 вокруг оси прецессии OY, в данном случае – против часовой стрелки, поэтому  ↑ ↑
↑ ↑ 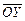 .
.
3. Векторное равенство  , в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величины угловых скоростей прецессии и ротации через мгновенную угловую скорость вращения
, в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и величины угловых скоростей прецессии и ротации через мгновенную угловую скорость вращения 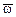 . Так как линия действия вектора
. Так как линия действия вектора  – ось прецессии OY, причем
– ось прецессии OY, причем  ↑ ↑
↑ ↑ 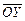 , линией действия вектора
, линией действия вектора 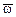 является мгновенная ось вращения
является мгновенная ось вращения  ; линией действиявектора
; линией действиявектора  – ось ротации Оy, то из векторного равенства
– ось ротации Оy, то из векторного равенства 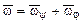 следует, что
следует, что 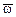 ↑ ↑
↑ ↑ 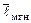 , а
, а  ↑ ↑
↑ ↑  , а величины угловых скоростей прецессии и ротации равны
, а величины угловых скоростей прецессии и ротации равны  1/с = const,
1/с = const,  1/с = const.
1/с = const.
4.Угловое ускорение  в случае регулярной прецессии определяется векторным произведением
в случае регулярной прецессии определяется векторным произведением  , т.е. вектор
, т.е. вектор 
 , так какс конца оси OZ поворот вектора
, так какс конца оси OZ поворот вектора  к вектору
к вектору 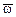 кажется против хода часовой стрелки; величина углового ускорения
кажется против хода часовой стрелки; величина углового ускорения  1/с2 .
1/с2 .
С другой стороны, по заданному  , где
, где  , находим величину углового ускорения
, находим величину углового ускорения  . Направление вектора
. Направление вектора  указано в условии. Вектор
указано в условии. Вектор  лежит в плоскости (ВОА), перпендикулярен плоскости, в которой лежат векторы
лежит в плоскости (ВОА), перпендикулярен плоскости, в которой лежат векторы  и
и  , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону  .
.
Таким образом, используя полученные равенства  ,
,  ,
,  , находим величины
, находим величины  1/с,
1/с,  1/с,
1/с,  1/с.
1/с.
5. Скорости точек конуса 1:
· точки А:  , так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;
, так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;
· точки В:  , где
, где  (см. рис. 4.4),
(см. рис. 4.4),  и вектор
и вектор 
 ;
;
· точки С. Траекторией точки С, с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения  и центр которой лежит на
и центр которой лежит на  , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси. Поэтому скорость точки С конуса 1 можно определить по двум формулам:
, с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси. Поэтому скорость точки С конуса 1 можно определить по двум формулам:
1)  , где
, где  – кратчайшее расстояние от точки С до мгновенной оси вращения
– кратчайшее расстояние от точки С до мгновенной оси вращения  ,
, 
 ;
;  ,
, 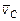
 .
.
С другой стороны, поскольку центр С основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то
2)  , где
, где  – кратчайшее расстояние от точки С до оси ОY ,
– кратчайшее расстояние от точки С до оси ОY , 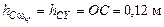 ;
;  =
=  .
.
6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.
Для точки А:
а)  ;
;  ;
;  ;
;
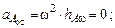 так как
так как  ;
;
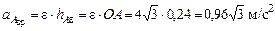 ;
;
 .
.
Вектор  направлен перпендикулярно плоскости, в которой лежат векторы
направлен перпендикулярно плоскости, в которой лежат векторы  и
и 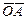 , т.е. перпендикулярно ОА в сторону
, т.е. перпендикулярно ОА в сторону  . Таким образом,
. Таким образом,  м/с2.
м/с2.
Для точки В:  ;
;  ;
;  .
.
Вектор 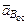 направлен от точки B по
направлен от точки B по  к мгновенной оси вращения
к мгновенной оси вращения  конуса 1. Вектор
конуса 1. Вектор  перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы  и
и  , принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону  .
.

 .
.
Полное ускорение точки B найдем через его проекции на оси дополнительной системы координат  , лежащей в плоскости (BOA), как
, лежащей в плоскости (BOA), как
 :
:
 м/с2;
м/с2;
 м/с2.
м/с2.
Для точки С:
1) 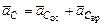 ;
;  ;
;  ;
;
 м/с2;
м/с2;
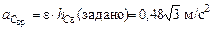 .
.
Вектор  направлен от точки С по
направлен от точки С по  к мгновенной оси вращения конуса. Направление вектора
к мгновенной оси вращения конуса. Направление вектора  указано в условии. Вектор
указано в условии. Вектор  направлен перпендикулярно ОС в сторону
направлен перпендикулярно ОС в сторону  ;
;
2) 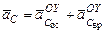 ;
; 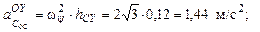

Причем, величину вектора  можно получить как
можно получить как  = =0, 48∙ 3=1, 44 м/с2.
= =0, 48∙ 3=1, 44 м/с2.
Ответ. 1. Угол нутации q = p/2; угловая скорость нутации  ; угловые скорости прецессии
; угловые скорости прецессии  1/с; ротации
1/с; ротации  рад/с; мгновенная угловая скорость
рад/с; мгновенная угловая скорость  = 4 рад/с.
= 4 рад/с.
2. Угловое ускорение конуса  рад/с2.
рад/с2.
3. Скорости точек А, В, С:  =0;
=0;  ;
;  м/с.
м/с.
4. Ускорения точек А, В, С: 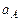 = 0, 96
= 0, 96  м/с2;
м/с2;  = 4, 4 м/с2;
= 4, 4 м/с2;
 = 1, 44 м/с2.
= 1, 44 м/с2.
5. Осестремительное ускорение точки С  = 0, 96
= 0, 96  м/с2.
м/с2.
6. Вращательное ускорение точки С (задано)
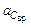 = 0, 48
= 0, 48  м/с2 .
м/с2 .
Расчетная работа № 2

