Причины возникновения переходных процессов в электрических цепях. Законы коммутации.
Любое изменение в электрической цепи, связанное с изменением параметров или схемы цепи, называется коммутацией. Коммутация приводит к возникновению переходного процесса.
Возникновение переходного процесса объясняется тем, что если в цепи имеются индуктивность и (или) емкость переход от одного установившегося режима (до коммутации) к другому (после коммутации) не может совершиться мгновенно даже при мгновенной коммутации, поскольку не может мгновенно измениться энергия магнитного и электрических полей, связанных с индуктивностью и емкостью. Для мгновенного или скачкообразного изменения энергии полей необходима бесконечно большая мощность источника энергии, а таких источников не существует.
Из невозможности изменения скачком энергии полей, связанных с индуктивностью и емкостью, следуют законы коммутации.
Первый закон коммутации: в начальный момент после коммутации ток в индуктивности остается таким же, каким он был непосредственно перед коммутацией, iL(0+) = iL(0-). (3.1)Второй закон коммутации: в начальный момент после коммутации напряжение на емкости остается таким же, каким оно было непосредственно перед коммутацией,
uс(0+) = uс(0-).
48.Общие сведения об анализе переходных процессов. Установившиеся и свободные составляющие электрических токов и напряжений. Анализ переходных процессов основан на составлении и решении уравнений Кирхгофа для мгновенных значений токов и напряжений. В результате решения уравнений находится ток (напряжение) переходного процесса i(t), который называется переходным током (напряжением). После окончания переходного процесса в цепи наступает установившийся режим, который определяется источниками э.д.с. и параметрами R, L и С цепи.
Уравнения Кирхгофа для мгновенных значений токов (напряжений) являются дифференциальными. В конечном итоге анализ переходных процессов заключается в решении дифференциальных уравнений. Для электрических цепей с линейными элементами, имеющими постоянные параметры R, L и С, эти уравнения приводятся к линейным неоднородным дифференциальным уравнениям Как известно, общее решение линейного неоднородного дифференциального уравнения равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения  или
или  , (где iy(t), uу(t) – любое частное решение неоднородного уравнения (уравнения с правой частью); iсв(t), uсв(t)– общее решение однородного уравнения (уравнения без правой части).Частное решение iy(t)или uу(t) выражает установившийся режим, задаваемый источниками э.д.с. (тока). Установившийся ток iy(t) и напряжение uу(t) находятся методами, известными из анализа цепей постоянного и синусоидального тока.
, (где iy(t), uу(t) – любое частное решение неоднородного уравнения (уравнения с правой частью); iсв(t), uсв(t)– общее решение однородного уравнения (уравнения без правой части).Частное решение iy(t)или uу(t) выражает установившийся режим, задаваемый источниками э.д.с. (тока). Установившийся ток iy(t) и напряжение uу(t) находятся методами, известными из анализа цепей постоянного и синусоидального тока.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими тока iсв(t) или напряжения uсв(t). Решение однородного (без правой части ) линейного дифференциального уравнения может быть представлено в виде
49.Переходные процессы при включении R, Lна постоянное напряжение.. Пусть в момент времени t=0 цепь, состоящая из сопротивления R и индуктивности L, соединенных последовательно, включается на постоянное напряжение U (рис. 3.1.). По второму закону Кирхгофа
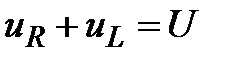
.
Так как  и
и  ,
,
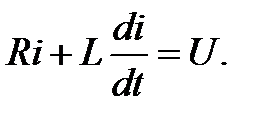
Характеристическое уравнение
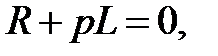
корень характеристического уравнения
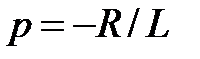
. Отсюда, на основании (3.4), свободный ток
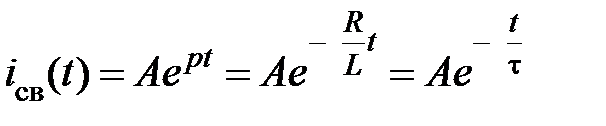
, где
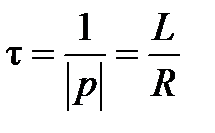
– постоянная времени.Тогда переходный ток, согласно (3.5),
 . (3.6)
. (3.6)
Индуктивность не оказывает влияния на постоянный ток, поэтому установившийся ток  . Следовательно,
. Следовательно,  .Постоянная интегрирования А находится из начальных условий (первый закон коммутации). При t=0 i=0 из (3.6) следует
.Постоянная интегрирования А находится из начальных условий (первый закон коммутации). При t=0 i=0 из (3.6) следует
 откуда
откуда 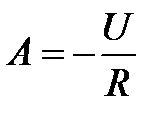 .
.
Следовательно,  (3.7)
(3.7)
где I=U/R –предельное значение, к которому стремится переходный ток.
Теоретически длительность переходного процесса бесконечна. В момент времени
t=τ, на основании (3.7),
i(
t)
=0, 63
I, а в момент времени
t=4τ
i(
t)
=0, 982
I. Поэтому длительностью этого переходного процесса принято называть время, равное 4
τ , по истечении которого величина переходного тока отличается от своего установленного значения менее чем на 2%.
На рис. 3.2 показана зависимость переходного тока в R, L цепи от времени.


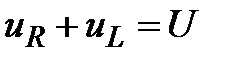 .
.
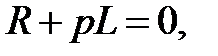 корень характеристического уравнения
корень характеристического уравнения 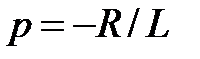 . Отсюда, на основании (3.4), свободный ток
. Отсюда, на основании (3.4), свободный ток 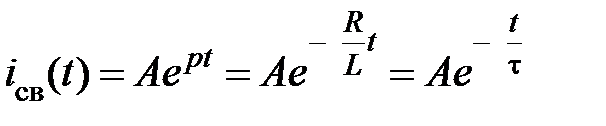 , где
, где 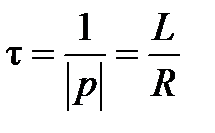 – постоянная времени.Тогда переходный ток, согласно (3.5),
– постоянная времени.Тогда переходный ток, согласно (3.5),