Работа 51. Экспериментальная проверка закона полного тока

Цель работы

Экспериментально подтвердить справедливость закона полного тока.

1. Приборы и принадлежности:

1. Большая катушка

2. Амперметр

3. Баллистический гальванометр

4. Переключатель

5. Источник электрического тока

6. Малая катушка

Краткая теория

Как показывает опыт, в пространстве, окружающем неподвижные электрические заряды, возникает электростатическое поле, а в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным.

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Отличительная особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрическиезаряды.

Так как магнитное поле является силовым, то его по аналогии с электрическим графически изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции . Их направление определяется правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

Физическое толкование магнитной индукции можно дать из закона Ампера:

.

Если угол между и равен , то . Тогда , откуда

.

Магнитная индукция В численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, по которому течет ток единичной силы и который расположен перпендикулярно к направлению поля.

характеризует силовое действие магнитного поля на движущийся электрические заряды (токи0 и является аналогом напряженности электрического поля , которая характеризует силовое действие электрического поля на заряд в данной точке поля.

Наряду с для описания магнитного поля в вакууме вводится величина , называемая напряженностью магнитного поля (аналог ).

В случае однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

,

где m₀ – магнитная постоянная , m – безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды, .

Таким образом, если известна величина индукции магнитного поля , то легко может быть рассчитана величина напряженности магнитного поля и наоборот. Индукция магнитного поля в ряде случаев может быть рассчитана на основании закона Био-Савара-Лапласа. Однако иногда прямое использование этого закона не позволяет решить задачу. В таких случаях индукция магнитного поля может быть определена с использованием закона полного тока.

Закон полного тока формулируется следующим образом:

Циркуляция вектора напряженности вдоль произвольного замкнутого контура равна алгебраической сумме токов, охватываемых этим контуром.

Математически запись закона полного тока имеет вид:

, (1)

где I_i – значение токов проводимости.

Рассмотрим магнитное поле бесконечно длинного прямолинейного проводника с током I. Линии напряженности магнитного поля этого тока – концентрические окружности, лежащие в плоскости, перпендикулярной

Рис. 1

r

B

проводнику с током (касательные к этим линиям параллельны ).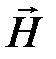

Циркуляция вектора напряженности этого поля вдоль произвольной силовой линии l (окружности радикса r) равна

.

Во всех точках окружности l

, ,

Следовательно .

Тогда

.

Таким образом

. (2)

Полученный результат верен для проводника с током любой геометрической формы при обходе по замкнутому контуру, охватывающему его.

Если магнитное поле создано системой токов I₁, I₂, …, I_n, то вектор напряженности будет равен геометрической сумме напряженностей полей, создаваемых каждым током в отдельности.

Поэтому формулу (2) можно записать в общем виде:

. (3)

Если контур не охватывает провод с током, то

.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром.

Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта, ток противоположного направления считается отрицательным.

Для экспериментальной проверки закона полного тока (1) поступим следующим образом. Выберем два произвольных контура. Пусть первый охватывает проводники с током, а второй не охватывает их. Разобьем контур на участки конечной длины Dl_i, определим на каждом участке экспериментальное значение H_i и сосчитаем сумму

.

При обходе контура эта сумма должна равняться сумме токов , величина которых в опыте изменяется. Обход второго контура должен показать, что

.

Форма контуров может быть выбрана любой. Однако в том случае, когда контур прямоугольный, равенство

является наиболее точным. Поэтому в опыте рекомендуется использовать прямоугольный контур обхода.

Для экспериментального определения величины воспользуемся явлением электромагнитной индукции. Маленькую катушку размеры которой м, подсоединим к баллистическому гальванометру. Пусть в какой-нибудь точке пространства напряженность поля изменяется от нуля до некоторого значения . Это происходит в момент, когда подается питание на проводники электрического тока.

Изменение напряженности за время включения Dt равно DН = Н. Катушка, замкнутая на гальванометр, располагается так, чтобы плоскость ее витков была перпендикулярна вектору . В этом случае

, (4)

где - составляющая вектора напряженности, совпадающая по направлению с вектором . В момент включения (или выключения) тока катушку пронизывает переменный магнитный поток. Его величина изменяется от нуля до , так что изменение магнитного потока равно .

Значение магнитного потока определяется так:

,

где S – площадь витка катушки. Таким образом, величина магнитного потока зависит от величины составляющей вектора напряженности, совпадающей по направлению с элементом контура Dl.

Согласно закону электромагнитной индукции ЭДС индукции определяется так:

. (5)

В соответствии с законом Ома для замкнутой цепи сила тока, проходящего через гальванометр, равна

, (6)

где R – сопротивление малой катушки; r – внутреннее сопротивление гальванометра.

Отсюда

, (7)

где - величина заряда, прошедшего через гальванометр за время .

Подставим ЭДС из (7) в формулу (5). Тогда

,

или, так как , то

. (8)

Величина отклонения светового пятна гальванометра пропорциональна заряду:

a ~ q. (9)

Используя соотношения (8) и (9), можно записать

,

где К – коэффициент пропорциональности.

Описание установки

Основным элементом установки (рис. 2) является катушка (1), изготовленная из немагнитного материала.

Г

А

. 0

II

I

Рис. 2

На ней намотано N витков провода, средний радиус катушки равен R. Катушка устанавливается на подставке (6). На этой же подставке закреплен стол (2), перпендикулярный плоскости катушки и проходящий через ее центр (0). На столе размечают два контура обхода: контур I охватывает все N витков катушки, а контур II не охватывает витки катушки.

Контуры разделены на отрезки равной длины Dl = 3 см.

Катушка с помощью двухполюсного переключателя подключается к постоянному источнику напряжения. В ее цепь включен амперметр (5).

Маленькая катушка (4) изготовлена из немагнитного материала и для удобства использования имеет квадратную форму. Катушка замкнута на баллистический гальванометр (3).

Выполнение работы

Работа выполняется в два этапа. На первом этапе определяется коэффициент пропорциональности между напряженностью магнитного поля и углом отклонения светового пятна гальванометра, а на втором определяется циркуляция вектора напряженности вдоль двух контуров.

I этап. Определение коэффициента пропорциональности между значением напряженности и углом отклонения светового пятна гальванометра.

Выберем такую точку магнитного поля, в которой напряженность поля легко подсчитать по измеренной величине тока. Такой точкой является центр катушки. Напряженность поля в центре кругового тока определяется формулой

.

Число витков в нашей катушке равно N. Так как длина катушки мала по сравнению с ее радиусом R, то напряженность поля в центре катушки равна

. (10)

Установим малую катушку в центр большой так, чтобы плоскости обеих катушек совпали. В этом случае напряженность поля перпендикулярна плоскости малой катушки. Выполним опыты по измерению угла отклонения светового пятна гальванометра при включении (или выключении) питания большой катушки. Одновременно следует измерять силу тока в большой катушке. Так как , то с учетом формулы (10) можно записать

,

или

. (11)

Результат следует записать в таблицу.

Таблица 1

№	a	I	R	N	К
	м	А	М		А/м2

Выполнив расчет по формуле (11), можно определить коэффициент К.

II этап. Расчет циркуляции вектора напряженности.

Опыт выполняется следующим образом. В пределах отрезка большого контура (контур I) устанавливается маленькая катушка перпендикулярно линии отрезка. Подается питание на большую катушку и определяется величина и направление отклонения a. Результаты записываются в таблицу 2. Если при включении питания световое пятно отклонилось вправо (или влево), то это направление следует принять за положительное. На следующем отрезке катушка устанавливается точно таким же образом. Она должна перемещаться так, чтобы новое ее положение было параллельно предыдущему. Если этого не соблюдать, то направление отклонения изменится и его можно ошибочно учесть как отрицательное. При переходе на очередной отрезок, перпендикулярный предыдущему, маленькая катушка поворачивается на угол 90° и тем самым устанавливается перпендикулярно линиям обхода. В процессе опыта следует контролировать наличие тока в большой катушке.

Опыты повторяют для контура II. Результаты опытов заносятся в таблицу 3.

Таблица 2.

Опыты с контуром I

№

a

№

a

Таблица 2

Опыты с контуром II

№
a

На основании опытных данных нужно подсчитать следующую сумму для каждого контура:

.

Затем подсчитать сумму токов внутри контура

.

Величины и должны быть равны (с учетом погрешностей измерений), что и подтверждает справедливость закона полного тока

5. Контрольные вопросы

1. Что такое индукция и напряженность магнитного поля?

2. Что такое полный ток?

3. Сформулировать закон полного тока.

4. Почему в опыте необходимо малую катушку устанавливать перпендикулярно линиям обхода контура?

5. Как изменится направление вектора напряженности, если изменить направление тока в большой катушке?

6. Если малую катушку повернуть относительно вертикальной оси на 180°, то направление отклонения гальванометра изменится. Объясните, почему это происходит.

7. Почему при включении и выключении тока в большой катушке отклонения светового пятна гальванометра происходят в разные стороны?

8. В чем заключается явление взаимоиндукции? Как оно используется в данной работе?

9. Почему отклонение светового пятна гальванометра пропорционально напряженности магнитного поля?

10. Чему равна напряженность магнитного поля в центре катушки с током?

11. Записать и сформулировать закон Фарадея-Ленца.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: