Методы решения неравенств, содержащих знак модуль.
Методы решения неравенств, содержащих знак модуль.
I) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если 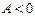 , то решений нет
, то решений нет
Если  , то
, то 
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
II) Неравенства вида 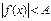 решаются следующим образом.
решаются следующим образом.
Если 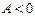 , то решений нет
, то решений нет
Если  , то решений нет
, то решений нет
Если  , то неравенству
, то неравенству 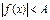 равносильна система
равносильна система 
III) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если 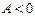 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 
Если  , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 
Если  , то неравенству
, то неравенству  равносильна совокупность
равносильна совокупность 
IV) Неравенства вида 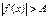 решаются следующим образом.
решаются следующим образом.
Если 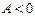 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 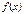
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 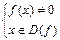
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 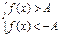
V) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству 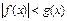 равносильна система
равносильна система 
VI) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству  соответствует уравнение
соответствует уравнение 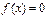
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
VII) Неравенства вида 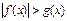 решаются следующим образом.
решаются следующим образом.
Если  , то неравенство
, то неравенство 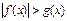 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
Если  , то неравенству
, то неравенству 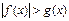 равносильна совокупность
равносильна совокупность 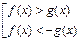
VIII) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то неравенство
, то неравенство  верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенство
, то неравенство 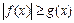 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенству
, то неравенству 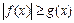 равносильна совокупность
равносильна совокупность 
IX) Неравенства вида  и
и  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует неравенство
соответствует неравенство 
Неравенству  соответствует неравенство
соответствует неравенство 
X) Решение неравенств используя определение модуля (общий способ).
P.S
Любое неравенство можно решит общим способом.
Методы решения уравнений, содержащих знак модуль.
I) Уравнения вида  решаются следующим образом.
решаются следующим образом.
Если  , то корней нет.
, то корней нет.
Если 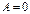 , то уравнению
, то уравнению  соответствует уравнение
соответствует уравнение 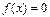
Если 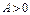 , то уравнению
, то уравнению  соответствует равносильная совокупность
соответствует равносильная совокупность 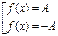
II) Уравнения вида  решаются следующим образом.
решаются следующим образом.
Способ №1
Уравнению  соответствует равносильная совокупность систем
соответствует равносильная совокупность систем 
Способ №2
Уравнению  соответствует равносильная совокупность систем
соответствует равносильная совокупность систем 
III) Уравнения вида  решаются следующим образом.
решаются следующим образом.
Способ №1
Уравнению  соответствует равносильное уравнение
соответствует равносильное уравнение 
Способ №2
Уравнению  соответствует равносильная совокупность
соответствует равносильная совокупность 
IV) Уравнения вида  и
и  решаются следующим образом.
решаются следующим образом.
Уравнению  соответствует равносильное неравенство
соответствует равносильное неравенство 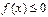
Уравнению 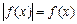 соответствует равносильное неравенство
соответствует равносильное неравенство 
Методы решения иррациональных неравенств.
I) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству 
соответствует равносильная система 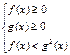
II) Неравенствах вида 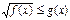 решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству 
соответствует равносильная система 
III) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная совокупность систем.
соответствует равносильная совокупность систем.
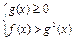 или
или 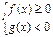
IV) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная совокупность систем.
соответствует равносильная совокупность систем.
 или
или 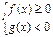
V) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная совокупность систем.
соответствует равносильная совокупность систем.
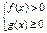 или
или 
VI) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная система.
соответствует равносильная система. 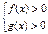
VII) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная совокупность систем.
соответствует равносильная совокупность систем.
 или
или 
VIII) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильная система.
соответствует равносильная система. 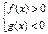
IX) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует равносильное неравенство
соответствует равносильное неравенство 
X) Неравенствах вида 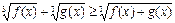 решаются следующим образом.
решаются следующим образом.
Неравенству 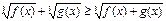 соответствует равносильное неравенство.
соответствует равносильное неравенство.
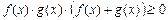
XI) Неравенствах вида  решаются следующим образом.
решаются следующим образом.
Неравенство 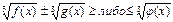 решается обобщенным методом интервалов.
решается обобщенным методом интервалов.
XII) Решение некоторых иррациональных уравнений можно свести к однородным уравнениям.
Например.
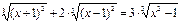
Пусть  ,
, 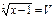 , тогда
, тогда

Пример №1.
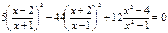
Введем замену: Пусть  ,
,  , тогда
, тогда
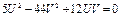
1) если 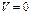 , тогда
, тогда  , тогда
, тогда 
2) Разделим обе части уравнения на 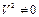 , получим
, получим

Пример №2.


Пусть  ,
,  , тогда
, тогда 
Найдем 
Составим систему: 
IV) Уравнения вида  , где
, где  эффективно решать перемножением
эффективно решать перемножением  и
и 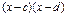 , а затем делать замену.
, а затем делать замену.
V) В уравнениях вида 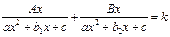 и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
VI) В уравнениях вида  обе части уравнения делятся на
обе части уравнения делятся на 
VII) Уравнения вида  и к ним сводящиеся решаются при помощи замены
и к ним сводящиеся решаются при помощи замены 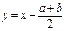
Методы решения неравенств, содержащих знак модуль.
I) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если 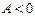 , то решений нет
, то решений нет
Если  , то
, то 
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
II) Неравенства вида 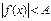 решаются следующим образом.
решаются следующим образом.
Если 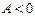 , то решений нет
, то решений нет
Если  , то решений нет
, то решений нет
Если  , то неравенству
, то неравенству 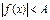 равносильна система
равносильна система 
III) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если 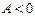 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 
Если  , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 
Если  , то неравенству
, то неравенству  равносильна совокупность
равносильна совокупность 
IV) Неравенства вида 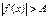 решаются следующим образом.
решаются следующим образом.
Если 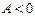 , то неравенство верно для любых х из области определения
, то неравенство верно для любых х из области определения 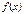
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 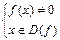
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 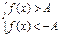
V) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству 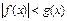 равносильна система
равносильна система 
VI) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то решений нет.
, то решений нет.
Если  , то неравенству
, то неравенству  соответствует уравнение
соответствует уравнение 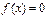
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
VII) Неравенства вида 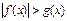 решаются следующим образом.
решаются следующим образом.
Если  , то неравенство
, то неравенство 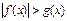 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенству
, то неравенству  равносильна система
равносильна система 
Если  , то неравенству
, то неравенству 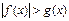 равносильна совокупность
равносильна совокупность 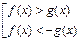
VIII) Неравенства вида  решаются следующим образом.
решаются следующим образом.
Если  , то неравенство
, то неравенство  верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенство
, то неравенство 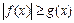 верно для любых значений x из области определения неравенства
верно для любых значений x из области определения неравенства 
Если  , то неравенству
, то неравенству 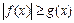 равносильна совокупность
равносильна совокупность 
IX) Неравенства вида  и
и  решаются следующим образом.
решаются следующим образом.
Неравенству  соответствует неравенство
соответствует неравенство 
Неравенству  соответствует неравенство
соответствует неравенство 
X) Решение неравенств используя определение модуля (общий способ).
P.S
Любое неравенство можно решит общим способом.

