
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Элементы статистической физики
Основные формулы 1. Распределение Больцмана (распределение частиц в силовом поле)
где п – концентрация частиц; U – их потенциальная энергия; п0 – концентрация частиц в точках поля, где U = 0; k – постоянная Больцмана; T – термодинамическая температура; е – основание натуральных логарифмов.
2. Барометрическая формула (распределение давления в однородном поле силы тяжести)
где р – давление газа; т – масса частицы; m – молярная масса; h – высота точки по отношению к уровню, принятому за нулевой; р0 – давление на этом уровне; g – ускорение свободного падения; R – универсальная газовая постоянная.
3. Вероятность того, что физическая величина х, характеризующая молекулу, лежит в интервале значений от х до х + dх, равна
где f (х) – функция распределения молекул по значениям данной физичес-кой величины х (плотность вероятности).
4. Количество молекул, для которых физическая величина х, характеризующая их, заключена в интервале значений от х до х + dх,
5. Распределение Максвелла (распределение молекул по скоростям) выражается двумя соотношениями: а) число молекул, скорости которых заключены в пределах от v до v + dv,
где f (v) – функция распределения молекул по абсолютным значениям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от v до v + dv, к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале; N – общее число молекул; т – масса молекулы; б) число молекул, относительные скорости которых заключены в пределах от и до и + dи,
где f (и) – функция распределения по относительным скоростям.
6. Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
где d – эффективный диаметр молекулы; п – концентрация молекул; ávñ – средняя арифметическая скорость молекул.
7. Средняя длина свободного пробега молекул газа
8. Импульс (количество движения), переносимый молекулами из одного слоя газа в другой через элемент поверхности,
где h – динамическая вязкость газа;
DS – площадь элемента поверхности; dt – время переноса.
9. Динамическая вязкость
где r – плотность газа (жидкости); ávñ – средняя скорость хаотического движения его молекул; álñ – их средняя длина свободного пробега.
10. Закон Ньютона
где F – сила внутреннего трения между движущимися слоями газа.
11. Закон Фурье
где DQ – теплота, прошедшая посредством теплопроводности через сечение площадью S – за время Dt; К – теплопроводность; dT/dx – градиент температуры. 12. Теплопроводность (коэффициент теплопроводности) газа
где сV – удельная теплоемкость газа при постоянном объеме; r – плотность газа; ávñ – средняя арифметическая скорость его молекулы; álñ – средняя длина свободного пробега молекул.
13. Закон Фука
где Dт – масса газа, перенесенная в результате диффузии через поверхность площадью S за время Dt; D – коэффициент диффузии; т1 – масса одной молекулы.
14. Коэффициент диффузии
Примеры решения задач
Задача 1. Какая часть молекул кислорода, находящегося при температуре Т = 300 °К, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше, чем на 4 м/с.
Решение
Закон распределения молекул по скоростям (закон Максвелла): число молекул DN, относительные скорости которых лежат в интервале от u до u + Du, равно
| |||||||
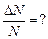
|
Здесь N – полное число молекул газа,
 – функция распределения Максвелла,
– функция распределения Максвелла,

где v – данная скорость;
vв – наиболее вероятная скорость.
Уравнение (1) справедливо при условии Du << u. По условию задачи v = vв, следовательно,  и уравнение (1) примет вид
и уравнение (1) примет вид

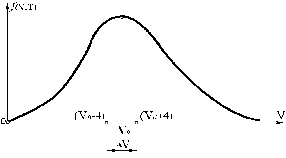
Сначала убедимся, что Du << u. Так как  то
то
 (2)
(2)
Определим теперь наиболее вероятную скорость
 м/с.
м/с.
Подставляя это значение vв в (2) и имея ввиду, что Dv = 8 м/с,
поскольку в задаче идет речь о скоростях, лежащих в интервале от
(vв – 4) м/с до (vв + 4) м/с, получим

т. е. Du << u.

Задача 2. Найти среднюю продолжительность свободного пробега молекул кислорода при давлении 2 мм рт. ст и температуре 27 °С.
| Дано: р = 2 мм рт. ст. = 266 Па Т = 300 °К m = 32 ·10–3 кг/моль s = 2,9 ·10–10 м (из таблицы) |
Решение
Средняя продолжительность свободного пробега молекул равна отношению
|
| t = ? |
где álñ – средняя длина свободного пробега молекул;
ávñ – средняя арифметическая скорость молекул.
Среднюю длину свободного пробега молекул газа можно вычислить по формуле

где s – эффективный диаметр молекул;
k – постоянная Больцмана.
Средняя арифметическая скорость молекул газа вычисляется по формуле

Тогда

Ответ: t = 9,3 ·10–8 с.
Задача 3. Пространство между двумя большими параллельными пластинами заполнено гелием. Расстояние между пластинами Dl = 50 мм. Одна пластина поддерживается при температуре Т1 = 293 °К, другая при температуре Т2 = 313 К. Вычислить поток тепла q, приходящейся на единицу площади пластин, если давление в газе 760 мм рт.ст.
| Дано: Dl = 5 ·10–2 м T1 = 293 °К T2 = 313 К р = 105 Па |
Решение Из закона Фурье количество теплоты, прошедшее посредством теплопроводности через площадь DS за время Dt, равно
|

|
Поток тепла представляет собой количество тепла, прошедшее через площадь DS за единицу времени, поэтому

Коэффициент теплопроводности

где r – плотность гелия;

Плотность гелия при данных условиях можно найти, пользуясь уравнением Менделеева–Клапейрона

откуда
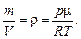
Подставив выражения для ávñ, álñ, cV и r выразим К:
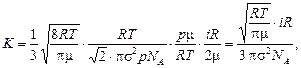
где 
Тогда поток тепла через единичную площадь будет равен
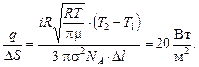
 |
Термодинамика
Последнее изменение этой страницы: 2019-03-22; Просмотров: 75; Нарушение авторского права страницы