Физические основы термодинамики ⇐ ПредыдущаяСтр 3 из 3   Основные формулы   1. Связь между молярной (Сm) и удельной (с) теплоемкостями газа   где m – молярная масса газа.   2. Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны     где i – число степеней свободы;  R – универсальная газовая постоянная.   3. Удельные теплоемкости при постоянном объеме и постоянном давлении соответственно равны:   .   4. Уравнение Р. Майера     5. Показатель адиабаты     6. Внутренняя энергия идеального газа     где áeñ – средняя кинетическая энергия молекулы;  N – число молекул газа;  n – количество вещества.  – изменение внутренней энергии.   7. Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле   где V1 – начальный объем газа;  V2 – его конечный объем. Работа газа при изобарическом процессе (р = const):     при изотермическом процессе (Т = const):     при адиабатическом процессе:     где Т1 – начальная температура газа;  Т2 – его конечная температура.   8. Уравнение Пуассона (уравнение газового состояния при адиабатическом процессе)     9. Связь между начальным и конечным значениями параметров состояний газа при адиабатическом процессе:     10. Первое начало термодинамики в общем случае записывается в виде   где Q – количество теплоты, сообщенное газу;  DU – изменение его внутренней энергии;  A – работа, совершаемая газом против внешних сил. Первое начало термодинамики при изобарическом процессе:     при изохорическом процессе (А = 0):     при адиабатическом процессе (Q = 0):     11. Термический коэффициент полезного действия (КПД) цикла в общем случае ,   где Q1 – количество теплоты, полученное рабочим телом (газом) от нагревателя;  Q2 – количество теплоты, переданное рабочим телом охладителю.   КПД цикла Карно   ,   где Т1 – температура нагревателя;  Т2 – температура охладителя.   12. Изменение энтропии     где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути.   13. Формула Больцмана     где S – энтропия системы;  W – термодинамическая вероятность ее состояния;  k – постоянная Больцмана.   Примеры решения задач   Задача 1. В вертикальном цилиндре под тяжелым поршнем находится кислород массой т = 1 кг. Для повышения температуры кислорода на DТ = 10 °К ему было сообщено количество теплоты Q = 9,1 кДж. Найти удельную теплоемкость кислорода, работу, совершаемую им при расширении, и увеличение его внутренней энергии.   Дано: m = 1 кг m = 32 ·10–3 кг/моль Q = 9,1·103 Дж DТ = 10 °К Решение   Так как поршень в любой момент находится в равновесии, то во время нагревания кислорода его давление р остается также постоянным. Тогда удельная теплоемкость при постоянном давлении

c р = ? А = ? DU = ?

 

Работа расширения при постоянном давлении

 

,

 

где V₁ и V₂ – начальный и конечный объем газа.

Уравнение состояния газа до и после нагревания     

 

                                          (1)

и

                                         (2)

 

Вычитая из выражения (2) выражение (1), найдем

 

следовательно,

 кДж.

 

Подводимое к газу количество теплоты идет на увеличение его внутренней энергии DU и на совершение работы А:

 

отсюда

 кДж.

 

Задача 2. В цилиндре с площадью основания 100 см² находится воздух при температуре 17° С. На высоте 50 см от основания цилиндра расположен легкий поршень, на котором лежит гиря весом 50 кГ. Какую работу совершит газ при расширении, если его нагреть на 50 °С? Атмосферное давление 760 мм рт. ст.

 

Дано: S = 100 см2 = 0,01 м2 Т1 = 290 °К h = 0,5 м Р0 = 150 кГ = 1470 Н рА = 760 мм рт. ст. = 1·105 Па DТ = 50 °К	Решение   В процессе нагревания газ расширяется и совершает работу по преодолению веса груза и силы атмосферного давления, действующих на поршень. Так как эти силы постоянны, то при достаточно медленном нагревании газ будет расширятся изобарически и его работу можно вычислить:
А = ?

 

 

При равновесии поршня давление р уравновешивается атмосферным давлением р_А и давлением, создаваемым гирей весом Р₀:

 

 

По закону Гей-Люссака ,

следовательно,

 Дж.

 

Задача 3. Азот, занимавший при давлении р₁ = 2 ·10⁵ Па объем
V₁ = 5 л, расширяют до объема 8 л, при этом давление падает до значения
р₂ = 10⁵ Па. Процесс происходит сначала по изотерме, затем – по изохоре. Определить работу сил давления газа, изменение внутренней энергии и количество поглощенной теплоты при этом переходе.

 

Дано: p1 = 2·105 Па V1 = 5 л = 5·10–3 м3 V2 = 8 л = 8·10–3 м3 m = 28·10–3 кг/моль р2 = 105 Па i = 5	Решение
Q12 = ? DU12 = ? А12 = ?

 

При переходе из состояния 1 в состояние 2 надо рассмотреть каждый из указанных процессов отдельно, тогда

 

                        (1)

 

Изменение внутренней энергии не зависит от процесса и в любом случае

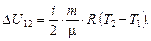                                 (2)

 

Используя уравнение Менделеева–Клапейрона для состояний 1 и 2, получим

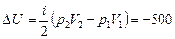 Дж.

 

Работа газа при изотермическом расширении

 

 Дж.

 

Учитывая, что А_{а 2} = 0, находим А₁₂ = А_1а = 470 Дж.

Для изотермического процесса (участок 1–а)

 

 Дж; .

 

Для изохорического процесса (участок а–2)

 

 Дж.

 

Общее количество теплоты

 

 Дж.

 

Знак минус показывает, что газ отдавал теплоту окружающим телам.

Задача 4. Некоторая масса азота при давлении 1 атм имела объем 5 л, а при давлении 3 атм – объем 2 л. Переход от начального к конечному состоянию был сделан в два этапа: сначала по изохоре, а затем по изобаре. Определить изменение внутренней энергии, количество теплоты и произведенную работу.

 

Дано: i = 5 р1 = 1 атм = 105 Па V1 = 5 л = 5·10–3 м3 р2 = 3 атм = 3·105 Па              V2 = 2 л = 2·10–3 м3 m = 32·10–3 кг/моль	Решение   Покажем графически, как происходил переход газа от первого состояния ко второму:
1) DU = ? 2) Q = ? 3) A = ?

 

1) При изохорном процессе вся теплота идет только на изменение внутренней энергии, работа при изохорном процессе не совершается, т. е.

 

 

 

2) При изобарном процессе на основе I начала термодинамики теплота идет как на изменение внутренней энергии, так и на работу:

 

 

 

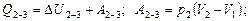
За оба процесса:

 

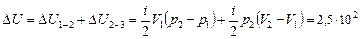 Дж,

 

 Дж,

 

 Дж.

 

Задача 5. Определить отношение  для смеси 3 молей аргона и 5 молей кислорода.

 

Дано:   n1 = 3 моля n2 = 5 молей m1 = 40·10–3 кг/моль m2 = 32·10–3 кг/моль i1 = 3 i2 = 5	Решение   По определению молярные теплоемкости и соответственно равны:
g = ?

 

Общее количество теплоты, затраченное на нагревание смеси из аргона и кислорода, найдем как сумму теплоты, затраченной на нагревание каждого газа в отдельности, а число молей смеси – как сумму молей аргона и кислорода, тогда

 

 

 

 

 

 

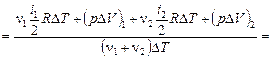
Ответ: 1,47.

 

Задача 6. Температура пара, поступающего в паровую машину,
t₁ = 130 °С; температура в конденсаторе t₂ = 25 °С. Определить теоретически максимальную работу при затрате количества теплоты Q = 5,1 кДж.

 

Дано: T1 = 403 °К Т2 = 298 °К Q1 = 5,1·103 Дж	Решение   Коэффициент полезного действия цикла Карно .                        (1)   КПД любого теплового двигателя
А = ?

,                           (2)

 

где А – полезная работа, совершаемая двигателем;

 Q₁ – количество теплоты, полученное рабочим телом от нагревателя.

Приравнивая правые части равенств (1) и (2), получим

 

откуда

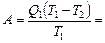1,3 кДж.

Задача 7. Кислород, масса которого т = 160 г при температуре
t₁ = 27 °С расширяется изотермически, а затем изохорно нагревается до
t₂ = 127 °С. Найти изменение энтропии, если известно, что начальное и конечное давления одинаковы.

 

Дано: т = 1,16 кг m = 32·10–3 кг/моль i = 5 Т1 = 300 °К Т2 = 400 °К	Решение
S3 – S1 = ?

 

Для процессов 1–2–3 изменение энтропии

 

                                 (1)

 

где

 

Подставляя выражения dQ_T и dQ_V в выражение (1) и учитывая, что при изотермическом процессе  получим:

 

 

Учитывая, что р₁ / р₂ = V₂ / V₁ (для процесса 1–2) и р₁ / р₂ = T₂ / T₁ (для процесса 2–3), получим V₂ / V₁ = T₂ / T₁, тогда

 

 

Задача 8 . 14 г азота адиабатически расширяются так, что давление уменьшается в 5 раз, а затем изотермически сжимаются до первоначального давления. Найти приращение энтропии при этих процессах.

 

Дано: d Q1 = 0 т = 1,4·10–4 кг m = 28·10–3 кг/моль р1/р2 = 5 Т2 = соnst	Решение   Приращение энтропии можно найти по формулам
DS = ?

 

где ΔS₁ – приращение энтропии при адиабатическом процессе;

 ΔS₂ – приращение энтропии при изотермическом процессе.  

Так как dQ₁ = 0 по условию задачи, то и ΔS₁ = 0. Чтобы найти ΔS₂ запишем, чему равно количество теплоты dQ₂, которое при изотермическом процессе полностью расходуется на работу, т. е. dQ₂ = pdV. Отсюда  Используя уравнение Менделеева-Клапейрона выразим давление через температуру и объем и подставим вместо р под интеграл. Тогда

 

 

Задача 9. Найти приращение энтропии DS при расширении 2 г водорода от V₁ = 1,5 л до V₂ = 4,5 л, если процесс расширения происходит: 1) при постоянном давлении; 2) при постоянной температуре.

 

Дано: i = 5 т = 2·10–3 кг m = 2·10-3 кг/моль V1 = 1,5·10–3 м3 V2 = 4,5·10–3 м3 1) р = соnst 2) Т = соnst	Решение   Используя формулу для приращения энтропии , найдем  и , выразив dQ из I начала термодинамики сначала для изобарического, а затем для изотермического процессов:
DS1 = ? DS2 = ?

1)

 

 

Отношение  при изобарическом процессе равно отношению  поэтому

 

 

2)

 

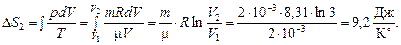
РЕАЛЬНЫЕ ГАЗЫ. ЖИДКОСТИ

 

Основные формулы

1. Уравнение Ван-дер-Ваальса для одного моля газа

 

 

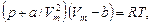
для произвольного количества вещества n газа

 

 

где a и b – постоянные Ван-дер-Ваальса (рассчитанные на один моль газа);

 V – объем, занимаемый газом; V_m – молярный объем;

 р – давление газа на стенки сосуда;

или  – внутренне давление, обусловленное силами взаимодействия молекул.

 

2. Связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:

 

 

3. Внутренняя энергия реального газа

 

 

где С _V – молярная теплоемкость газа при постоянном объеме.

 

4. Поверхностное натяжение

 

 

где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости, или

 

 

где DЕ – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.

 

5. Формула Лапласа в общем случае записывается в виде

 

где р – давление, создаваемое изогнутой поверхностью жидкости;

 s – поверхностное натяжение;

 R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости, а в случае сферической поверхности

 

 

6. Высота подъема жидкости в капиллярной трубке

 

 

где q – краевой угол;

 R – радиус канала трубки;

 r – плотность жидкости;

 g – ускорение свободного падения.

 

7. Высота подъема жидкости между двумя близкими и параллельными плоскостями

 

 

где d – расстояние между плоскостями.

 

8. Расход жидкости в трубке тока:

а) объемный расход Q_V = vS;

б) массовый расход Q_m = rvS, где S – площадь поперечного сечения трубки тока; v – скорость жидкости; r – ее плотность.

 

9. Уравнение неразрывности струи

 

где S₁ и S₂ – площади поперечного сечения трубки тока в двух местах;

 v₁ и v₂ – соответствующие скорости течений.

 

10. Уравнение Бернулли для идеальной несжимаемой жидкости в общем случае

 

где р₁ и р₂ – статические давления жидкости в двух сечениях трубки тока;

 v₁ и v₂ – скорости жидкости в этих сечениях;

 и  – динамические давления жидкости в этих же сечениях;

 h₁ и h₂ – высоты сечений над некоторым уровнем;

 rgh₁ и rgh₂ – гидростатические давления.

Уравнения Бернулли в случае, когда оба сечения находятся на одной высоте (h₁ = h₂),

 

11. Скорость течения жидкости из малого отверстия в открытом широком сосуде

 

где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде.

 

Примеры решения задач

 

Задача 1. Бак, имеющий форму куба, длина ребра которого l, наполнен водой. определить силу давления на стенку бака со стороны воды, если атмосферное давление равно р₀.

 

Дано:   l, r, p0

Решение

 

  F = ?

 

На рисунке показан график зависимости давления от глубины погружения h. Давление на боковую стенку линейно зависит от h, следовательно,

 

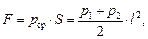
где р₁ = р₀; р₂ = р₀ + rgl.

 

Таким образом,

 

Ясно, что сила давления не будет приложена в центре грани куба, а будет несколько смещена вниз.

Задача 2. Полный медный шар, наружный объем которого V, плавает в воде так, что половина его погружена в воду. Найти объем полости шара, если плотность меди r₁, а воды – r₂.

 

Дано:   r1; r2; V	Решение
V0 = ?

 

Так как шар находится в равновесии, то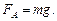

 

Масса шара m = r₁ (V – V₀).

По закону Архимеда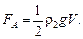

Получим уравнение

 

откуда

 

Задача 3. Найти добавочное давление, обусловленное поверхностным натяжением, внутри шаровой капли радиусом R. Коэффициент поверхностного натяжения жидкости равен s.

 

Дано:   s; R	Решение   Рассечем мысленно каплю диаметральной плоскостью на две половинки. Вследствие поверхностного натяжения обе половинки притягиваются друг к другу с силой  Эта сила прижимает друг к другу оба полушария по поверхности S = pR2, поэтому
Dр = ?

Задача 4. Найти массу воды, поднявшейся по стеклянной капиллярной трубке диаметром 0,5 мм, если коэффициент поверхностного натяжения воды 7,2 ·10^–2 Н/м.

 

Дано:   s = 7,2 ·10–2 Н/м d = 0,5 ·10–3 м	Решение   Сила поверхностного натяжения, действующая по краю мениска жидкости, направлена вверх и уравновешивает силу тяжести столбика жидкости.
т = ?

 

откуда

 кг.

 

Задача 5. Из трубы сечением S₁ бьет вертикально вверх струя воды. Найти сечение струи на высоте h над отверстием трубы. Расход воды из трубы равен Q.

 

Дано:   S1; h; Q	Решение   Уравнение Бернулли для данного случая:
S2 = ?

 

где v₁ – скорость воды в сечении S₁;

 v₂ – скорость в сечении струи S₂ на высоте h.

Уравнение неразрывности

 

 

Отсюда находим v₁ и v₂ и подставляем в уравнение Бернулли:

 

откуда

 

КОНТРОЛЬНАЯ РАБОТА № 2

 

Студент-заочник должен решить семь задач того варианта, номер которого совпадает с третьей цифрой справа его шифра.

Пример. Номер шифра (номер зачетной книжки) 13799. Студент решает седьмой вариант.

 

Вариант	Номера задач
0	3	15	21	34	42	53	62
1	7	12	27	40	44	58	65
2	5	19	30	33	48	51	67
3	10	16	22	35	46	59	61
4	6	11	26	38	43	54	64
5	8	20	29	31	49	56	68
6	1	14	23	36	47	60	69
7	9	17	25	37	45	52	63
8	4	13	24	32	50	57	66
9	2	18	28	39	41	55	70

 

1. Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины останется в трубке столбик ртути? Атмосферное давление равно
750 мм рт. ст.

 

2. Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути высотой h = 20 см. если трубку поставить вертикально, столбик ртути сместится на l = 10 см. до какого давления была откачана трубка? Плотность ртути r = 1,36 ·10⁴ кг/м³.

 

3. Два баллона соединены трубкой с краном. В первом находится газ при давлении 10⁵ Па, во втором – при давлении 0,6 ·10⁵ Па. Объем первого баллона V₁ = 1 л, второго – V₂ = 3 л. какое давление установится в баллонах, если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.

 

4. Три баллона емкостью V₁ = 3 л, V₂ = 7 л и V₃ = 5 л наполнены соответственно кислородом (р₁ = 2 ·10⁵ Па), азотом (р₂ = 3 ·10⁵ Па) и углекислым газом (р₃ = 0,6 ·10⁵ Па) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?

 

5. Дан график изменения состояния идеального газа в координатах р, V. Представить этот цикл в координатах р, T и V, Т.

 

 

6. В цилиндре, площадь основания которого равна S = 100 см², находится воздух при температуре 12 °С. атмосферное давление 10⁵ Па. На высоте h = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой т = 100 кг, а воздух в цилиндре при этом нагреть до 27 °С? трение поршня о стенки цилиндра и вес самого поршня не учитывать.

 

7. Из баллона со сжатым водородом емкостью V = 10 л вследствие неисправности вентиля утекает газ. При температуре t₁ = 7 °С манометр показывал р = 5 ·10⁶ па. Через некоторое время при температуре t₂ = 17 °С манометр показал такое же давление. Сколько утекло газа?

 

8. Сколько молекул воздуха выходит из комнаты объемом V₀ = 120 м³ при повышении температуры от t₁ = 15 °С до t₂ = 25 °С? Атмосферное давление р₀ = 10⁵ Па.

 

9. При какой температуре кислород (О₂), находясь под давлением 0,2 ·10⁶ па, имеет плотность 1,2 кг/м³?

 

10. В сосуде при температуре t = 100 °С и давлении р = 4 ·10⁵ Па находится 2 м³ смеси кислорода О₂ и сернистого газа SO₂. Определить парциальное давление компонентов, если масса сернистого газа 8 кг.

 

11. В баллоне емкостью 0,05 м³ находятся 0,12 кмоль газа при давлении 0,6 ·10⁷ Па. Определить среднюю кинетическую энергию теплового движения молекул газа.

 

12. Найти средние квадратичные скорости молекул азота и кислорода при температуре 27 °С.

 

13. Найти импульс молекулы водорода при температуре 20 °С. скорость молекулы считать равной средней квадратичной скорости.

 

14. В сосуде объемом 5 л находится 20 г кислорода под давлением 10⁵ Па. Найти: 1) среднюю квадратичную скорость молекул газа; 2) число молекул, находящихся в сосуде; 3) плотность газа.

 

15. Средняя квадратичная скорость молекул некоторого газа равна
500 м/с. Давление газа равно 5 ·10⁴ Па. Найти плотность газа при этих условиях.

 

16. Средняя квадратичная скорость молекул некоторого газа при нормальных условиях равна 461 м/с. Какое количество молекул содержится в 1 г этого газа?

 

17. Чему равна энергия вращательного движения молекул, содержащихся в 1 кг азота при температуре 7 °С?

 

18. Чему равна энергия теплового движения молекул двухатомного газа, заключенного в сосуд объемом 2 л и находящегося под давлением в 1,5 ·10⁵ Па?

 

19. 1 кг двухатомного газа находится под давлением 8·10⁴ па и имеет плотность 4 кг/м³. Найти энергию теплового движения молекул газа при этих условиях.

 

20. Какое число молекул двухатомного газа занимает объем V = 10 см³ при давлении 40 мм рт. ст. и при температуре 27 °С? Какой энергией теплового движения обладают эти молекулы?

 

21. Кинетическая энергия поступательного движения молекул азота, находящегося в баллоне объемом 0,02 м³, равна 5 ·10³ Дж, а средняя квадратичная скорость его молекул равна 2 ·10³ м/с. Найти: 1) количество азота в баллоне; 2) давление, под которым находится азот.

 

22. Смесь состоит из двух молей одноатомного газа и одного моля двухатомного газа. Определить мольные теплоемкости  и 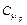смеси.

 

23. Вычислить теплоемкость при постоянном объеме двухатомного газа, заключенного в сосуд V = 10 л при нормальных условиях.

 

24. Разность удельных теплоемкостей некоторого двухатомного газа с_р – с _V = 2,08 кДж/кг ·К. Определить молярную массу m газа и его удельные теплоемкости с_р и с _V.

 

25. Каковы удельные теплоемкости с_р и с _V смеси газов, содержащей кислород массой т₁ = 10 г и азот массой т₂ = 20 г?

 

26. Определить удельную теплоемкость с _V смеси газов, содержащей V₁ = 5 л водорода и V₂ = 3 л гелия. Газы находятся при одинаковых условиях.

 

27. В баллоне находятся аргон и азот. Определить удельную теплоемкость с _V смеси газов, если массовые доли аргона и азота одинаковы и равны 0,5.

 

28. Вычислить удельные теплоемкости с_р и с_V газов: 1) гелия; 2) углекислого газа.

 

29. Для некоторого двухатомного газа удельная теплоемкость при постоянном давлении равна 840 Дж/кг · К. чему равна масса одного моля этого газа?

 

30. Чему равны удельные теплоемкости с_р и с_V некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна 1,43 кг/м³?

 

31. Найти среднюю длину свободного пробега молекул азота при температуре 17 °С и давлении 10⁴ Па.

 

32. Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия 2,1 ·10^–2 кг/м³.

 

33. Найти среднее число столкновений в 1 с молекул азота при
t = 27 °С и давлении р = 0,5 ·10⁵ Па.

 

34. Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Диаметр молекул воздуха условно принять равным 3 ·10^–10 м.

 

35. В колбе объемом 100 см³ находится 0,5 г азота. Найти среднюю длину свободного пробега молекул азота при этих условиях.

 

36. Найти коэффициент внутреннего трения азота при нормальных условиях, если коэффициент диффузии для него при этих условиях равен 0,142 см²/с.

 

37. Найти диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего трения при 0 °С равен 18,8 ·10^–6 Н·с/м²?

 

38. Найти коэффициент диффузии и коэффициент внутреннего трения воздуха при давлении 10⁵ Па и температуре 10 °С. диаметр молекулы воздуха принять равным 3 ·10^–10 м.

 

39. Найти коэффициент диффузии гелия при нормальных условиях.

 

40. Какая часть молекул водорода при температуре 0 °С обладает скоростями от 2000 м/с до 2100 м/с.

 

41. Один киломоль воздуха при давлении р₁ = 10⁶ Па и температуре Т₁ = 390 °К изохорически изменяет давление так, что его внутренняя энергия изменяется на DU = –71,7 кДж, затем изобарически расширяется и совершает работу А = 745 кДж. Определить параметры воздуха (считать
с_V = 721 Дж/кг ·К = const).

 

42. При изобарическом сжатии азота была совершена работа, равная 12 кДж. Определить затраченное количество теплоты и изменение внутренней энергии газа.

 

43. Определить работу расширения 7 кг водорода при постоянном давлении и количество теплоты, переданное водороду, если в процессе нагревания температура газа повысилась на 200 °С.

 

44. В цилиндре диаметром 20 см и высотой 42 см с подвижным поршнем находится газ под давлением 12 ·10⁵ Па при температуре 300 °С. определить работу, совершаемую газом при снижении температуры до
10 °С при постоянном давлении.

 

45. При изотермическом сжатии 2,8 кг окиси углерода объем его уменьшился в четыре раза. Определить работу сжатия, если температура газа 7 °С.

 

46. Азот, адиабатически расширяясь, совершает работу, равную
480 кДж. Определить конечную температуру газа, если до расширения он имел температуру Т₁ = 362 К. масса азота т = 12 кг. Теплоемкость считать постоянной.

 

47. 28 г азота, находящегося при температуре 40 °С и давлении 10⁵ Па, сжимается до объема в 13 л. Найти температуру и давление азота после сжатия, если: 1) азот сжимается изотермически; 2) азот сжимается адиабатически. Найти работу сжатия в каждом из этих случаев.

 

48. При изотермическом расширении 2 кг водорода, взятых при давлении 6 ·10⁵ Па и объеме 8,31 м³, была совершена работа 547 ·10³ Дж. Определить конечные параметры водорода, если после изотермического расширения газ был адиабатически сжат, причем была совершена такая же работа, что и при расширении.

 

49. Сероводород (Н₂S) массой 6 кг, занимающий объем 3 м³ при температуре 27 °С, сжали адиабатически так, что давление его увеличилось в два раза. Определить конечные объем, температуру и изменение внутренней энергии газа.

 

50. Азот массой 2 кг при температуре 7 °С занимает объем 830 дм³. В конце адиабатического сжатия температура возросла до 227 °С, а давление увеличилось до 15,2 ·10⁵ Па. Определить отношение с_р /с_V.

 

51. Найти изменение энтропии при превращении 20 г льда при
t = –10 °С в пар при t = 100 °С.

 

52. Найти изменение энтропии при плавлении 1 кг льда, находящегося при температуре 0 °С.

 

53. Смешали воду массой 4 кг при температуре Т₁ = 280 К с водой массой 10 кг при температуре Т₂ = 350 К. Найти: 1) температуру смеси;
2) изменение энтропии, происходящее при смешивании.

 

54. Лед массой 2 кг при температуре 0 °С был превращен в воду той же температуры с помощью пара, имеющего температуру 100 °С. определить массу т₂ израсходованного пара. Каково изменение энтропии системы лед – пар?

 

55. 7 г водорода расширяются изобарически до удвоения объема. Найти изменение энтропии при этом расширении.

 

56. Найти изменение энтропии при изотермическом расширении 10 г водорода от 10⁵ до 0,5 ·10⁵ Па.

 

57. 650 г расплавленного свинца при температуре плавления вылили на лед при t = 0 °С. найти изменение энтропии при этом процессе.

 

58. Найти изменение энтропии при изобарическом расширении 15 г гелия от объема V₁ = 10 л до V₂ = 30 л.

 

59. Совершая цикл Карно, газ получил от нагревателя теплоту
Q₁ = 1 кДж и совершил работу А = 200 Дж. Температура нагревателя
Т₁ = 375 К. Определить температуру охладителя.

 

60. Совершая цикл Карно, газ отдал охладителю 2/3 теплоты, полученной от нагревателя. Определить температуру охладителя, если температура нагревателя Т₁ = 425 °К.

 

61. Какую работу А нужно совершить, чтобы, выдувая мыльный пузырь, увеличить его диаметр от d₁ = 1 см до d₂ = 11 см.

 

62. В воду опущена на очень малую глубину стеклянная трубка с диаметром внутреннего канала d = 1 мм. Найти массу вошедшей в трубку воды. Считать смачивание полным.

 

63. Определить работу А, которую необходимо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от V₁ = 10 см³ до
V₂ = 20 см³.

 

64. Две капли ртути радиусом R = 1 мм каждая слились в одну большую каплю без изменения температуры. Какая энергия выделится при этом слиянии?

 

65. Найти добавочное давление внутри мыльного пузыря диаметром 5 см. Определить также работу, которую нужно совершить, чтобы выдуть этот пузырь.

 

66. На сколько давление р воздуха внутри мыльного пузыря больше атмосферного давления р₀, если диаметр пузыря d = 5 мм?

 

67. Глицерин поднялся в капиллярной трубке на высоту h = 20 мм. Определить коэффициент поверхностного натяжения глицерина, если диаметр канала равен 1 мм.

 

68. Найти скорость течения по трубке углекислого газа, если известно, что за полчаса через поперечное сечение трубы протекает 0,51 кг газа. Плотность газа принять равной 7,5 кг/м³. Диаметр трубы равен 2 см.

 

69. Тонкое алюминиевое кольцо радиусом 8,0 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 10 г.

 

70. Под каким давлением находится воздух внутри пузырька радиусом 5 ·10^–3 мм, расположенного под поверхностью воды?

Литература

1. Зисман Г. А., Тодес О. М. Курс физики. – М.: Наука, 1970. –
Т. 1. – §§ 10, 11.

2. Савельев И. В. Курс общей физики. М.: Наука, 1977. – Т. 1. –
§§ 34–42.

3. Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. – М.: Высш. шк., 1973. – Т. 1. – §§ 4.1–4.3.

4. Чертов А. Г., Воробьев А. А. Задачник по физике. – М.: Высш. шк., 1981.

5. Новодворская Е. М., Дмитриев Э. М. Методика проведения упражнений по физике во втузе. – М.: Высш. шк., 1981. 

6. Беликов С. Б. Решение задач по физике. – М.: Высш. шк., 1986.

7. Савельев И. В. Сборник вопросов и задач по общей физике. – М.: Наука, 1987.

8. Трофимова Т. И. Курс физики. – М.: Высш. шк., 1994.

9. Трофимова Т. И., Павлова З. Г. Сборник задач по курсу физики с решениями. – М.: Высш. шк., 1999.

10. Айзенцон А. Е. Курс физики. – М.: Высш. шк., 1996. 

 

Справочные таблицы

 

⇐ Предыдущая123

Поделиться: