Производная сложной функции



Таблица производных
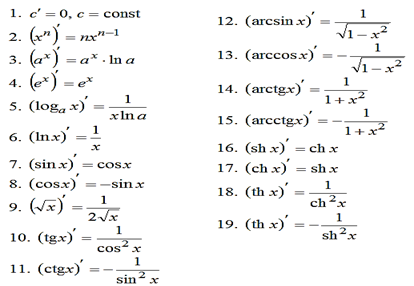
Теорема о возрастании и убывании функции
Теорема.
1) Если функция 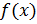 имеющая производную на отрезке
имеющая производную на отрезке 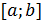 возрастает
возрастает
на этом отрезке, то ее производная на этом отрезке не отрицательна, т.е. 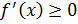
2) Если функция  непрерывна на отрезке
непрерывна на отрезке 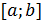 и дифференцируема на
и дифференцируема на
в промежутке 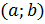 , причем
, причем  то эта функция возрастает на отрезке
то эта функция возрастает на отрезке 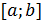 .
.
Доказательство. Докажем сначала первую часть теоремы. Пусть 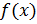 возрастает на отрезке
возрастает на отрезке 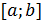 . Придадим аргументу х приращение
. Придадим аргументу х приращение 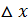 и рассмотрим отношение
и рассмотрим отношение 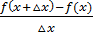
Так как 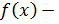 функция возрастающая, то
функция возрастающая, то 
В обоих случаях  , а следовательно,
, а следовательно,
 , т.е.
, т.е. 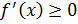 чтд.
чтд.
Докажем вторую часть теоремы. Пусть 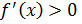 при всех значениях х, принадлежащих промежутку
при всех значениях х, принадлежащих промежутку 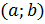 .
.
Рассмотрим два любых значения 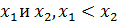 принадлежащих отрезку
принадлежащих отрезку 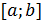
По теореме Лагранжа о конечных приращениях имеем 
По условию  следовательно,
следовательно,  – возрастающая функция.
– возрастающая функция.
Теорема о локальном максимуме и минимуме
Функции
Точка 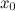 называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство: 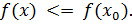
Точка 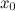 называется точкой локального минимума функции
называется точкой локального минимума функции  , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство: 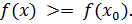
Теорема Ролля
Теорема. Теорема Ролля утверждает, что любая действительная дифференцируемая функция, принимающая одинаковые значения на концах интервала, должна иметь в этом интервале хотя бы одну стационарную точку, т.е. точку, в которой первая производная равна нулю.
В современной математике доказательство теоремы Ролля основывается на двух других теоремах − второй теореме Вейерштрасса и теореме Ферма. Они формулируются таким образом:
Вторая теорема Вейерштрасса. Если функция 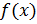 непрерывна на отрезке
непрерывна на отрезке 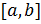 , то она достигает на нем своей точной верхней и нижней грани (т.е. наибольшего и наименьшего значения).
, то она достигает на нем своей точной верхней и нижней грани (т.е. наибольшего и наименьшего значения).
Теорема Ферма. Пусть функция 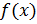 определена в окрестности точки
определена в окрестности точки 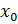 и дифференцируема в этой точке. Тогда, если функция
и дифференцируема в этой точке. Тогда, если функция 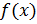 имеет локальный экстремум в точке
имеет локальный экстремум в точке 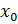 , то
, то  . Рассмотрим теперь теорему Ролля (или теорему о нуле производной) в более строгом изложении. Пусть функция
. Рассмотрим теперь теорему Ролля (или теорему о нуле производной) в более строгом изложении. Пусть функция 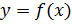 непрерывна на отрезке
непрерывна на отрезке 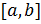 , дифференцируема на интервале
, дифференцируема на интервале  и принимает одинаковые значения на концах данного отрезка:
и принимает одинаковые значения на концах данного отрезка:  . Тогда на интервале
. Тогда на интервале  существует по крайней мере одна точка
существует по крайней мере одна точка  , в которой производная функции
, в которой производная функции 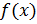 равна нулю:
равна нулю:  .
.
Доказательство. Если функция  постоянна на отрезке
постоянна на отрезке 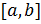 , то производная равна нулю в любой точке интервала
, то производная равна нулю в любой точке интервала  , т.е. в этом случае утверждение справедливо.
, т.е. в этом случае утверждение справедливо.
Если функция 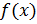 не является постоянной на отрезке
не является постоянной на отрезке 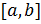 , то по теореме Вейерштрасса она достигает своего наибольшего или наименьшего значения в некоторой точке
, то по теореме Вейерштрасса она достигает своего наибольшего или наименьшего значения в некоторой точке  интервала
интервала  , т.е. в точке
, т.е. в точке  существует локальный экстремум. Тогда по теореме Ферма производная в этой точке равна нулю:
существует локальный экстремум. Тогда по теореме Ферма производная в этой точке равна нулю: 
Теорема Лагранжа
Теорема Лагранжа о среднем значении утверждает, что если функция 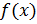 непрерывна на отрезке
непрерывна на отрезке 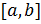 и дифференцируема на интервале
и дифференцируема на интервале  , то в этом интервале существует хотя бы одна точка
, то в этом интервале существует хотя бы одна точка  , такая, что
, такая, что 
Доказательство. Рассмотрим вспомогательную функцию 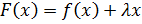 . Выберем число
. Выберем число  таким, чтобы выполнялось условие
таким, чтобы выполнялось условие  . Тогда
. Тогда  . В результате получаем
. В результате получаем  . Функция
. Функция  непрерывна на отрезке
непрерывна на отрезке 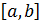 , дифференцируема на интервале
, дифференцируема на интервале  и принимает одинаковые значения на концах интервала. Следовательно, для нее выполнены все условия теоремы Ролля. Тогда в интервале
и принимает одинаковые значения на концах интервала. Следовательно, для нее выполнены все условия теоремы Ролля. Тогда в интервале  существует точка
существует точка  , такая, что
, такая, что
 . Отсюда следует, что
. Отсюда следует, что 
 . Теорема Лагранжа имеет простой геометрический смысл. Хорда, проходящая через точки графика, соответствующие концам отрезка a и b, имеет угловой коэффициент, равный
. Теорема Лагранжа имеет простой геометрический смысл. Хорда, проходящая через точки графика, соответствующие концам отрезка a и b, имеет угловой коэффициент, равный  . Тогда внутри отрезка
. Тогда внутри отрезка 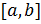 существует точка
существует точка  , в которой касательная к графику функции параллельна хорде.
, в которой касательная к графику функции параллельна хорде.
Теорема Коши
Теорема Коши о среднем значении обобщает формулу конечных приращений Лагранжа. В этой теореме устанавливается связь между производными двух функций и изменением этих функций на конечном отрезке.
Пусть функции 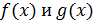 непрерывны на отрезке
непрерывны на отрезке 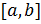 и дифференцируемы на интервале
и дифференцируемы на интервале  , причем
, причем 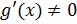 при всех
при всех  . Тогда в этом интервале существует точка
. Тогда в этом интервале существует точка  , такая, что
, такая, что 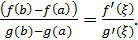
Доказательство. Прежде всего, заметим, что знаменатель в левой части формулы Коши не равен нулю:  . Действительно, если
. Действительно, если  , то по теореме Ролля найдется точка
, то по теореме Ролля найдется точка  , в которой
, в которой  . Это, однако, противоречит условию, где указано, что
. Это, однако, противоречит условию, где указано, что 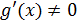 при всех
при всех  .
.
Введем вспомогательную функцию  . Выберем число
. Выберем число  таким образом, чтобы выполнялось условие
таким образом, чтобы выполнялось условие  . В этом случае получаем
. В этом случае получаем  . и функция
. и функция  принимает вид
принимает вид  . Эта функция непрерывна на отрезке
. Эта функция непрерывна на отрезке 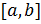 , дифференцируема на открытом интервале
, дифференцируема на открытом интервале  , и при найденном значении
, и при найденном значении  принимает одинаковые значения на границах интервала. Тогда по теореме Ролля в интервале
принимает одинаковые значения на границах интервала. Тогда по теореме Ролля в интервале  существует точка
существует точка  такая, что
такая, что  . Следовательно,
. Следовательно,  или
или  . Полагая
. Полагая  , из формулы Коши можно получить формулу Лагранжа:
, из формулы Коши можно получить формулу Лагранжа: 
Правило Лопиталя
Правило Лопиталя говорит, что если функции 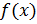 и
и 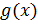 обладают следующим набором условий:
обладают следующим набором условий:
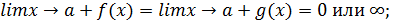
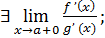
 в некоторой окрестности точки a,
в некоторой окрестности точки a,
тогда существует 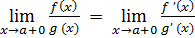
Докажем теорему для неопределённостей вида (0/0). 
Так как  , то по теореме Коши
, то по теореме Коши  , где
, где  .
.
Поскольку существует  который равен
который равен 
то существует и предел  , причем
, причем 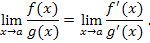
Докажем теорему для неопределённостей вида (∞/∞).
Функции 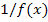 и
и  являются бесконечно малыми при
являются бесконечно малыми при  . Тогда
. Тогда
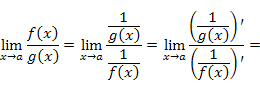


Следовательно,


