
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Морозов Ю.Д., Лейбенко В.Г.Стр 1 из 6Следующая ⇒
Проектирование деталей машин: учебное пособие. – М.: МГУПИ, 2012. 48 с.
В пособии изложена инженерная методика проектирования конструкций машин на примерах разработки приводов конвейера в курсовом проекте по деталям машин, включая обоснование материалов и размеров основных деталей и методику конструирования приводов. Представлены варианты конструкций приводов, их узлов и деталей и примеры оформления технической документации на стадиях эскизного, технического и рабочего проектов. Предназначено студентам, изучающим курс «Детали машин и основы конструирования» по кафедре «Прикладная механика».
Табл.: 50. Ил.: 53. Библиограф.: 4 назв.
- 3 -
СОДЕРЖАНИЕ
Основные обозначения и принятые размерности P – мощность, кВт ( P1 - на ведущем элементе передачи, P2 - на ведомом ); Т – крутящий момент, Нм (Т1 - на ведущем элементе передачи, Т2 - на ведомом); n - частота вращения, об/мин ( n1 - ведущего элемента передачи, n2 - ведомого ); u - передаточное число; η - коэффициент полезного действия; F – сила, Н ( Ft - окружная, Fr - радиальная, Fa – осевая ); σ и [σ ] – нормальное напряжение расчетное и допускаемое, МПа (σ H - контактное, σ F – изгиба зубьев); p - давление, МПа; v - скорость, м/с; a – межосевое расстояние, мм; d – диаметр, мм (d1 - делительный ведущего элемента передачи, d2 – … ведомого); m – модуль зацепления, мм; Lh - ресурс, час; Обозначения со знаком ' (штрих) - предварительно обоснованные, ожидаемые характеристики. Прочие обозначения пояснены в тексте.
- 4 - 1. Задания* на курсовое проектирование по ДМ Спроектировать привод конвейера по заданным кинематической схеме и параметрам, предназначенный для работы в закрытом отапливаемом помещении с единичными перегрузками Кп=Тмах/Тном=1, 5. Производство приводов серийное.
5 6 7 8
В А Р И А Н Т Ы | ||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||||||
| P ВЫХ, кВт | 2 | 2, 2 | 2, 4 | 2, 6 | 2, 8 | 3, 2 | 3, 6 | 4 | 4, 5 | 5 | 5, 6 | 6, 3 | 7, 1 | 8 | 9 | 10 | 11 | |||||
| u | 2, 8 | 3, 15 | 3, 55 | 4 | 4, 5 | 5 | 5, 6 | 6, 3 | 8 | 14 | 16 | 18 | 20 | 25 | 28 | 31, 5 | 35, 5 | |||||
| n С, об/мин | 750 | 1000 | 1500 | 3000 |
| |||||||||||||||||
| Варианты | θ 1 | λ 1 | θ 2 | λ 2 | θ 3 | λ 3 | Lh, час |
| 1 | 1 | 1 | - | - | - | - | 8000 |
| 2 | 1 | 0, 1 | 0, 8 | 0, 9 | - | - | 10000 |
| 3 | 1 | 0, 1 | 0, 9 | 0, 3 | 0, 7 | 0, 6 | 12000 |
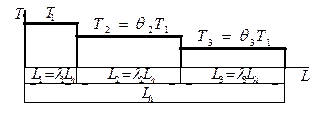
 График нагружения ……………………………….
График нагружения ……………………………….
.
* № задания состоит из номеров вариантов: кинематической схемы, PВЫХ , u, n С, графика нагружения.
Пример оформления 1. Техническое задание (по варианту № 5.13.10.3.2)
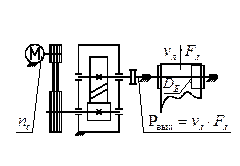 Спроектировать привод конвейера по схеме - рис. 1.1 с указанными ниже характеристиками и графиком нагружения - рис.1.2, предназначенный для работы в закрытом отапливаемом помещении.
Спроектировать привод конвейера по схеме - рис. 1.1 с указанными ниже характеристиками и графиком нагружения - рис.1.2, предназначенный для работы в закрытом отапливаемом помещении.
 PВЫХ=7, 1 кВт– мощность на выходном
PВЫХ=7, 1 кВт– мощность на выходном
валу привода;
u=14 – передаточное число привода;
nС=1500 об/мин – синхронная частота
двигателя;
Kп=1, 5 – коэффициент единичных
перегрузок;
Lh=10000 час – ресурс привода. Рис. 1.1 Рис. 1.2
- 5 -
2. Энергосиловой и кинематический расчеты привода
Исходные данные*: кинематическая схема (например, рис. 1.1); Pвых; u; nс.
Цель расчета - определение характеристик валов Pi, ni, Ti (здесь i - порядковый номер вала), для передач и муфт ui, η i (i - номер ведомого вала передачи или муфты, см. рис.2.1).
Для этого принять КПД передач η i привода согласно рекомендаций (табл. 2.1), и определить общий КПД привода η ПР= η 1·η 2·η 3… и мощности на валах Pi-1= Pi / η i.
 Таблица2.1
Таблица2.1
|
Тип передачи |
КПД одной ступени | U * РЕКОМЕНДУЕМОЕ (UМАХ) | |
| закрытая | открытая | ||
| Зубчатая: цилиндрическая коническая | 0, 97 0, 96 | 0, 96 0, 95 | 2…6, 3 (7, 1) 2…4 (6, 3) |
| Червячная | ≈ 1- u /200 | - | 8…60 (80) |
| Цепная | 0, 95 | 0, 93 | 1, 5…5 (10) |
| Клиноременная | - | 0, 95 | 1, 5…4 (8) |
| Муфта | 0, 98 … 0, 99 | 1 | |
Рис. 2.1
Выбрать стандартный электродвигатель (см. приложение 1) с номинальной мощностью PЭ≥ P0/1, 05= =PВЫХ /η ПР/ 1, 05 (допуская его перегрузку до 5%) и номинальной частотой вращения nЭ≈ nС.
Для многоступенчатого привода произвести разбивку заданного передаточного числа u по сту- пеням*, соблюдая ограничения по величине ui ( табл. 2.1) и обеспечивая равенство u=u1·u2….
Определить частоты вращения валов n0 = nЭ, ni+1= ni / ui и подсчитать крутящие моменты на валах по формуле Ti = 9550·Pi / ni , Нм.
Найденные значения использовать в последующих расчетах в качестве исходных данных.
Если техническое задание содержит кинематическую схему и параметры исполнительного органа машины, например, ленточного конвейера: скорость Vл и тяговое усилие Fл ленты, диаметр Dб приводного барабана (рис. 1.1), то, сохраняя принцип расчета, последовательно определить:
- мощности на выходном валу Pвых=10-3·Fл ·Vл и на других валах привода Pi-1= Pi / η i, используя рекомен- дуемые значения КПД η i ступеней передач (табл. 2.1);
- общее передаточное число u'=u1·u2·u3…, приняв рекомендуемые ui' его ступеней * (табл. 2.1);
- частоту вращения барабана nвых=60·10-3·Vл/(3, 14· Dб) и ожидаемую частоту двигателя n'о=nвых··u';
Выбрать типоразмер стандартного двигателя (см. приложение 1) с параметрами Pэ≥ P0 /1.05 и nэ≈ n'0 ;
Уточнить передаточные числа привода u = nэ / nвых, и его ступеней ui, обеспечив u = u1· u2· u3…;
Определить соответствующие частоты вращения валов ni=ni-1/ui и крутящие моменты на валах привода Ti = 9550·Pi /ni , Н.
Пример 2п. Энергосиловой и кинематический расчеты привода (для задания № 5.13.10.3.2).
Исходные данные**: кинематическая схема привода (рис.1); Pвых=7, 1 кВт; u=14; nс=1500 об/мин.
Цель расчета - определение параметров Pi, ni и Ti валов привода.
Составляем кинематическую схему с нумерацией i валов (рис.2.1), используемой для индексации характеристик мощностей Pi, частот вращения ni и крутящих моментов Ti на валах, а также передаточных чисел ui и КПД η i передач.
Принимаем рекомендуемые значения КПД ступеней: ременной передачи η 1=0, 95, цилиндрической передачи редуктора η 2=0, 97 и муфты η 3=0, 98 (табл. 2.1).
Определяем общий КПД привода η ПР=η 1·η 2·η 3= 0, 95·0, 97·0, 98= 0, 9 и мощности на валах Pi-1=Pi/η i: P3=Pвых=7, 1 кВт, P2=7, 1/0.98=7, 24 кВт, P1=7, 24/0, 97=7, 48 кВт, P0=7, 48/0, 95=7, 86 кВт.
Выбираем двигатель с номинальной мощностью PЭ≥ P0/1.05=7, 86/1, 05=7, 49 кВт (допуская перегрузку до 5%) и с номинальной частотой nэ≈ nс = 1500 об/мин. Принимаем двигатель 4А132S4 ГОСТ 19523-81 (см. с. 47, приложение 1): PЭ=7, 5 кВт, nЭ=1445 об/мин и dэ=38 мм - диаметр вала двигателя.
Принимаем значения передаточных чисел: редуктора u2=5 и ременной передачи u1= uПР / u2= 14 / 5= 2, 8, что соответствует рекомендуемым диапазонам передаточных чисел (табл. 2.1).
Определяем частоты вращения валов: n0= nЭ=1445 об/мин, n1=n0/u1=1445/2, 8=516 об/мин, n2=n3=n1/u2=516/5= 103 об/мин и подсчитываем крутящие моменты по формуле Ti= 9550·Pi /ni – получаем: T0=9550·Po /no=9550·7, 86/1445= 52 Нм, T1=…= 138 Нм, T2=…= 671 Нм, T3=…= 658 Нм.
Найденные значения параметров Pi, ni и Ti используем в последующих расчетах в качестве исходных данных.
* Для двухступенчатых цилиндрических редукторов обеспечить uРЕД = uБЫСТР·uТИХ ≤ 40 при uБЫСТР > uТИХ ≈ ≈ 0, 9·√ uРЕД ≈ 0, 8·uБЫСТР. Передаточные числа редукторов и их ступеней желательно задавать из стандартного ряда: … 2; 2, 5; 3, 15; 4; 5; 6, 3; 8; 10; 12, 5; 16; 20; 25; 31, 5; 40; 50; 63; 80 ….
** Здесь и в дальнейшем исходные данные приводятся в принятых обозначениях.
- 6 -
3. Расчеты зубчатых цилиндрических передач (ЗЦП)
Принцип расчета ЗЦП различных типов одинаков и отражен в методике расчета ЗЦП односту- пенчатого редуктора с последующим указанием особенностей расчета передач иных конструкций.
3.1. Расчеты передачи цилиндрического одноступенчатого редуктора
3.1.1. Проектный расчет передачи
Исходные данные: схема редуктора; Т1(2); n1(2); u; Lh; β; график нагружения: θ i, λ i.
Цель расчета – обоснование материалов и основных ожидаемых размеров передачи, удовлетво- ряющих исходным данным, критериям работоспособности и конструктивным требованиям.
Колеса зубчатых цилиндрических и конических передач изготавливают из стали обычно одной марки штампованными, добиваясь необходимых механических свойств соответствующими видами (химико-) термической обработки (Х)ТО – см. табл. 3.1 и 3.2. Колеса одноступенчатых редукторов при отсутствии жестких требований к габаритам обычно изготавливают из улучшенных сталей, обеспечивая соразмерность узлов привода и облегчая обработку зубьев, а для устранения их задира и ускорения приработки обеспечивают большую твердость зубьев шестерни НВ1 по сравнению с колесом НВ2=НВ1- (20…50). Рекомендации для многоступенчатых редукторов – см. п. 3.2.
| Таблица 3.1 | Таблица 3.2 | Таблица3.3 | |||||||||||
|
Материал колес | Вид (Х)ТО*1 |
Марка Стали |
Вид (Х)ТО *1 | Твердость *2 |
Вид (Х)ТО | σ Н O МПа | S Н | σ FO МПа | m | S F | |||
| шестерня | колесо | ||||||||||||
| Одинаков | У | У | 45 | У | 285 H B | У | 2НВ+70 | 1, 1 | 1, 75HB | 6 | 1, 7 | ||
| Одинаков | З | У | 45 | З | 48 HRC | З | 17HRC+200 | 1, 2 | 900*3 | 9 | 1.7*3 | ||
| Одинаков | З | З | 20Х | Ц | 60 HRC | Ц | 23HRC | 1, 2 | 700 | 9 | 1, 55 | ||
| Разный | Ц | З | 40ХНМА | А | 65 HRC | А | 1050 | 1, 2 | 750 | 9 | 1, 7 | ||
| Одинаков | Ц (А) | Ц (А) | *2 Средние значения твердости | *3 Для сквозной закалкиТВЧ зубьев модулем ≤ 3 мм.. При поверхностнойй закалке ТВЧ зубьев модулем > 3 мм принять: σ FO=650 МПа и SF=1, 55. | |||||||||
| *1 У - улучшение; З - закалка ТВЧ; | для заготовок сечением ≤ 80 мм. | ||||||||||||
| Ц - цементация; А - азотирование. |
| ||||||||||||
Для оценки износостойкости и прочности зубьев определить допускаемые напряжения контактной [σ ]Н1(2) и изгибной [σ ]F1(2) выносливости материала зубьев каждого из колес:
[ σ ]Н = σ HO ∙ ZN / SH и [ σ ] F = σ FO ∙ YN / SF,
где σ HO и σ FO –пределы контактной и изгибной выносливости зубьев (табл. 3.3) при числах циклов не менее базовых NHO≈ (HB*)3≤ 1, 2∙ 108 и NFO=4∙ 106 циклов.
ZN и YN – коэффициенты долговечности, зависящие от показателей степени m (табл. 3.3) кривой усталости и от соответствующих базовых и эквивалентных чисел NHE и NFE циклов нагружения:
для контактной выносливости: NHE1(2)=60∙ n1(2)∙ Lh∙ Σ (θ i3∙ λ i) ≤ NHO1(2),
и Z N1(2)= 6√ NH01(2) / NHE1(2) ≥ 1;
для изгибной выносливости: NFE 1(2)=60∙ n1(2)∙ Lh∙ Σ (θ im∙ λ i) ≤ 4∙ 106,
и YN1(2)= m√ 4∙ 106/NFE1(2) ≥ 1
(п ри твердости НВ1(2)< 350 и Z N1(2) =1 принять YN1(2)= 1).
SH и SF – коэффициенты запаса – табл. 3.3.
За расчетное допускаемое напряжение [σ ]Н цилиндрических и конических передач принять либо наименьшее из [σ ]Н1(2) = [σ ]Н MIN, либо только для непрямозубых и прирабатывающихся пере- дач при твердости колес НВ1> 350 и НВ2< 350 принять [σ ]Н = 0, 45∙ ([σ ]Н1+[σ ]Н2), но не менее [σ ]Н MIN и не более 1, 25∙ [σ ]Н MIN для цилиндрических и не более 1, 15∙ [σ ]Н MIN для конических передач.
Определить проектные характеристики ЗЦП, начиная с межосевого расстояния
a ' = Z а ∙ ( u +1)∙ 3√ T 2 ∙ К Hα ∙ KHβ ∙ KHV / ( u 2 ∙ [ σ ] H 2 ∙ ψ a ) мм,
где Т2 в Нм; [σ ]Н в МПа; Zа =450 [Н/(мм·м)]1/3- для прямозубых ЗЦП, и Zа =410 …- для косозубых;
КНα , КНβ и КHV - коэффициенты неравномерности распределения нагрузки между зубьями, по ширине зубчатого венца и коэффициент динамичности соответственно;
ψ a = b/ a - коэффициент ширины b зубчатого венца, ψ a = 2∙ ψ d/(u+1).
ψ d =b/d1 - коэффициент ширины зубчатого венца относительно делительного диаметра d1 шестерни.
Задать значение ψ a из диапазона (1…0, 5)∙ ψ a MAX, но не более 2∙ ψ d МАХ/(u+1), где значения ψ a MAX и ψ d МАХ - см. в табл. 3.4 с учетом схемы размещения колес … и твердости HB2 зубьев колеса.
Определить ψ d= ψ a∙ (u+1)/2, и установить значение КНβ , используя график Кº Нβ =f(ψ d) - рис. 3.1, и полагая: КНβ = Кº Нβ при твердости зубьев колеса HB2≤ 350, и КНβ ≈ 2, 6·Кº Нβ –1, 6 при HB2> 350.
.
* Для пересчета единиц твердости использовать: 1·HRC ≈ 10 ·HB.
| |
- 7 -
Значения КНα и КHV = 1+А∙ 10-3∙ υ t∙ (nст-2) установить, используя данные табл. 3.5, для чего подсчитать ожидаемую окружную скорость в зацеплении υ t ´ = (1, 1…0, 6)∙ 10-3∙ n1∙ 3√ T1/u м/с (большее значение при твердости HB1(2)≤ 350) и выбрать степень точности nст передачи – табл. 3.6.
Полученное значение a ' округлить либо до стандартного значения а (…80; 100; 125; 140; 160; 180 ….мм), либо числом кратным 5, и определить ширину зубчатого венца b = ψ a∙ а.
| Таблица3.4 | Таблица3.5 | Таблица3.6 | ||||||||||||
|
НВ | Значения коэффициентов Ψ * а МАХ и ( Ψ d МАХ ) для схемы расположения колес по рис. 3.1 | β | К H α =К F α | А | nC Т не грубее | vt м/c не более | ||||||||
| β =0 | β > 0 | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | a** | б** | 6 | 20 | 30 | |||||
| a** | 0, 25 (0, 7) | 0, 3 (1, 3) | 0, 35 (1, 4) | 0, 4 (1, 5) | 0, 5 (1, 6) | β =0 | 1+0, 06·(nC-5) | 8 | 5 | 7 | 12 | 20 | ||
| б** | 0, 2 (0, 3) | 0, 25 (0, 7) | 0, 3 (0, 8) | 0, 35 (0, 9) | 0, 4 (1, 0) | β > 0 | 1+0, 15· (nC-5) | 3 | 2 | 8 | 6 | 10 | ||
| * Ψ а МИН = 0, 15. ** a – при твердости колеса НВ2 ≤ 350 НВ, б – при твердости колеса НВ2 > 350 НВ. | 9*** | 2 | 4 | |||||||||||
| *** для открытых передач | ||||||||||||||
 Принять модуль зацепления из диапазона m=(0, 015±0, 005)· a, округлив его до стандартного значения: 1; 1.25; 1, 5; 1, 75; 2; 2, 5; 3; 4; 5 … мм.
Принять модуль зацепления из диапазона m=(0, 015±0, 005)· a, округлив его до стандартного значения: 1; 1.25; 1, 5; 1, 75; 2; 2, 5; 3; 4; 5 … мм.
Определить: - числа z1(2) зубьев колес, приняв для косозубой передачи ожидаемый угол β ' наклона зубьев из диапазона β =(14±6)о,
(z1+z2)≈ 2·a·cos β ' / m, z1 ≈ (z1+z2)/(u+1) ≥ 17 ·cos3 β ', z 2= (z1+z2) - z1;
- передаточное число u ф =z2/z1 (допустимо отличие от заданного u до 2, 5%);
- угол наклона зубьев фактический β =Arc cos [(z1+z2)·m/(2∙ а)] ≤ 20 о;
- диаметры колес делительные d 1 =2· a /(z2/z1+1) и d 2 =d1·z2/z1 [d1+ d2=2· aw]
и диаметры вершин da1(2)=d1(2) + 2·m и впадин df1(2)=d1(2) – 2, 4·m зубьев;
- окружную скорость υ t=π ·d1∙ n1/(60∙ 103) м/с, по которой возможно уточнение
степени точности nст передачи и коэффициентов КНα и КHV;
Рис. 3.1 - силы в зацеплении: окружную Ft =2·103·Т1/d1, радиальную Fr =Ft∙ tg 20º /cos β и
осевую Fa = Ft∙ tg β в Н.
3.1.2. Проверочный расчет передачи на контактную выносливость
Исходные данные: Ft; d2; b; uф; β; z1; z2; КНα ; КНβ ; КHV; [σ ]H.
Цель расчета – проверка материала и размеров ЗЦП из условия контактной выносливости (износостойкости) зубьев колес: [ σ ] H ≥ σ H = 483∙ Z ε ∙ cos β · √ Ft ∙ KHα ∙ KHβ · KHV ∙ ( u ф +1)/( d 2 ∙ b ) МПа,
где Zε – коэффициент длины контактных линий, зависящий от коэффициента ε α торцевого перекрытия ε α =[1, 88–3, 2·(1/z1+1/z2)] cos β, для прямозубых ЗЦП – Zε =√ (4- ε α )/3; для косозубых – Zε =√ 1/ ε α .
Сделать вывод о контактной выносливости ЗЦП, допуская перегрузку до 5% и недогрузку до 20%; иначе – изменить ЗЦП: либо заменить материал или твердость колес, либо – их степень точности, либо – размеры ЗЦП [приняв a ≈ a∙ ([σ ]H/σ H) 2/3]; при этом соответствующие расчеты повторить.
3.1.3. Проверочный расчет передачи на изгибную выносливость
Исходные данные: Ft; b; m; z1(2); β; ε α ; [σ ]F1(2).
Цель расчета – проверка материала и размеров ЗЦП из условия изгибной выносливости (прочности) зубьев колес: [ σ ] F 1(2) ≥ σ F 1(2) = Ft ∙ К F α ∙ К F β ∙ К FV ∙ YF 1(2) ∙ Yβ ∙ Y ε /( b ∙ m ) МПа,
|
Таблица 3.7 | |||||
|
Твердость колеса | К F β | К FV | Y ε | ||
| β = 0 | β > 0 | ||||
| HB2 ≤ 350 | 2, 2КНβ –1, 2 | 2КНV–1 | 1/КF α | 1/ε α | |
| HB2 > 350 | 1, 6КНβ – 0, 6 | КНV | |||
где YF – коэффициент формы зуба, зависящий от эквивалентного числа z V зубьев и коэффициента x смещения: при zV1(2)=z1(2)/cos3 β найти YF 1(2) =3, 5+10, 7/ zV 1(2) –23, 6·x1(2)/zV1(2)–0, 18·x21(2) (при отсутствии смещения x1=x2=0);
Yβ – коэффициент угла наклона зубьев, Yβ =1– β º /140º;
Yε – коэффициент длины контактных линий – см. табл. 3.7;
КFα , КFβ и КFV – коэффициенты неравномерности нагрузки. Принять КFα =КНα , а значения КFβ и КFV – см. табл. 3.7.
Сделать вывод об изгибной выносливости зубьев колес, допуская их перегрузку до 5%, иначе – изменить ЗЦП: либо заменить материал или (X)ТО зубьев, либо степень точности передачи, либо ввести смещения зубьев на 2·m·x1(2) (принять коэффициенты смещения у шестерни 0 < x 1 ≤ 0, 5 и у колеса x 2 = – x1, при этом изменятся диаметры вершин da1(2) = d1(2) + 2·m + x1(2)·m и впадин df1(2) = d1(2) – 2, 4·m + 2·m·x1(2) зубьев и коэффициенты YF 1(2)), либо изменить размеры ЗЦП (принять m ≥ m∙ [σ ]F/σ F и а w ≈ 9∙ m ∙ (u+1)/cos β '); при этом соответствующие расчеты повторить.
Выполнить эскиз ЗЦП, с указанием принятых размеров, например, см. рис. 3.2.
- 8 –
3.2 Особенности расчетов ЗЦП иных конструктивных типов
ЗЦП многоступенчатых редукторов проектировать с учетом унификации материала и зубо- резного инструмента. Для минимизации габаритов редуктора целесообразно материал передач зада- вать с повышенной износостойкостью - твердость зубьев особенно шестерен д.б. НВ1> 350 (у быстроходной ступени м.б. целесообразным НВ1(2)< 350 ), и все передачи проектировать косозу- быми. Передаточные числа ступеней целесообразно назначать с учетом ограничений (табл. 2.1) и в последовательности возрастания от тихоходной ступени к быстроходной, с коэффициентом геометрической прогрессии ≈ 1, 2. Расчеты каждой ступени выполнять по изложенной выше (п. 3.1) методике, начиная их с тихоходной ступени, как более нагруженной и габаритной, стремясь обеспечить минимально приемлемое межосевое расстояние при большей ширине колес каждой ступени.
Для редукторов с расположением осей колес в горизонтальной плоскости стремятся создать рациональное погружение колес (а не шестерен) в масляную ванну, обеспечивая соотношение делительных диаметров колес быстроходных ступеней (Б) к тихоходной (Т) d2 Бi ≈ (0, 7…1, 0)·d2 Т, при этом межосевые расстояния быстроходных ступеней a Бi*≈ (0, 35…0, 5)·d2 Т ·( u Бi+1)/u Бi.
Для соосных редукторов (см. с.4, задания по схеме 8) обеспечить равенство межосевых
расстояний ступеней передач a Б = a Т.
Открытые ЗЦП проектировать прямозубыми, обеспечивая окружные скорости vt ≤ 2 м/с, поскольку они работают в условиях интенсивного абразивного износа и скудной смазки и являются прирабатывающимися при любой твердости зубьев. Их расчеты выполнять по изложенной (п. 3.1) выше методике с учетом того, что допускаемые напряжения контактной и изгибной выносливости определять по пределам длительной выносливости [σ ]Н = σ HО/SH и [σ ]F = σ FО/SF (т.е. при Z N =
YN = 1), а модуль зацепления задавать в 1, 5…2 раза больше чем у закрытых ЗЦП (что учитывает износ зубьев при допустимом утонении их вершин до 0, 25·m).
Пример 3п. Расчеты косозубой цилиндрической передачи одноступенчатого редуктора
3.1п. Проектный расчет передачи
Исходные данные: Т1(2)=138 (671) Нм; n1(2)=516 (103) об/мин; u=5; Lh=10000 час;
график нагружения двухступенчатый: θ 1(2)=1 (0, 8), λ 1(2)=0, 1 (0, 9).
Цель расчета - обоснование ожидаемых размеров ЗЦП, удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям.
Принимаем материал колес одинаковым - сталь 45, ТО (табл. 3.2) - улучшение до твердости шестерни НВ1=285 и колеса- НВ2 =НВ1-(20…50)≈ 285-25 =260.
Определяем допускаемые напряжения материала колес для контактной [σ ]H1(2) = σ HО1(2)·ZN1(2)/SH1(2) и изгибной выносливости [σ ]F1(2) = σ FO1(2)·YN1(2)/SF1(2),
где σ HО2 и σ FO1(2)- соответствующие пределы длительной выносливости зубьев при числах циклов нагружения не менее базовых NHО(FО): σ HО2=2·НВ2+70 МПа при NHО2≈ НВ23 и σ FO1(2) =1, 75·НВ1(2) МПа при NFО1(2)=4·106;
ZN и YN – коэффициенты долговечности, зависящие от эквивалентных чисел NHE (FЕ) циклов нагружения:
ZN2= 6√ NH02 / NHE2 ≥ 1 при NHE2=60∙ n2∙ Lh∙ Σ (θ i3·λ i) и YN1(2)= 6√ 4∙ 106/ NFE1(2) ≥ 1 при NFE 1(2)=60∙ n1(2)∙ Lh∙ Σ (θ i6·λ i);
SH и SF – коэффициенты запаса, для принятого материала колес SH1(2)=1, 1 и SF1(2) =1, 7 (табл. 3.3).
При этом допускаемое напряжение контактной выносливости передачи определяем по колесу (т. к. НВ1(2)< 350): для NHE2=60∙ 103·10000·(13·0, 1+0, 83·0, 9)=3, 47·107, что больше, чем NHО2=2603=1, 75·107, по этому примем ZN2=1, и, следовательно, [σ ] Н =[σ ]Н2=(2·260+70)·1/1, 1= 536 МПа.
Допускаемые напряжения изгибной выносливости зубьев находим, приняв YN1(2)=ZN2=1,
[σ ] F 1 =1, 75·285·1/1, 7= 293 МПа и [σ ] F 2 =1, 75·260·1/1, 7= 268 МПа.
Определяем ожидаемое межосевое расстояние передачи из условия износостойкости (контактной выносливости) передачи a' =410·(u+1)∙ 3√ T2∙ КHα ∙ KHβ ∙ KHV / (u2∙ [σ ]H2∙ ψ a) мм,
где КНα , КНβ и КHV- коэффициенты неравномерности распределения нагрузки между зубьями, по ширине зубчатого венца и коэффициент динамичности;
ψ a – коэффициент ширины b зубчатого венца.
Принимаем ψ a MAX =0, 5 и ψ d МАХ=1, 6 (табл. 3.4 для схемы 5 и НВ2< 350 HB) и задаем ψ a=0, 4, что соответствует диапазону ψ a = (1…0, 5)∙ ψ a MAX = (1…0, 5)∙ 0, 5=0, 5…0, 25, и не превышает 2∙ ψ d МАХ/(u+1)= 2∙ 1, 6/(5+1) = 0, 53.
Определяем коэффициент ψ d = ψ a∙ (u+1)/2=0, 4∙ (5+1)/2=1, 2. При этом находим (рис. 3.1) коэффициент неравномерности нагрузки KHβ = Кº Нβ = 1, 06.
.
* В дальнейшем проконтролировать зазор не менее 2 мм между тихоходным колесом и быстроходным валом.
- 9 -
.
Определим ожидаемую скорость в зацеплении vt ´ ≈ 1, 1∙ 10-3∙ n1∙ 3√ T1/u=1, 1∙ 10-3∙ 516·3√ 138/5= 1, 7м/с, по которой задаем степень точности передачи n 'ст= 8 (табл. 3.6), и находим коэффициенты неравномерности:
КНα =1+0, 15·(nст-5)=1+0, 15·(8-5)= 1, 45 и К HV =1+3∙ 10-3∙ vt ∙ ( n ст -2)=1+3∙ 10-3∙ 1, 7∙ (8-2)= 1, 03 (табл. 3.5).
При этом a ' =410·(5+1)∙ 3√ 671·1, 45·1, 06·1, 03/(52·5362·0, 4) ≈ 177 мм.
Принимаем стандартное значение a = 180 мм, тогда b =ψ a∙ a =0, 4·180= 72 мм.
Определяем:
- модуль зацепления, удовлетворяющий диапазону m=(0, 015±0, 005)· a =(0, 01…0, 02)·180=1, 8…3, 6 мм, принимаем стандартный модуль m =2, 75 мм;
- числа зубьев колес, приняв ожидаемый угол наклона зубьев косозубой передачи β '=12о:
(z1+z2)=2·a·cos β ´ / m=2·180·cos 12о / 2, 75≈ 128,
z1 =(z1+z2)/(u+1)=128/(5+1)≈ 21 > 17·cos3 β =17·cos3 12о≈ 16, z2= 128-21= 107;
- фактическое передаточное число uф=z2/z1=107/21= 4, 952 (погрешность Δ u=1 % ≤ [2, 5%]);
- угол наклона зубьев β =Arccos [(z1+z2)·m/(2∙ a)] = Arccos [128·2, 75/(2·180)] = 12о6'6'' ≈ 12, 1о.
- делительные диаметры колес d 1 =2· a/(z2/z1+1)=2·180/(107/21+1)= 59, 063 мм и
d 2 =d1·z2/z1=59, 063·107/21= 300, 937 мм;
- диаметры вершин da1(2)=d1(2) + 2·m и впадин df1(2)=d1(2) – 2, 4·m зубьев колес
da1 = 59, 063+2·2, 75 ≈ 64, 56 мм, df1 = 59, 063-2, 5·2, 75 ≈ 52, 19 мм,
da2 = 300, 937+2·2, 75 ≈ 306, 44 мм, df2 = 300, 937-2, 5·2, 75 ≈ 294, 06 мм;
- окружную скорость vt =π ·d1∙ n1/(60∙ 103)=π ·59, 063·516/60000≈ 1, 6 м/с, что практически совпадает с ожидаемой
скоростью vt´ и, значит, степень точности передачи и значения коэффициентов КНα и КHV сохраняются;
- силы в зацеплении: окружную Ft =2·103·Т1/d1=2·103 ·138 /59, 063= 4673 Н,
радиальную Fr=Ft∙ tg 20º /cos β = 4673∙ tg 20º /cos 12, 1о ≈ 1740 Н и осевую Fa= Ft·tg β =4673∙ tg 12, 1 о≈ 1000 Н.
3.2п. Проверочный расчет передачи на контактную выносливость
Исходные данные: Ft=4673 Н; d2≈ 300, 9 мм; b =72 мм; uф =4, 95; β ≈ 12, 1 о;
z1=21; z2=107; КНα =1, 45; КНβ =1, 06; КHV=1, 03; [σ ]H=536 МПа.
Цель расчета – проверка материала и размеров передачи из условия контактной выносливости (износо- стойкости) зубьев колес: [σ ]H ≥ σ H = 483∙ Zε ∙ cos β ·√ Ft∙ KHα ∙ KHβ ·KHV∙ (uф +1)/(d2∙ b) МПа,
где Zε – коэффициент длины контактных линий, зависящий от коэффициента ε α перекрытия, .
при ε α =[1, 88–3, 2·(1/z1+1/z2)]·cos β =[1, 88–3, 2·(1/21+1/107)]· cos 12, 1о =1, 66 получаем Zε =√ 1/ε α =√ 1/1, 66= 0, 78.
При этом σ H = 483∙ 0, 78∙ cos 12, 1 о·√ 4673∙ 1, 45∙ 1, 06∙ 1, 03∙ (4, 95+1)/(300, 9∙ 72)= 527 МПа, что на 2% меньше, чем [σ ]H=536 МПа, следовательно, износостойкость (контактная выносливость) передачи обеспечена.
3.3п. Проверочный расчет передачи на изгибную выносливость
Исходные данные: Ft=4673 Н; b =72 мм; m=2, 75 мм; z1=21; z2=107;
β ≈ 12, 1 о; ε α =1, 66; [σ ]F1=293 МПа; [σ ]F1(2)=268 МПа.
Цель расчета - проверка материала и размеров передачи из условия изгибной выносливости (прочности) зубьев шестерни и колеса: [σ ]F1(2) ≥ σ F1(2) = Ft∙ КFα ∙ КFβ ∙ КFV∙ YF1(2)∙ Yβ ∙ Yε /(b∙ m) МПа,
где YF – коэффициент формы зуба, зависящий от эквивалентного числа zV зубьев и коэффициентов
х1(2) смещения; при zV1(2)=z1(2)/cos3 β и при отсутствии смещения х1(2)=0 получаем:
для шестерни zV1= 21/ cos3 12, 1 о ≈ 22 и YF1=3, 5+10, 7/zV1=3, 5+10, 7/22= 4, 0,
для колеса zV2 =107/ cos3 12, 1 о≈ 114 и YF2=3, 5+10, 7/zV2=3, 5+10, 7/114= 3, 6;
Yβ – коэффициент угла наклона зубьев, Yβ =1–β º /140º =1-12, 1/140= 0, 91;
Yε – коэффициент длины контактных линий, Yε =1/ε α =1/1, 66= 0, 6;
КFα , КFβ и КFV - коэффициенты неравномерности распределения нагрузки.
Принимаем КFα =КНα = 1, 45; КFβ =2, 2·КHβ -1, 2=2, 2·1, 06-1, 2= 1, 13; КFV=2·КHV-1=2·1, 03-1= 1, 06 (табл.3.7).
При этом σ F 1 =4673∙ 1, 45∙ 1, 13∙ 1, 06∙ 4, 0∙ 0, 91∙ 0, 6/(72∙ 2, 75)= 89, 5 МПа < [σ ]F1= 293 МПа, и
σ F 2 =σ F1∙ YF2/YF1=89, 5·3, 6/4= 82 МПа < [σ ]F2= 268 МПа, следовательно, изгибная выносливость передачи установленных размеров (рис.3.2) обеспечена.
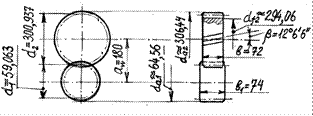
Рис. 3.2
- 10 -
4. Расчеты прямозубой конической передачи (ЗКП)
4.1. Проектный расчет передачи
Исходные данные: Т1(2); n1(2); u; Lh; график нагружения: θ i, λ i.
Цель расчета – обоснование материалов и основных размеров ортогональной ЗКП редуктора, удов- летворяющих исходным данным, критериям работоспособности и конструктивным требованиям.
Выбрать материал колес и определить показатели их контактной [ σ ]Н и изгибной [ σ ] F 1(2) выносливости согласно п. 3.1, т.к. принцип, условия работы и критерии расчета зубчатых передач конических и цилиндрических одинаковы.
Принять коэффициент K′ be=b/Re ширины b зубчатого венца относительно Re- внешнего конусного рас- стояния K ′ be ≤ 1, 17/ u, но не более 0, 3, что учитывает особенности изготовления и неподрезание зубьев.
Определить ожидаемый внешний делительный диаметр шестерни
d ' e 1 ≈ 970·3√ T 1 ∙ KHβ ∙ KHV /[ u ·[ σ ] H 2 · Kbe ·(1- Kbe /2)2] мм,
где Т1 в Нм ; [σ ]Н в МПа; КНβ и КHV - коэффициенты распределения нагрузки по ширине зубчатого венца и динамичности.
Для этого установить: - значение КНβ , используя график Кº Нβ =f(ψ d) - см. рис. 3.1 для схемы 1 (консоль- ное размещение шестерни относительно опор вала) при величине коэффициента ψ d = 0, 166·√ u2+1;
- и значение КHV, приняв скорость в зацеплении υ 't≈ 0, 8∙ 10-3∙ n1∙ 3√ T1/(u∙ Kbe) м/с и соответствующую сте-
пень точности n'ст передачи (при υ t ≤ υ MAX =5 м/с принять nст ≤ 7, при υ t ≤ υ ПРЕДЕЛЬНОЕ =8 м/с - nст≤ 6).
При этом принять КHV=1+8∙ 10-3∙ υ t∙ (nст-1) для HB2≤ 350 или К HV= 1+5∙ 10-3∙ υ t∙ (nст -1) для HB2> 350.
Определить: - внешний модуль зубьев me * ≈ K′ be·de1·√ u2+1/20, округлив его до ближайшего значения с точностью до 0, 1 мм;
- числа зубьев колес z 1 ≈ de1/me и z 2 ≈ u∙ z1;
- передаточное число фактическое u ф = z2/z1 (допускается отклонение от заданного u до 2, 5%);
- внешние делительные диаметры колес de1(2) = z1(2)·me;
- углы делительных конусов õ 2 = Аrc tg uФ и õ 1 = 90o- õ 2;
- внешнее конусное расстояние Re=√ de12+de22 и ширину венца b≤ 10∙ me, обеспечив Kbe=b/Re≤ K′ be;
- средний делительный диаметр шестерни dm 1 =de1∙ (Re-b/2)/Re и средний модуль mm = dm1/z1;
- скорость в зацеплении υ t= π ·dm1∙ n1/(60∙ 103) м/с (при отличии ∆ υ t=(1-υ ′ t/υ t)∙ 100> 5% уточнить степень nст точности передачи и коэффициент КHV - см. выше);
- силы в зацеплении: окружную для шестерни и колеса Ft = 2·103 ·Т1/dm1,
радиальную для шестерни и осевую для колеса Fr 1 = Fa 2 = Ft∙ tg 20º ·cos õ 1,
осевую для шестерни и радиальную для колеса Fa 1 = Fr 2= Ft∙ tg 20о·cos õ 2 в Н.
4.2. Проверочный расчет передачи на контактную выносливость
Исходные данные: Ft; dm1; b; n1; õ 1; КНβ ; К'HV; υ t'; n'ст; [σ ]H.
Цель расчета – проверка материала и размеров передачи из условия контактной выносливости (износостойкости) зубьев: [ σ ] H ≥ σ H = 470· √ Ft ∙ KHβ · KHV / ( dm 1 ∙ b ∙ cos õ 1 ) МПа,
здесь использовать уточненное значение коэффициента динамичности KHV, если скорость в зацеплении υ t ≠ υ t', что влечет изменение степени точности nст передачи - см. выше.
Сделать вывод о контактной выносливости ЗКП, допуская ее перегрузку до 5% и недогрузку до 20%; иначе – внести изменения в конструкции ЗКП: заменить либо материал или твердость колес, либо размеры передачи, приняв иное значение коэффициента Kbe, либо ее степень точности; при этом соответствующие расчеты повторить.
4.3. Проверочный расчет передачи на изгибную выносливость
Исходные данные: Ft; b; mm; z1(2); õ 1(2); КHβ ; КHV; [σ ]F1(2).
Цель расчета – проверка материала и размеров передачи из условия изгибной выносливости (прочности) зубьев шестерни и колеса: [ σ ] F 1(2) ≥ σ F 1(2) = Ft ∙ К F β ∙ К FV ∙ YF 1(2) / (0, 85· b ∙ mm ) МПа,
где КFβ - коэффициент неравномерности нагрузки по длине зуба, КFβ =0, 18+0, 82∙ KHβ ;
КFV - коэффициент динамичности, КFV ≈ 1, 5·КHV - 0, 5;
YF1(2) - коэффициенты формы зуба, зависящие от эквивалентных чисел zV1(2) зубьев и коэффи- циентов смещений x1(2) (при отсутствии смещений x1=x2=0):
z V1(2) = z1(2) /cos õ 1(2), Y F1(2) = 3, 5+10, 7/ zV 1(2) –23, 6·x1(2)/zV1(2)–0, 18·x21(2) ;
Сделать вывод об изгибной выносливости зубьев, допуская перегрузку до 5%, иначе – изменить ЗКП: либо заменить материал или твердость зубьев колес, либо степень точности передачи, либо ввести смещение зубьев на 2·m·x1(2) ( принять рекомендуемые коэффициенты смещения у шестерни x 1 = (2-2/uФ)/√ z1 и у колеса x 2 = – x1), либо изменить размеры передачи, приняв иное значение коэффициента Kbe,; и необходимые расчеты повторить.
Выполнить эскиз ЗКП, с указанием принятых размеров.
* Возможно уменьшение me при Kbe=20·me·√ u2+1/d′ e1 и конструктивной приемлемости полученных значений de1 и b.
- 11 -
Пример 4п. Расчеты прямозубой конической передачи одноступенчатого редуктора
4.1п. Проектный расчет передачи
Исходные данные: Т1=50 Нм; n1(2)=1425(452) об/мин; u=3, 15; Lh; =10000 час;
График нагружения двухступенчатый: θ 1(2)=1 (0, 8), λ 1(2)=0, 1 (0, 9).
Цель расчета – обоснование материала и ожидаемых размеров передачи, удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям.
Т.к. методика выбора материала и определения допускаемых напряжений контактной [σ ]Н и изгибной [σ ]F1(2) выносливости для конических и цилиндрических зубчатых передач одинаковы (см. п. 4.1), а исходные данные проектируемой передачи близки к таковым в примере 3п, то примем материал конических колес такой же как в примере 3п: сталь 45 при твердости НВ1(2)=285(260), и сохраним значения допускаемых напряжений [σ ] H = 536 МПа, [σ ] F 1 = 293 МПа и [σ ] F 2 = 268 МПа (расчеты [σ ]H(F) выполнить аналогично расчету в примере 3п).
Принимаем коэффициент K′ be=b/Re ширины b зубчатого венца относительно Re - внешнего конусного расстояния K′ be≤ 1, 17/ u = 1, 17/ 3, 15 = 0, 371, но не более 0, 3, поэтому принято K ′ be =0, 3;
Определяем ожидаемый внешний делительный диаметр шестерни
d ' e 1 ≈ 970·3√ T1∙ KHβ ∙ KHV/[u·[σ ]H2·Kbe·(1-Kbe/2)2] мм,
где КНβ и КHV - коэффициенты распределения нагрузки по ширине зубчатого венца и динамичности.
Для этого находим коэффициент КНβ, используя график К º Нβ =f(ψ d)- см. рис. 2.1 для схемы 1 – консольного размещения шестерни относительно опор вала и при величине коэффициента ψ 'd=0, 166·√ u2+1= =0, 166·√ 3, 152+1 = 0, 55: принимаем КНβ = К º Нβ = 1, 15. Определяем ожидаемую скорость в зацеплении v't ≈ ≈ 0, 8∙ 10-3∙ n1∙ 3√ T1/(u∙ Kbe)= 0, 8∙ 10-3∙ 1430∙ 3√ 50/(3, 15∙ 0, 3)= 4, 4 м/с, по которой устанавливаем степень точности передачи n'ст=7, и коэффициент К' HV = 1+8∙ 10-3∙ vt ∙ ( n ст -1) =1+8∙ 10-3∙ 4, 5∙ (7-1)=1, 21.
При этом d ′ e 1 =970·3√ 50∙ 1, 15∙ 1, 21/[3, 15·5362·0, 3·(1-0, 3/2)2] ≈ 68, 7 мм. .
Определяем: - внешний модуль зубьев me ≈ Kbe·d′ e1·√ u2+1 / 20=0, 3·68, 7·√ 3, 152+1 / 20≈ 3, 4 мм;
- числа зубьев колес z 1 ≈ d′ e1/ me=68, 7/3, 4≈ 20 и z 2 ≈ z1∙ u=20·3, 15= 63;
- внешние делительные диаметры колес de 1 = z1·me=20·3, 4= 68, 00 мм и de 2 = z2·me=63·3, 4= 214, 20 мм;
- углы делительных конусов õ 2 = Аrc tg u Ф = А rc tg 3, 15=72о23’’15’= 17, 4 о и õ 1 = 90o- õ 2=…= 72, 6 о;
- внешнее конусное расстояние Re=√ de12+de22=√ 682+214, 22= 112, 37 мм и ширину венца b =33 мм, что менее чем
bМАХ=10∙ me=34 мм, и при этом соблюдено условие Kbe=b/Re=33/112, 37=0, 294 < K′ be=0, 3;
- средний делительный диаметр шестерни dm 1 =de1∙ (Re-b/2)/Re=68∙ (112, 37-33/2)/112, 37= 58, 02 мм и средний
модуль mm = dm1/z1; =58, 02/20= 2, 9 мм;
- скорость в зацеплении υ t= π ·dm1∙ n1/(60∙ 103)= π ·58, 02∙ 1425/(60∙ 103)≈ 4, 3 м/с, при этом отличие ∆ υ t=(1-υ ′ t/ υ t)∙ 100=
=(1-4, 4/4, 3)∙ 100 ≈ -2% < [±5%], и значит сохраняется степень nст точности передачи и коэффициент К'HV;
- силы в зацеплении: окружную для шестерни и колеса Ft =2·103·Т1/dm1, = 2·103·50/58, 02= 1724 Н,
радиальную для шестерни и осевую для колеса Fr1=Fa2=Ft∙ tg 20º · cos õ 1 = 1724∙ tg 20º · cos 17, 4о= 600 Н и
осевую для шестерни и радиальную для колеса Fa1 = Fr2 =Ft∙ tg 20о· cos õ 2=1724∙ tg 20о· cos 72, 6о = 190 Н.
4.2п. Проверочный расчет передачи на контактную выносливость
Исходные данные: Ft=1724 Н; dm1=58, 02 мм; b=33 мм; õ 1≈ 17, 4о; n1=1425 об/мин;
КНβ =1, 25; К'HV=1, 21; vt=4, 3 м/с; n'ст=7; [σ ]H=536 МПа.
Цель расчета – проверка материала и размеров передачи из условия контактной выносливости (износо- стойкости) зубьев колес: [σ ]H ≥ σ H = 470·√ Ft ∙ KHβ · KHV / ( dm 1∙ b ∙ cos õ 1 ) = .
= 470·√ 1724∙ 1, 15·1, 21 /(58, 02∙ 33∙ cos 17, 7о)= 539 МПа, что на 0, 6% превышает [σ ]H=536 МПа при допустимой перегрузке 5%, т.е. контактная выносливость передачи достаточна.
4.3п. Проверочный расчет передачи на изгибную выносливость
Исходные данные: Ft=1724 Н; b=33 мм; mm=2, 9 мм; õ 1(2)≈ 17, 4о (72, 6о);
z1(2)=20(63); КНβ =1, 15; КHV=1, 21; [σ ]F1(2)=293 (268) МПа.
Цель расчета – проверка материала и размеров передачи из условия изгибной выносливости (прочности) зубьев колес: [σ ]F1(2) ≥ σ F1(2) = Ft∙ КFβ ∙ КFV∙ YF1(2) / (0, 85·b∙ mm) МПа,
где КFβ и КFV – коэффициенты концентрации нагрузки по длине зуба и динамичности,
принимаем КFβ =0, 18+0, 82·КНβ =0, 18+0, 82·1, 15= 1, 12 и КFV=1, 5·КHV -0, 5=1, 5·1.21-0, 5= 1, 33;
YF- коэффициент формы зуба, зависящий от эквивалентного числа zV зубьев (смещение х1=х2=0),
для шестерни zV1 = z1/cos õ 1 = 20/cos 17, 4о = 21 и YF1 = 3, 5+10, 7/zV1=3, 5+10, 7/21 = 4, 01,
для колеса zV2= z2/cos õ 2 =63 /cos 72, 6о = 208 и YF2= 3, 5+10, 7/208= 3, 56.
При этом σ F 1 = 1724∙ 1, 12∙ 1, 33∙ 4, 01 / (0, 85·33·2, 9) = 127 МПа < [σ ]F1 = 293 МПа и
σ F 2 = σ F1·YF2/YF1 = 127·3, 56/4, 01 = 113 МПа < [σ ]F2 = 268 МПа, т.е. прочность зубьев колес также обеспечена.
- 12 -
5. Расчеты червячной передачи (ЧП)
Ниже приведена методика расчета ЧП редукторов с цилиндрическими червяками и распространенными профилями витков: эвольвентным (Z1), архимедовым (ZA) и конволютным (ZK).
5.1. Проектный расчет передачи
Исходные данные: Т2; u; n1(2); P2; Lh; график нагружения: θ i, λ i.
Цель расчета – обоснование материалов и основных размеров ЧП редуктора, удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям.
ЧП изготавливают из материалов, образующих антифрикционную пару, что повышает их КПД путем снижения потерь на трение скольжения в червячном зацеплении. Червяки изготавливают из сталей, обычно, с поверхностной закалкой, шлифовкой и полировкой витков, что повышает нагру- зочную способность ЧП. Зубчатые венцы червячных колес изготавливают из оловянистых бронз (группа 1; табл.5.1), работающих при скоростях скольжения в зацеплении vS£ 25…35 м/с; или безоловянистых бронз и латуней (группа 2) при vS £ 4…5 м/с (применение серых чугунов ограничено единичным производством в основном для ЧП с ручным приводом). .
Принять материал колеса с учетом ожидаемой скорости скольжения vS' ≈ 0, 45∙ 10-3∙ n1∙ 3√ T2 м/с (здесь T2 в Нм; n1 в об/мин), но не больше допустимой [v]S ≥ vS (табл. 3.1). В дальнейшем по итогам расчета при [v]S ≥ vS уточнить материал колеса.
Для обоснования размеров ЧП определить допускаемые напряжения контактной [s]H и изгибной [s]F выносливости материала зубьев колеса по формулам, приведенным в табл. 3.1, где обозначено: [s]Fо –исходное допускаемое напряжение изгиба; NHE и NFE – эквивалентные числа циклов нагружения зубьев.
Таблица 5.1
|
Материал | Вид литья* | s в / s т, МПа |
Допускаемые напряжения, МПа | ||
| - | Марка | ||||
| Группа 1 | БрО10Н1Ф1 [ v ] S £ 25 м/с | Ц | 285/165 | . [s]н** = 0, 9∙ sв∙ 8√ 107/NHE, где NHE = 60∙ n2∙ Lh∙ S(qi4∙ li); при 1, 5∙ 105 ≤ NHE ≤ 25∙ 107. |
. [s]F=[s]F0∙ 9√ 106/NFE, где [s]F0=0, 25·sт + 0, 08·sв; NFE =60∙ n2∙ Lh∙ S(qi9∙ li); при 106 ≤ NFE ≤ 25∙ 107.
|
| БрО10Ф1 [ v ] S £ 12 м/с | К | 245/195 | |||
| Группа 2 |
БрА10Ж4Н4 [ v ] S £ 5 м/с | Ц | 700/460 |
[s]н** = 300 – 25∙ vS, здесь vS в м/с. | |
| К | 650/430 | ||||
|
ЛАЖ M ц66-6-3-2 [ v ] S £ 4 м/с | Ц | 500/330 | |||
| К | 450/295 | ||||
* Виды литья: Ц - центробежное; К - в кокиль (при единичном производстве применяют литье в песок).
** Для неполированных витков червяка твердостью < 45 HRC, или при расположении червяка вне масляной ванны значения [ s ]Н снизить на 15…20%.
Определить проектные характеристики ЧП, начиная с межосевого расстояния
aw / ≈ 610 ∙ 3√ T 2 · k н / [ σ ] H 2 мм,
где Т2 в Нм; [s]H в МПа; kн ≈ 1, 1±0, 1 – коэффициент нагрузки.
Полученное значение aw / округлить до кратного 10 или 5 или до стандартного а w (...63; 80; 100; 125; 140; 160; 180, ... мм).
Принять число z 1 заходов червяка: z1=4 при u < 15, z1=2 при 15 ≤ u ≤ 30 (40*), z1=1 при u > 30;
Определить диапазон приемлемых чисел зубьев колеса z2MIN ≥ 0, 96·u·z1 и z2MAX ≤ 1, 04·u·z1, ограниченный допустимой погрешностью передаточного числа ±4%;
Принять:
- коэффициент диаметра червяка наименьшим стандартным значением из условия q ≥ 0, 2× z2MIN,
- модуль зацепления наибольшим стандартным значением из диапазона m ≤ 2·а w / (z2MIN + q ±2);
при этом обеспечить необходимое сочетание** стандартных значений m и q – см. табл. 5.2.
Таблица 5.2
| m, мм | 2; 2, 5; 3, 15; 4; 5 | 6, 3; 8; 10; 12, 5 | 16 |
| q | 8; 10; 12, 5; 16; 20 | 8; 10; 12, 5; 14; 16; 20 | 8; 10; 12, 5; 16 |
- число зубьев колеса ближайшим к z2 ≈ u× z1 целым числом из установленного диапазона, до-
полненного геометрическими ограничениями z2 = 2· а w / m – q ± 2.
Определить коэффициент смещения червяка x = а w / m – (z2 + q) / 2 и проверить принятые значения а w, m, q и z2 по условию +1 ³ x ³ -1.
.
* Рекомендация: “z1=2 при 15≤ u ≤ 40 ” соответствует предельному значению z2MAX=80 для редукторов.
** При отсутствии приемлемых сочетаний m и q принять иное значение а w , и повторить подбор.
- 13 -
Определить:
- делительные диаметры d1(2) витков червяка (зубьев колеса), диаметры da1(2) их выступов
и df1(2) – впадин: d1 = m× q; d21 = d1 + 2× m; df1 = d1 - 2, 4× m;
d2 = m× z2; da2 = d2 + 2× m× (1 + x); df2 = d2 - 2× m× (1, 2 - x);
и наибольший диаметр колеса dам2* £ da2+ 6× m / (z1+2);
- длину b1 нарезной части червяка и ширину b2 зубчатого венца колеса:
при z1=1 или 2... b1*≈ 0, 03× m× (122+× z2)× [2+ 3√ ( x+0, 6)2]+25 мм и b2* £ 0, 75× da1,
при z1= 4..... b1*≈ 0, 02× m× (122+× z2)× [4+3√ (x+0, 6)2]+25 мм и b2* £ 0, 67× da1;
- угол подъема витка червяка начальный gW = Arctg [z1/ (q+2× x)];
- окружную скорость колеса v2 =p× d2× n2/(60× 103) м/с;
- скорость скольжения в зацеплении фактическую vs=v2/sin gW, .
Уточнить КПД червячного редуктора hч =0, 97× tg gW / tg (gW+r), где r »(2, 9/√ vs+0, 3)о при-веденный угол трения в зацеплении. При существенном отличии hч от ранее принятого значения (см. энергосиловой расчет привода) уточнить: КПД привода, мощности Р1 и Р0 и вращающие моменты Т1 и Т0 на соответствующих валах и, возможно, типоразмер двигателя.
Найти силы в зацеплении, действующие на червяк и колесо: окружные Ft1= 2000× T1/d1 и Ft2=2000× T2/d2; радиальные Fr1 = Fr2 » Ft2 × tg 20◦ и осевые Fa1 = Ft2 и Fa2 = Ft1 в Н.
5.2. Проверочный расчет передачи на контактную прочность
Исходные данные: Ft2; d2; d1; z2; q; x; m; v2; nст; [s]H; график нагружения: θ i, λ i.
Цель расчета – проверка материалов и размеров передачи из условия контактной прочности (износостойкости) зубьев колеса: [ s ] H ³ s H = 335 × √ Ft 2 ∙ kβ ∙ kv /[ d 2∙ ( d 1 + 2∙ x ∙ m )] МПа,
где kb - коэффициент концентрации нагрузки: kb =1 + (z2/θ Ч)3 × (1 - Σ θ i ∙ λ i),
здесь θ Ч ≈ 9∙ (q–4)∙ (1 + 1/z1) - коэффициент деформации червяка;
kv- коэффициент динамичности: kv = 1 при v2≤ 3 м/с, иначе - kv = 1 + 3∙ 10-3∙ v2∙ (nст - 2).
Сделать вывод о контактной прочности ЧП, допуская перегрузку до 5% и недогрузку до 20%, иначе - доработать конструкцию ЧП, изменив: - либо материал ЧП, - либо размеры ЧП, приняв а w ≈ а w ∙ (σ H/[σ ]H)2/3; и повторить соответствующие расчеты.
5.3. Проверочный расчет передачи на и згибную выносливость
Исходные данные: Ft2, m, q, x, z2, gW, kb, kv, [s]F.
Цель расчета – проверка материалов и размеров передачи из условия изгибной выносливости (усталостной прочности) зубьев колеса: [ s ] F ³ s F = Ft 2 × k b × kv × cos g W × YF / [1, 3 × m 2 × ( q + 2· x )] МПа,
где YF – коэффициент формы зуба колеса: YF » 1, 2 + 15·cos3 gW / z2 .
Сделать соответствующий вывод об изгибной выносливости ЧП, а при необходимости изменить ее конструкцию указанными выше способами – см. п. 5.2.
5.4. Проверочный расчет червячного редуктора на теплостойкость
Исходные данные: Р1, hЧ, а w , t0=20 0 C – температура окружающей среды.
Цель расчета – обеспечение теплостойкости и, следовательно, сохранение нагрузочной способности редуктора установленных размеров по условию
t 0 p = t 0 0 + 103∙ P 1 (1–η Ч) / [ Ap ∙ kt · (1+ψ )] ≤ [ t 0 ] M ° C,
где t0p и [t0]M – температура, установившаяся, редуктора и допускаемая для масла:
[t0] M ≈ 90° C – для минеральных масел, [t0] M ≈ 120°С – для синтетических;
Ap – площадь поверхности охлаждения редуктора,
для одноступенчатого редуктора Ap»12∙ а w 1, 7 м2 ( здесь а w в м );
kt – коэффициент теплоотдачи в Вт/(м2· 0С): kt≈ 16±5 при естественном охлаждении,
kt≈ 40±10 при воздушном охлаждении, kt≈ 150±50 при водяном охлаждении;
ψ – коэффициент увеличения поверхности охлаждения через плиту (раму): ψ »0, 3.
Выбрать соответствующие способ охлаждения редуктора (отразить в конструкции) и марку масла для смазки передачи [4], обеспечив теплостойкость и сохранение нагрузочной способности редуктора.
При vS< [v]S проверить возможность применения для венца колеса более дешевого материала по условиям износостойкости и прочности зубьев [s]H (F) ³ sH (F).
Выполнить эскиз ЧП, с указанием принятых размеров, например, см. рис. 5.1.
.
* Размеры b 1, b 2 и dam 2 задавать целыми числами.
- 14 -
Пример 5п. Расчеты червячной передачи одноступенчатого редуктора
5.1п. Проектный расчет передачи
Исходные данные: Т2=460 Нм; n1=1460 об/мин; n2=58 об/мин; u=25; P2=2, 73 кВт;
Lh=8000 час; график нагружения постоянный: θ 1=1, λ 1=1.
Цель расчета – обоснование материалов и размеров ЧП, удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям.
Задаем материал червяка - сталь 45 с закалкой витков ТВЧ HRC 50…53 и их последующей шлифовкой и полировкой. Задаем материал зубьев колеса с учетом ожидаемой скорости скольжения в зацеплении vS'≈ ≈ 0, 45∙ 10-3∙ n1∙ 3√ T2 = 0, 45∙ 10-3∙ 1460∙ 3√ 460 = 5, 1 м/с. Принимаем (табл. 5.1) бронзу БрО10Ф1 - литье в кокиль, для которой допустимая скорость скольжения [ns]=12 м/с > vS', σ т=195 МПа и σ в=245 МП.
Определяем допускаемые напряжения (табл. 5.1) контактной [s]H и изгибной [s]F выносливости зубьев колеса [σ ]н=0, 9∙ σ в∙ 8√ 107/NHE и [σ ]F=(0, 25·σ т + 0, 08·σ в)∙ 9√ 106/NFE,
где NHE и NFE – эквивалентные числа циклов зубьев,
для постоянного графика нагружения NHE = NFE = 60∙ n2∙ Lh = 60∙ 58∙ 8000≈ 2, 7·107 < 25·107.
При этом [ σ ]н =0, 9∙ 245∙ 8√ 107/2, 7·107 = 195 МПа и [ σ ] F =(0, 25·195+0, 08·245)∙ 9√ 106/2, 7·107 = 47 МПа.
Определяем ожидаемое межосевое расстояние передачи, приняв коэффициент нагрузки kн≈ 1, 1
aw′ =610∙ 3√ T2·kн /[σ ']н 2 = 610∙ 3√ 460·1, 1 /1952 = 144, 5 мм, принимаем aw = 145 мм .
Принимаем число заходов червяка z 1 = 2, соответствующее u=25, и определяем диапазон приемлемых чисел зубьев колеса z '2 min ≥ 0, 96·u·z1=0, 96·25·2= 48 и z '2 max ≤ 1, 04·u·z1≤ 1, 04·25·2= 52;
Принимаем:
- коэффициент диаметра червяка из условия q ≥ 0, 2× z2MIN = 0, 2× 48 = 9, 6, принято q = 10;
- модуль зацепления из диапазона m ≤ 2·a w /(z2MIN+ q±2)= 2·145 / (48 + 10 ±2)=4, 8…5, 2 мм, принято m = 5 мм;
- число зубьев колеса из установленного диапазона, дополненного ограничениями z2 = 2· aw/m – q ± 2 = =2·145/5 – 10 ± 2= 46…50, т.е. приемлемо любое число зубьев из фактического диапазона z2=48…50.
Принято ближайшее к u·z1=50 значение: z 2 =50.
Определяем:
- коэффициент смещения червяка x = aw/m–(z2+q)/2=145/5-(50+10)/2= -1, что удовлетворяет условию +1³ x ³ - 1;
- делительные диаметры d1(2) витков червяка (зубьев колеса), диаметры da1(2) их выступов и df1(2) – впадин:
d 1 =m× q=5·10= 50 мм, da1=d1+2× m=50+2× 5= 60 мм, d f1=d1-2, 4× m=50-2, 4× 5= 38 мм;
d 2 =m× z2=5·× 50= 250 мм, da2=d2+2× m× (1+x)=250+2× 5·(1-1)= 250 * мм; d f2=d2-2× m× (1, 2-x)=250-2× 5·(1, 2+1)= 228 мм;
- наибольший диаметр колеса d a m2 = d a 2+6× m/(z1+2) = 250+6× 5/(2+2) ≈ 258 мм;
- длину b 1 нарезной части червяка и ширину b 2 зубчатого венца колеса .
b 1 = 0, 03× m× (122+z2)× [2 + 3√ (х+0, 6)2]+25 = 0, 03× 5× (122+50)× [2+ 3√ (-1+0, 6)2]+25 ≈ 90 мм,
b 2 £ 0, 75·d a 1 = 0, 75× 60 = 45 мм;
- угол подъема витка червяка начальный gW = Аrctg [z1/ (q+2× x)] = Аrctg [2/(10 - 2× 1)] ≈ 14о;
- окружную скорость колеса v2 = p× d2× n2/(60× 103) = p× 250× 58/(60× 103) = 0, 76 м/с;
- скорость скольжения в зацеплении фактическую vs = v2/sin gW = 0, 76/sin 14о = 3, 1 м/с < [ns] = 12 м/с,
по которой принимаем соответствующую степень точности передачи nст = 8.
Уточняем:
- КПД червячного редуктора hч = 0, 97× tg gW / tg (gW+r),
где r – угол трения в зацеплении, .
при r = 2, 9/√ vs+0, 3 = 2, 9/√ 3, 1+0, 3 = 1, 6о получаем hч = 0, 97× tg 14 о/tg (14 о+1, 6о) = 0, 87;
- мощность на валу червяка Р1 = Р2/hч = 2, 73/0, 87 = 3, 14 кВт;
- вращающий момент на валу червяка Т1 = Т2 /(uф·hч) = 460/(25·0, 87) = 21, 1 Нм;
- общий КПД привода с червячным редуктором (см. п. 1, для схемы 4) η ПР = η м·η ч·η м = 0, 98·0, 87·0, 98 ≈ 0, 84;
- силы в зацеплении, действующие на червяк и колесо:
окружные Ft1 = 2000× T1/d1 = 2000× 21, 1/50 = 844 Н и Ft 2 = 2000× T2/d2 = 2000× 460/250 = 3680 Н;
радиальные Fr1 = Fr2 ≈ Ft2× tg 20о = 3680× tg 20о = 1340 Н, и осевые F a 1 = Ft2 = 3680 Н и F a 2 = Ft1 = 844 Н.
.
* Здесь получено d2 = d a 2 = 250 мм, что неизбежно при x = - 1.
- 15 -
5.2п. Проверочный расчет передачи на контактную прочность
Исходные данные: Ft2=3680 Н; d2=250 мм; d1=50 мм; z2=50; q=10; x= - 1; m=5 мм;
v2=0, 76 м/с; nст=8; [s]H=195 МПа; график нагружения постоянный.
Цель расчета - проверка материалов и размеров передачи из условия контактной прочности (износостойкости) зубьев колеса: [s]H ³ sH = 335× √ Ft2∙ kβ ∙ kv/[d2∙ (d1+2∙ x∙ m)] МПа,
где kb - коэффициент концентрации нагрузки, принимаем kb= 1, т.к. график нагружения постоянный;
kv - коэффициент динамичности, принимаем kv = 1, т.к. скорость колеса v2< 3 м/с.
При этом s H = 335× √ 3680∙ 1∙ 1/[250·(50 - 2∙ 1·5)] = 203 МПа, что больше, чем [s]H = 195 МПа на 4% при допустимой перегрузке 5%, следовательно, контактная прочность передачи приемлема.
5.3п. Проверочный расчет передачи на изгибную выносливость
Исходные данные: Ft2=3680 Н; m=5 мм; x= - 1; z2=50; q=10; gW=14о; kb=1; kv=1; [s]F=47 МПа.
Цель расчета - проверка материалов и размеров передачи из условия изгибной выносливости зубьев колеса:
[s]F ³ sF = Ft2× kb× kv× cos gW× YF / [1, 3× m2× (q+2·x)] МПа,
где YF – коэффициент формы зуба колеса, YF = 1, 2+15·cos3 gW / z2 = 1, 2+15·cos3 14о / 50 = 1, 47.
При этом s F = 3680× 1× 1× cos 14о× 1, 47 / [1, 3 × 52× (10 - 2·1)] = 18 МПа, что меньше, чем [s]F = 47 МПа, следовательно, изгибная выносливость зубьев колеса также обеспечена.
5.4п. Проверочный расчет червячного редуктора на теплостойкость
Исходные данные: Р1=3, 14 кВт; hЧ=0, 87; a w =0, 145 м ; t0=20 0 C – температура окружающей среды.
Цель расчета – определение марки масла для смазывания червячного зацепления и способа охлаждения редуктора, обеспечивающих его теплостойкость и нагрузочную способность из условия
tp = t0 + 103∙ P1·(1 – η Ч) / (Ap∙ kt·1, 3) ≤ [t]M,
где tp и [t]M – температура, установившаяся, редуктора и допускаемая для масла;
Ap – площадь поверхности охлаждения редуктора, Ap » 12∙ a w 1, 7=12·0, 1451, 7 = 0, 45 м2 (здесь aw в м);
kt – коэффициент теплоотдачи, принимаем kt=16 Вт/(м2·оС) для естественного охлаждения редуктора.
При этом tp = 20 +103∙ 3, 14·(1 – 0, 87) / (0, 45∙ 16·1, 3) = 64 0 С .
Принимаем для смазки червячной передачи масло индустриальное ” И-Г-А 32 ”, у которого [ t ] M ≈ 90о C > > tp=69оС, при этом теплостойкость редуктора в условиях естественного охлаждения будет обеспечена и сохранена его нагрузочная способность.
Следовательно, работоспособность передачи установленных размеров для колеса из бронзы БрО10Ф1 обеспечена по всем расчетным критериям. Отмечаем, что скорость скольжения в зацеплении vs = 3, 1 м/с допускает возможность изготовления колеса из более дешевой латуни ЛАЖМц66-6-3-2, для которой [ n s ] = 4 м/с > vs, σ т = 295 МПа и σ в = 450 МПа. Проверим эту возможность по критериям износостойкости и прочности передачи, определив допускаемые напряжения [σ ]н(F) для ЛАЖМц66-6-3-2 (табл. 5.1) и сравнив их с найденными фактическими напряжениями σ н(F), соответствующими установленным размерам и нагрузке передачи:
[σ ]н = 300 - 25·vs = 300 - 25 ·3, 1 = 222 МПа > s H = 203 МПа, .
[ s ] F = (0, 25·sт + 0, 08·sв) ∙ 9√ 106/NFE = (0, 25·295 + 0, 08·450) ∙ 9√ 106/ 2, 7·107 = 76 МПа > s F = 18 МПа,
что также удовлетворяет условиям прочности.
Окончательно назначаем материал колеса ЛАЖМц66-6-3-2 (отливка в кокиль) и червяка - сталь 45 (закалка ТВЧ, HRC 50…53), что гарантирует работоспособность передачи установленных размеров (рис. 5.1) по всем расчетным критериям в заданных условиях эксплуатации.
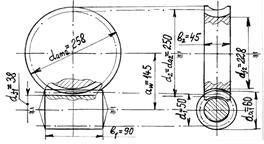
Рис. 5.1
- 16 -
6. Расчет цепной передачи (ЦП) с роликовой цепью
Исходные данные: Т1; Kп; n1; u; [ a'; γ '; D 1мах или D 2мах ≤ 1, 2· Dбарабана ; … ]; условия работы ЦП.
Цель расчета – обоснование условий эксплуатации и основных размеров ЦП с роликовой цепью (ГОСТ 13568-75), удовлетворяющих заданным параметрам, критериям работоспособности и конструктивным требованиям при ресурсе цепи не менее 3000 ч.
Расчетом определяют размеры ЦП либо рекомендуемые [ 1 ], либо – с учетом конструктивных ограничений межосевого расстояния а, угла γ наклона ЦП и делительных диаметров D 1(2) звездочек, соответствующих рациональной компоновке привода (например, в курсовом проекте ДМ). Учет этих ограничений приведен в скобках [курсивом] в соответствующих разделах расчета.
Определить коэффициент KЭ условий эксплуатации (износостойкости) ЦП, соответствующий ресурсу цепи не менее 3000 час K Э = К VA ·Ка∙ Крег∙ К γ ∙ Ксм∙ Крр ≤ 3,
где КVA – коэффициент динамичности машины: КVA = 1 – при плавной работе машины,
КVA ≈ 1, 3 – при работе толчками, КVA ≤ 1, 8 – при работе с ударами;
Кa – коэффициент межосевого расстояния a, зависящий от шага t цепи:
Кa = 1 для диапазона a =(30…50)t; иначе - Кa= ³ √ 40∙ t/a при ограничениях 0, 8≤ Кa≤ 1, 25,
первично принять К ' a = 1 [при заданном a ' в дальнейшем коэффициент К' а д. б. уточнен];
Крег– коэффициент регулировки провиса цепи: Крег=1 при наличии регулировки; иначе – Крег=1, 3;
Кγ – коэффициент угла γ наклона ЦП к горизонту: Кγ = 0, 15∙ √ γ ≥ 1 (при γ ≤ 45º … Кγ =1);
Ксм – коэффициент смазки цепи: Ксм=1 – при постоянной смазке, Ксм=1, 5 – при периодической;
Крр – коэффициент числа m смен работы ЦП: КРР = ³ √ m;
При KЭ > 3 необходимо принять конструктивные меры по улучшению условий эксплуатации ЦП.
Определить ожидаемый шаг цепи t ' ≈ 29∙ ³ √ Т1·КЭ / ( z 1 ·[ p ]·К r ) мм,
где z1 – число зубьев малой звездочки, первично принять z′ 1 ≈ 29 – 2·u ≥ 15, но не более z′ 1 ≤ 120 /u;
[p] – допускаемое давление в шарнире цепи, первично принять [p′ ] = 110 / 4√ n1 ≤ 35 МПа;
Кr – коэффициент числа r рядов цепи (r≤ 3): Кr=r0, 8, первично принять число рядов r′ =1 и К′ r=1.
Значение t' округлить до стандартного t (с учетом возможных ограничений по частоте враще-ния n1≤ nрек(пр)) и принять соответствующие выбранной цепи площадь А шарнира, разрушающую силу F р зр и уточненное значение допускаемого давления [ p ] в шарнире цепи (табл. 6.1).
Таблица 6. 1
|
Обозначение Цепи | t мм | A | F р зр | * n рек | * n пр | [ p ] в МПа при n 1 об/мин (для Кэ=1 и z1=15…30) | |||||||
| мм 2 | Кн | об/мин | ≤ 50 | 200 | 400 | 600 | 800 | 1000 | 1200 | 2400 | |||
| ПР-12, 7-1820 | 12, 7 | 40 | 18, 2 | 1250 | 3150 | 35 |
31, 5 |
28, 5 | 26 | 24 | 22, 5 | 21 | 1, 5 |
| ПР-15, 875-227 | 15, 875 | 71 | 22, 7 | 1000 | 2300 | ||||||||
| ПР-19, 05-3180 | 19, 05 | 105 | 31, 8 | 900 | 1800 | 35 | 30 | 26 |
23, 5 | 21 | 19 |
17, 5 | |
| ПР-25, 4-5670 | 25, 4 | 180 | 56, 7 | 700 | 1200 | ||||||||
| ПР-31, 75-8850 | 31, 75 | 260 | 88, 5 | 500 | 1000 | 35 | 29 | 24 | 21 | 18, 5 | 16, 5 | ||
| ПР-38, 1-12700 | 38, 1 | 395 | 127, 0 | 400 | 900 | ||||||||
| ПР-44, 45-17240 | 44, 45 | 475 | 172, 4 | 300 | 600 | 35 | 26 | 21 | 17, 5 | - | - | ||
| ПР-50, 8 - 22680 | 50, 8 | 645 | 226, 8 | 250 | 450 | ||||||||
* Наибольшие частоты вращения малой звездочки: рекомендуемая – nрек и предельная – nпр.
Уточнить: - числа зубьев* звёздочек, при которых гарантирована износостойкость цепи выбранного типоразмера z1 ≥ 6, 3·103·Т1·КЭ/(t·A·[p])≥ 15 и z2≈ z1·u ≤ 120
[при заданном а' использовать уточненные значения коэффициентов К а =³ √ 40∙ t/a ' и КЭ =К ' Э∙ Ка – см. выше];
- передаточное число ЦП = z2/z1 (допустимо отклонение от заданного u до 4%);
Определить: - делительные диаметры звездочек D 1(2) = t / sin (180º /z1(2)) мм;
- скорость цепи υ ц= π ·D1·n1 / 60000 ≤ 15 м/сек;
- окружную силу на звездочках Ft = 2000·T1 / D1 H;
Оценить прочность цепи, сопоставив запасы прочности nц- фактический и [n]ц– допустимый: n ц ≈ Fрзр·Кr/(1, 05·Ft·Kп) ≥ [ n ] ц =5, а при неудовлетворительном результате [или при D1(2)> D1(2)мах] изменить в конструкции ЦП шаг t или рядность r цепи; и повторить соответствующие расчеты.
Определить: - длину цепи в шагах Lt≈ 2·a/t+(z1+z2)/2+[(z2–z1)/2·π ]2·t/a, здесь использовать заданное а' или принять рекомендуемое а ≈ 40·t; Lt округлить четным числом;
- длину цепи фактическую, L ц = Lt·t мм; .
- межосевое расстояние ЦП, а = 0, 997·t∙ [Lt–(z1+z2)/2+√ [Lt–(z1+z2)/2]2–2·[(z2–z1)/π ]2] / 4 мм;
- силу на валы при работе ЦП, F ц п ≈ 1, 05·Ft Н.
Вывод: ЦП установленных размеров работоспособна в заданных условиях эксплуатации.
Варьируя шаг и рядность цепи м.б. найдены иные приемлемые варианты ЦП, из которых предпочтителен вариант с цепью меньшего шага и рядности, соответствующий целесообразной конструкции привода. При конструировании ЦП задавать тяговую ветвь цепи верхней.
* Желательно задавать z 1 и z 2, некратными числами.
- 17 -
Пример 6п. Расчет цепной передачи с роликовой цепью (ГОСТ 13568-75)
Исходные данные: Т1=180 Нм; Kп=1, 5; n1=150 об/мин; u=3;
Проектные условия эксплуатации передачи: нагрузка привода равномерная; работа односменная; межосевое расстояние передачи обеспечить в рекомендуемом диапазоне a=(40±10)·t; провис цепи регулировать передвижением малой звездочки; угол наклона передачи к горизонту γ ≈ 60о; смазка цепи периодическая; ограничения по величине диаметров D1(2) звездочек отсутствуют.
Цель расчета – обоснование условий эксплуатации и основных размеров ЦП, удовлетворяющих исходным параметрам, критериям работоспособности и конструктивным требованиям при ресурсе цепи не менее 3000 ч.
Определяем коэффициент условий эксплуатации передачи KЭ= КVA· Кa ∙ Крег∙ Кγ ∙ Ксм∙ Крр ,
где КVA– коэффициент динамичности машины;
Кa – коэффициент межосевого расстояния a, зависящий от шага t цепи;
Крег – коэффициент регулировки провиса цепи;
Кγ – коэффициент угла γ наклона передачи к горизонту;
Ксм -коэффициент смазки цепи;
Крр – коэффициент числа m смен работы передачи.
Принимаем рекомендуемые значения коэффициентов, соответствующие заданным условиям эксплуатации передачи: КVA=1 - при равномерной нагрузке привода; Кa=1 - при рекомендуемой величине межосевого расстояния a=(30…50)·t; Крег =1 - при регулировании провиса цепи; Кγ = 0, 15∙ √ γ = 0, 15∙ √ 60 = 1, 16 - при угле наклона передачи к горизонту γ = 60о; Ксм = 1, 5 - при периодической смазке цепи; Крр =1 - при односменной работе m =1.
При этом K Э = 1·1∙ 1∙ 1, 16∙ 1, 5∙ 1 = 1, 74 < [KЭ] = 3, т.е. условия эксплуатации передачи приемлемы.
Определяем ожидаемый шаг t ' цепи, приняв ожидаемые число зубьев малой звездочки z'1 = 29 - 2·u = =29 - 2·3 = 23 > 120/u=120/3=40, допускаемое давление в шарнире цепи [p'] = 110 / 4√ n1 =110 / 4√ 150 = 31, 4 МПа и коэффициент рядности К r = 1 при числе рядов цепи r = 1, .
при этом t'= 29∙ ³ √ Т1·КЭ /(z1·[p]·Кr) = 29∙ ³ √ 180·1, 74 / (23·31, 4·1) = 21, 9 мм.
Округляем t' до ближайшего стандартного значения t = 19, 05 мм (цепь ПР-19, 05-3180 ГОСТ 13568-75), и принимаем (табл. 6.1) соответствующую площадь шарнира А=105 мм2, разрушающую силу Fрзр=31800 Н и допускаемое давление в шарнире цепи [ p ]= 31, 7 МПа (найдено интерполированием по данным табл. 6.1).
Уточняем числа зубьев звёздочек, гарантирующие износостойкость цепи
z 1 ≥ 6, 3·103·Т1·КЭ / (t·A·[p]·Kr) = 6, 3·103·180·1, 74 / (19, 05·105·31, 7·1) ≈ 32,
z 2 ≈ z1·u =32·3≈ 95 < [120] (z2 принято нечетным числом при четном z1),
при этом передаточное число u= z2/z21= 95/32= 2, 97, что отличается от заданного на 1%.
Определяем:
- делительные диаметры звездочек
D1 = t / sin (180º / z1) =19, 05 / sin (180º / 32 ≈ 194 мм ,
D2 = t / sin (180º / z2) =19, 05 / sin (180º / 95) ≈ 576 мм;
размеры зубьев звездочек по ГОСТ 591-69;
- скорость цепи vц = π ·D1·n1 / 60000 = π ·194, 4·150 / 60000 = 1, 5 м/сек ≤ [v] = 15 м/сек;
- окружную силу в передаче Ft = 2000·T1 / D1 = 2000·180 / 194, 4= 1852 H;
Оцениваем прочность цепи, сопоставляя запасы прочности фактический nц и допускаемый [n]ц = 5:
n ц = Fрзр·Кr / (1, 05·Ft· Kп) = 31800·1 / (1, 05·1852·1, 5) = 10, 9 > [n]ц, следовательно прочность цепи обеспечена.
Определяем прочие характеристики передачи:
- длину Lt цепи в шагах t, приняв ожидаемое межосевое расстояние рекомендуемым значением
a ' = 40·t = 40·19, 05 ≈ 762 мм, при этом Lt = 2·a ' / t + (z1 + z2) / 2 + [(z2 – z1) /(2·π )]2·t / a ' =
= 2·762 / 19, 05 + (32+95) / 2 + [(95-32) / (2·π )]2·19, 05 / 762 ≈ 146;
- длину цепи L ц = Lt·t = 146·19, 05 = 2781 мм; .
- межосевое расстояние a = 0, 997·t∙ [ Lt – (z1 + z2) / 2 + √ [Lt – (z1 + z2) / 2]2 – 2·[(z2 – z1) / π ]2 ] / 4 =
= 0, 997·19, 05∙ [ 146–(32+ 95)/2+√ [146–(32+95)/2]2–2·[(95-32)/π ]2 ] / 4 = 760 мм .
Выполненные расчеты свидетельствуют о работоспособности цепной передачи установленных размеров с цепью ПР-19, 05-3180 ГОСТ 13568-75 в заданных условиях эксплуатации с ресурсом не менее 3000 час, при этом сила на валы при работе передачи составляет F цп ≈ 1, 05·Ft = 1, 05·2194 = 2300 Н .
ЮМ_2012
- 18 -
7. Расчет клиноременной передачи (РП)
Исходные данные: Р1; T1; n1; u; [ a'; D1(2)мах ]; условия работы передачи.
Цель расчета – обоснование основных размеров РП с клиновыми ремнями (ГОСТ 1284-80), удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям при ресурсе ремней не менее 2000 час.
Расчетом определяют размеры РП либо рекомендуемые [1], либо – с учетом ограничений межосевого расстояния a и диаметров шкивов D 1(2) max , соответствующих рациональной компоновке и соразмерности узлов привода, например, в курсовом проекте ДМ. Учет этих ограничений приведен в скобках [курсивом] в соответствующих разделах расчета.
Выбрать сечение клиновых ремней (ГОСТ 1284-80), диапазон крутящих моментов T1Σ которых соответствует передаваемому T1, и выписать значение базовой длины ремня L 0 ( табл. 7.1).
Таблица 7.1
| Сечение ремня * ГОСТ1284-80 | b x h мм∙ мм | LMIN мм | LMAX мм | L 0*2 мм | D 1*1MIN Мм | T 1Σ Нм | |
|
| Z | 10 х 6 | 400 | 2500 | 800 | 63 | < 25 |
| A | 13 х 8 | 560 | 4000 | 1700 | 90 | 11…70 | |
| B … | 17 х 11 | 800 | 6000 | 2240 | 125 | 40…190 | |
3.
*1 Ряд диаметров D 1(2) шкивов: 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400, 450, 500, 560, 630, 710 и далее по ряду Ra40.
*2 L 0 - базовая длина ремня, соответствующая ряду стандартных длин L: 400, 450, 500, 560, 630, 710, 800 и далее по ряду Ra40.
Принять стандартное значение диаметра D 1 ≥ D1MIN меньшего шкива (табл. 7.1) [учесть ограничение D 1 ≤ D 2 max / u], и проверить его приемлемость по скорости ремня υ = π ·D1·n1/60000 < < [υ ]*=25…30 м/с.
Определить:
- стандартный диаметр большего шкива D2≈ D1·u;
 - длину ремня L≈ 2·a'+π · (D2+ D1)/2+(D2–D1)2/(4·a')
- длину ремня L≈ 2·a'+π · (D2+ D1)/2+(D2–D1)2/(4·a')
[здесь использовать рекомендуемое межосевое рассто-яние a'≈ 0, 75·(D1+D2) или заданное значение а' ];
округлить L до стандартного значения (табл. 7.1);
- фактическое межосевое расстояние .
а = [2·L–π ·(D2+D1)+√ [2·L–π ·(D2+D1)]2–8·(D2–D1)2]/8;
- угол охвата ремнем малого шкива
α 1 = 180º – 57º ·(D2 – D1)/ а ≥ [α 1]=120º (70º )**;
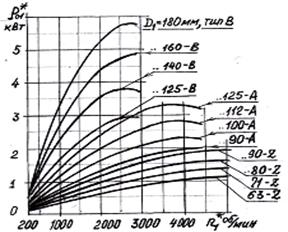
- значение базовой мощности P01* (рис. 7.1), переда- ваемой одним ремнем выбранного сечения и базовой длины L0 на шкивах диаметром D1 (u=1, α 1=1800) при
плавной работе с заданной частотой вращения n1 при ресурсе ремня не менее 2000 час;
- число ремней ZР (целое) с учетом степени неравномер- ности их натяжения, равной 1, 07
ZР* * * ≥ ZР'= P1/(P 01·Сα ·СL·Cu·Cpp)1, 07, .
где Сα - коэффициент угла α 1 охвата, Сα ≈ √ (α 1–10 º )/170º ; Рис. 7.1
СL - коэффициент длины ремня, СL ≈ 6√ L /L0 ;
Cu - коэффициент передаточного числа, Cu ≈ 1, 14–0, 14/u4;
Cpp- коэффициент режима работы (динамичности): Cpp =1 при плавной работе,
Срр ≈ 0, 85 при работе толчками, Cpp ≈ 0, 65 при работе с ударами.
Вывод: РП установленных размеров работоспособна в заданных условиях эксплуатации с ресурсом не менее 2000 час. При этом сила на валы при работе передачи составляет
FРП ≈ 1700·P1·CL·Cu·cos (90o- α 1/2) / (υ ·Сα ·Cpp) Н.
Аналогично м.б. обоснованы иные варианты РП (т.к. многовариантен выбор и сечения ремня и D1(2) шкивов), из которых м.б. принят рациональный по массе, нагрузкам FРП и компоновке привода.
.
* Более полные характеристики РП см. ГОСТ 1284-80.
** В скобках приведены экстремальные значения соответствующих характеристик.
*** Если при округлении числа ремней получено Z Р - Z ' > 0, 5, то проверить целесообразность следующих вари- антов: - либо изменить D1(2), сохранив сечение ремня; - либо изменить и сечение ремня и, возможно, D1(2).
- 19 -
Пример 7п. Расчет клиноременной передачи
Исходные данные: Р1=2, 9 кВт; T1=19, 4 Нм; n1=1430 об/мин; u=2, 5;
Условия работы: работа передачи плавная;
желательны минимальные габариты передачи.
Цель расчета – обоснование основных размеров РП с клиновыми ремнями (ГОСТ 1284-80), удовлетворяющих исходным данным, критериям работоспособности и конструктивным требованиям передачи при ресурсе ремней не менее 2000 час.
Выбираем клиновые ремни сечения А (ГОСТ 1284-80), диапазон крутящих моментов которых Т1Σ =11…70 Нм соответствует передаваемому моменту T1=19, 4 Нм, при этом базовая длина ремней L 0 =1700 мм (табл. 7.1).
Принимаем диаметр меньшего шкива D 1 = D1MIN = 90 мм (табл. 7.1) т.к. желательны минимальные габариты передачи, при этом скорость ремня υ = π ·D1·n1/60000 = π ·90·1430/60000 = 6, 7 м/с < [υ ] = 25 м/с.
Определяем:
- стандартный диаметр большего шкива D 2 = D1·u = 90·2, 5 ≈ 224 мм (табл. 7.1);
- межосевое расстояние рекомендуемое a ' = 0, 75·(D1 + D2) = 0, 75·(90 + 224) ≈ 236 мм;
- длину ремня ожидаемую L' = 2·a '+π ·(D2 + D1) / 2 + (D2 – D1)2 / (4·a ') =
= 2·236 + π ·(90 + 224) / 2 + (224 – 90)2 / (4·236) = 983 мм,
и фактическую L, с округлением L' до стандартного значения L = 1000 мм (см. примечание к табл. 7.1);
- межосевое расстояние фактическое a = [2·L – π ·(D2 + D1)+√ [2· L – π ·( D 2 + D 1 )]2 – 8·( D 2 – D 1 )2 ] / 8 =
= [2·1000–π ·(224+90)+√ [2·1000π ·(224+90)]2–8·(224–90)2 ] / 8 = 244 мм;
- угол охвата ремнем малого шкива α 1 = 180º –57º ·(D2 – D1)/a =180º –57º ·(224–90) / 244= 149о > [α 1]= 120º.
Принимаем значение базовой мощности P01=1, 1 кВт (рис. 7.1), передаваемой одним ремнем сечения А базовой длины L0=1700 мм на шкивах диаметром D1=D2=90 мм при плавной работе с частотой n1=1430 об/мин и ресурсе ремней не менее 2000 час.
Определяем число ремней
ZР = P1/(P01·Сα ·СL·Cu·Cpp)1, 07, .
где Сα – коэффициент угла α 1 охвата, Сα = √ (α 1 –10 º )/170º = √ (149–10)/170 = 0, 9,
СL – коэффициент длины ремня, СL= 6√ L /L0 = 6√ 1000/1700 = 0, 92,
Cu – коэффициент передаточного числа, Cu=1, 14–0, 14/u4 =1, 14–0, 14/2, 54 ≈ 1, 14,
Cpp – коэффициент режима работы, Cpp=1 при плавной работе;
при этом Z Р =2, 9/(1, 1·0, 9·0, 92·1, 14·1)1, 07 ≈ 3.
Следовательно, передача установленных размеров с тремя ремнями А-1000 Т ГОСТ 1284-80 на шкивах D1(2)= 90(224) мм обладает достаточной надежностью в пределах ресурса не менее 2000час., и при ее работе сила на валы передачи составляет
F РП = 1700·P1·CL·Cu·cos (90o-α 1/2) / (υ ·Сα ·Cpp)=1700·2, 9·0, 92·1, 14·cos (90o-149o/2) / (6, 7·0, 9·1) = 826 Н.
.
Аналогично были выполнены расчеты (здесь не приводятся) иных приемлемых вариантов РП с ремнями сечения Z , диапазон крутящих моментов которых То1≤ 25 Нм также соответствует передаваемому Т1=19, 4 Нм. Результаты этих и предыдущего расчетов представлены в табл. 7.2, где Wшк - объем дисков шкивов.
Таблица 7.2
| Вариант | Сечение ремня | D1 (D2) Мм | L мм | a мм | υ м/с | P01 кВт | ZР - | FРП Н | Wшк дм3 |
| 1 | A | 90 (224) | 1000 | 244 | 6, 7 | 1, 1 | 3 | 811 | 0, 96 |
| 2 | Z | 90 (224) | 1000 | 244 | 6, 7 | 0, 9 | 4 | 920 | 0, 80 |
| 3 | Z | 80 (200) | 900 | 222 | 6, 0 | 0, 8 | 4 | 1016 | 0, 71 |
Анализ этих данных показал:
- при одинаковых габаритах передач (варианты 1 и 2) для РП с ремнями сечения Z характерно большее число ремней и большая консольная нагрузка на валы при меньшей массе шкивов, чем у РП с ремнями сечения А;
- возможно снижение найденных габаритов РП с применением ремней сечения Z и шкивов D1(2)=80 (200) мм (вариант 3), при этом на 35% снижается масса шкивов, но на 25% возрастает нагрузка на валы.
- выбор целесообразного варианта клиноременной передачи д.б. сделан по результатам сопоставления соответствующих конструкций привода по показателям материалоемкости, нагрузкам на валы и рациональности компоновки привода. При конструировании РП задавать тяговую ветвь ремня нижней.
- 20-
8. Выбор муфт и проектное обоснование диаметров валов и подшипников (ПК) редуктора
Исходные данные: схема привода, Т1(2), Кп, n1(2), dэ.
Цель расчета – обосновать тип и размеры стандартных муфт и ПК и диаметры валов.
Выбрать тип муфты согласно ее назначения. Например, в приводе конвейера, выполненного по схеме (рис. 8.1), целесообразно устанавливать компенсирующие муфты (при отсутствии требова- ний предохранения и управления приводом): на быстроходных валах муфту упругую втулочно-пальцевую (МУВП) или с резиновой звездочкой (МУЗ); на тихоходных – зубчатую (МЗ) или цепную (МЦ).
Выбрать  размеры стандартных муфт (табл. 8.1 … 8.4) по критериям: прочности – крутящий момент Тм муфты д. б. не менее момента на соединяемых валах - Тм ≥ ТMAX1(2) = Кп.Т1(2); быстроходности - nм ³ n1(2); собираемости – диаметры концов валов двигателя dэ и редуктора d1(2)М, соединяемых муфтами, должны совпадать с диаметрами dМ присоединительных отверстий полумуфт согласно их
размеры стандартных муфт (табл. 8.1 … 8.4) по критериям: прочности – крутящий момент Тм муфты д. б. не менее момента на соединяемых валах - Тм ≥ ТMAX1(2) = Кп.Т1(2); быстроходности - nм ³ n1(2); собираемости – диаметры концов валов двигателя dэ и редуктора d1(2)М, соединяемых муфтами, должны совпадать с диаметрами dМ присоединительных отверстий полумуфт согласно их
Рис.8.1 диапазонам (табл. 8.1 … 8.4); и соразмерности габаритов муфт и редуктора.
Принять диаметры валов редуктора под подшипниками d′ 1(2)ПК ≈ (5…7) · 3√ T1(2) (здесь Т1(2) в Нм; меньшие значения для тихоходных валов; d1(2)ПК обычно кратны 5), а под съемным колесом - d1(2)К принять с учетом технологичеких требований d1(2)К≥ d1(2)ПК ≥ d1(2)М.
Выбрать тип и схему установки подшипников (ПК) на валах, ориентируясь на узлы ПК в лучших аналогичных конструкциях редукторов [3], [4] (здесь используют разные типы ПК: радиальные шариковые (РШ) и роликовые (РР), радиально-упорные шариковые (РУШ) и роликовые (РУР) и др.). Размеры ПК выбранного типа первично легкой серии установить по диаметру d1(2)ПК вала.

В цилиндрических редукторах валы обычно монтируют на РШ * по схеме " враспор" (рис. 8.2), где каждый из ПК способен воспринимать одностороннюю осевую силу. В редукторах с шеврон- ными колесами один из валов (обычно быстроходный) делают " плавающим" в опорах на РР (рис. 8.3) для самоустановки вала по зубьям полушевронов.
В конических и червячных редукторах валы монтируют на РУР, обладающих высокой осевой жесткостью (или на РУШ), по схеме " враспор", а в опорах валов-червяков при опасности температур- ного защемления ПК применяют схему с одной " плавающей" опорой на РР (или РШ) и второй – " фиксирующей" на сдвоенных РУР (рис. 8.5). Валы с консольной конической шестерней обычно монтируют на РУР (или РУШ) по схеме " врастяжку" (рис. 8.4) для уменьшения габаритов редуктора.
Принятые проектные размеры валов, ПК, а также деталей передач использовать при разработке эскизного проекта редуктора и последующих проверочных расчетах валов, ПК, соединений, …, возможные неудовлетворительные результаты которых приводят к необходимости доработки конструкции редуктора (изменению материала или размеров валов, ПК, …) и повторению необходимых расчетов.
Пример 8п. Выбор муфт и проектное обоснование диаметров валов и ПК редуктора.
Исходные данные: схема привода – см. рис. 8.1; Т1(2) =85, 8(416)Нм; n1(2) =730(146)об/мин; dэ =48мм; Кп =1, 5.
Выбираем для заданной схемы привода стандартные компенсирующие муфты..
Для тихоходного вала находим: Тmax2 =1, 5.416 = 624 Нм и d ' 2ПК ≈ 5· 3√ T2= 5· 3√ 416= 37, 3 мм.
Примем** муфту зубчатую М3 - 1000 х 36 (табл. 8.3), у которой Тм=1000 Нм > Тmax2 ; nм =6300 об/мин > n2; и dм=36 мм (диапазон dм= 32…40 мм, длина lм =82 мм). Задаем*: диаметры ступеней тихоходного вала: d2М = 36 мм (длиной l2М =80 мм), d2ПК = 40 мм > d2М, d2К = 42 мм > d2ПК; и подшипники РШ 208 с установкой " враспор" .
Для быстроходного вала: Тmax1=1, 5.85, 8=129 Нм, dэ= 48 мм и d ' 1ПК≈ 7·3√ T1=7·3√ 85, 8=30, 8 мм.
Примем муфту МУВП – 250 х 48.1.1 х 32.1.2 (табл. 8.1), у которой: Тм=250 Нм> Тmax1, посадочные диаметры в полумуфтах разные dм=32 и 48 мм=dэ (диапазон dм=32…48 мм) и nм=3800 об/мин > n1. Задаем: диаметры* вала-шестерни d1М= 32 мм (l1М=58 мм) и d1ПК= 35 мм> d1М; подшипники 207 с установкой «враспор».
.
* В дальнейшем при недостаточном расчетном ресурсе РШ легкой серии заменяют на РШ средней серии или на РУР (реже на более дорогие, но быстроходные РУШ).
** Учитывая, что значение d'ПК ориентировочно, возможны иные варианты выбора, например, для тихо- ходного вала приемлем выбор муфты МЗ-1000х32, диаметров вала d2М=32 мм=dМ, d2ПК=35 мм; d2К=36 мм и подшипников 207 (таких же как у быстроходного вала) с установкой «враспор».
- 21 -
Таблица 8.1 Муфты упругие втулочно-пальцевые (МУВП) ГОСТ 21424-93*
| Тм Нм | nм мин-1 | Характеристики, мм | Dj=1, 50 | ||||||
| dм | lм** | Dм | D | z | Dr | ||||
| 31, 5 | 6350 | 16…18 | 40 / 28 | 63 | 90 | 4 | 0, 2 | ||
| 20…22 | 50 / 36 | ||||||||
| 63 | 5700 | 71 | 100 | 4 | 0, 2 | ||||
| 25…28 | 60 / 42 | ||||||||
| 125 | 4600 | 90 | 125 | 5 | 0, 3 | ||||
| 32…38 | 80 / 58 | ||||||||
| 250 | 3800 | 105 | 140 | 5 | 0, 3 | Dj=1, 00 | |||
| 40…48 | 110 / 82 | ||||||||
| 500 | 3600 | 130 | 170 | 5 | 0, 3 | ||||
| 50…56 | |||||||||
| 1000 | 2850 | 140 / 105 | 160 | 210 | 6 | 0, 4 | |||
| 63…70 | |||||||||
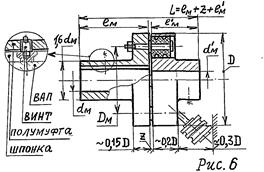
Таблица 8.2 Муфты с резиновой звёздочкой (МУЗ) ГОСТ 14084-76
| Тм Нм | nм мин-1 | Размеры, мм |
| |||||
| dм | lм** | Dм | D | B | ||||
| 31, 5 | 4000 | 16…18 | 40 / 28 | 52 | 71 | 18 | ||
| 20…22 | 50 / 36 | |||||||
| 63 | 3500 | 65 | 85 | 25 | ||||
| 25…28 | 60 / 42 | |||||||
| 3000 | 80 | 105 | 25 | ||||
| 32…38 | 80 / 58
| |||||||
| 250 | 2000 | 103 | 135 | 28 | ||||
| 40…48 | ||||||||
| 400 | 1500 | 38 | 125 | 166 | 33 | |||
| 40…48 | 110 /82 | |||||||
Таблица 8.3 Муфты зубчатые (МЗ) ГОСТ Р 50895-96
| Тм Нм | nм мин-1 | Размеры, мм |
| ||||||
| dм | lм | Dм | D | L | |||||
| 1000 | 6300 | 32…40 | 82 | 75 | 145 | 190 | |||
| 1600 | 5000 | 40…50 | 95 | 170 | |||||
| 2500 | 4800 | 40…60 | 105 | 100 | 185 | 245 | |||
| 4000 | 4300 | 50…65 | 110 | 200 | |||||
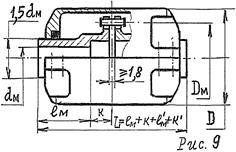 Таблица 8.4 Муфты цепные (МЦ) ГОСТ 20742-81*
Таблица 8.4 Муфты цепные (МЦ) ГОСТ 20742-81*
| Тм Нм | nм мин-1 | Характеристики, мм | Dj=10 | |||||
| dм | lм ** | k | Dм | D | Dr | |||
| 250 | 1200 | 32…38 | lМ** см.. МУВП | 23 | 98, 1 | 140 | 0, 2 | |
| 40…48 | 29 | |||||||
| 500 | 1020 | 29 | 142, 7 | 200 | 0, 4 | |||
| 780 | 50…56 | 30 | 147, 2 | 210 | 0, 4 | ||
| 2000 | 720 | 63…70 | 37 | 196, 3 | 280 | 0, 6 | ||
.
Примечания: 1.* ГОСТ… предусматривает не менее четырех типоразмеров муфт для монтажа на цилиндрических концах валов длинных lм11 и коротких lм12 по ГОСТ 12080-66, и на конических концах валов длинных lм21 и коротких lм22 по ГОСТ 12081-72:
| d м = dВ, мм | 16, 18, 19 | 20, 22, 24 | 25, 28 | 30, 32, 35, 36, 38 | 40, 42, 45, 48, 50, 55, 56 | 0, 63, 65, 70, 71, 75 |
| lм11 / lм12(21)-lм22, мм | 40/28-16 | 50/36-22 | 60/42-24 | 80/58-36 | 110/82-54 | 149/105-70 |
2.** В таблице значения lМ приведены для монтажа муфт только на цилиндрических концах валов: длинных- числитель, коротких– знаменатель.
3. Допускается компоновать муфты из полумуфт разных типов и с разными значениями lм и dм в указанных ГОСТ… пределах.
4. Смещения полумуфт не более: радиальное - Dr , угловое - Dj,, осевое - Dа ≈ 1 мм.
- 22 -
Последнее изменение этой страницы: 2019-03-30; Просмотров: 303; Нарушение авторского права страницы