СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ

 

Судовой энергетический комплекс состоит из разнообразных машин и механизмов, причем каждый из них может являться ОР. Один и тот же ОР может иметь несколько регулируемых параметров, независимых или связанных (взаимно влияющих друг на друга). Обычно ОР рассматривают с точки зрения одного заданного регулируемого параметра и учитывают при этом влияние на него остальных (если такое имеется). Так, паровой котел можно рассматривать как ОР давления пара либо уровня воды в барабане, а дизель - с точки зрения регулирования частоты вращения или температуры охлаждающей воды.

Характер протекания рабочих процессов зависит от свойств самого ОР и характера возмущений. Свойства ОР рассматриваются при условии, что объект управляется вручную, а возмущение наносится ступенчато в виде единичного скачка. Знание свойств ОР позволяет правильно выбрать тип регулятора и осуществлять его настройку. Поэтому обслуживающему персоналу, прежде всего, необходимо изучить свойства ОР и характер влияния их на качество процесса регулирования. При изучении можно использовать теоретические, расчетные либо экспериментальные данные (полученные при исследовании работы реального объекта или его модели).

Физическая сущность протекания процессов определяется из анализа уравнений динамики, отражающих аналитическую зависимость между количественными и качественными параметрами рабочего процесса ОР во время переходного режима. При составлении таких уравнений в основу положены законы сохранения энергии (материи) с учетом физических особенностей рабочих процессов, протекающих в объекте. Для пояснения составим уравнение динамики простейшего объекта - бака с уровнем жидкости (рис. 26, а), которая подводится с постоянным напором Н₀ через клапан m и отводится через клапан l .

Рис. 32. Графики устойчивого объекта регулирования

 

Задача регулирования сводится к удержанию уровня жидкости в баке вблизи значения h ₀ путем изменения притока W ₁ при изменении расхода W ₂.

При некотором открытии клапанов наблюдается установившийся режим:

W₁ — W₂ = 0 при h₀ = idem.                               (2)

Например, частичное прикрытие клапана l приведет к уменьшению расхода W ₂. Под действием разности притока и расхода ( W ₁ – W ₂ ) за некоторый промежуток времени Δ t уровень в баке возраст значение Δh. Тогда приращение количества жидкости в баке определится как ( W ₁ — W ₂ )Δ t. Это же приращение можно выразить через изменение уровня Δ h :

где  f — площадь свободной поверхности жидкости;

     р — плотность жидкости;

 W _{1 ,} W ₂ — текущие значения массового секундного притока и расхода.

Разделив полученное равенство на Δ t и вычтя из него почленно уравнение статики, получим уравнение динамики для бака с уровнем жидкости, выраженное в приращениях (3):

где Δ W ₁ = W ₁ - W ₀₁ - изменение соответственно секундного массового притока

Δ W ₂ = W ₂ – W ₀₂ и расхода жидкости.

Правая часть уравнения (Δ W ₁ - Δ W ₂) численно характеризует возмущение, которое в условиях эксплуатации объекта может изменяться произвольно в широких пределах. В левой части уравнения - произведение аккумулирующего коэффициента (fp) на скорость изменения уровня жидкости в баке (Δ h /Δ t).

Аккумулирующий коэффициент характеризует способность объекта накапливать энергию или материю и для рассмотренного случая показывает массу жидкости, приходящуюся на единицу уровня. В зависимости от типа объекта коэффициент может быть постоянным либо меняться при изменении регулируемого параметра. Так, для вертикальной цилиндрической емкости с жидкостью аккумулирующий коэффициент имеет постоянное значение, а для горизонтальной цилиндрической либо конической — переменное. Объясняется это изменением площади поперечного сечения по высоте емкости. Рассмотренный ОР является простым одноемкостным, так как аккумулирует энергию только в одном объеме (емкости).

Скорость изменения уровня жидкости в баке будет тем больше, чем больше возмущение и меньше аккумулирующая способность. А чем больше скорость изменения регулируемого параметра, тем большим быстродействием должен обладать регулятор, установленный на данный объект. Этот вывод справедлив для любого объекта, так как уравнения для различных ОР имеют одинаковые структуру и сущность. Так, для двигателей, имеющих вращающиеся массы (ДВС, турбины и паровые машины), уравнение динамики с точки зрения регулирования частоты вращения вала имеет вид (4):

где       I_ПР — приведенный к валу двигателя момент инерции движущихся масс, характеризующий инерционные свойства двигателя;

         Δω/Δt — изменение угловой скорости вала двигателя, т.е. ускорение;

ΔМ_Д - ΔМ_С — разность приращении крутящего момента двигателя и сопротивления.

Уравнение динамики для емкости с газом с точки зрения регулирования давления при условии, что температура газа остается постоянной при небольших отклонениях давлений, имеет вид:

где  V — объем емкости (величина постоянная);

   R — газовая постоянная;

   υ₀ — температура газа;

 Δp/Δt — скорость изменения давления газа в емкости;

Δ W ₁ - Δ W ₂ — разность приращений притока и расхода газа.

Для объектов, аккумулирующих теплоту, с точки зрения регулирования температуры уравнение динамики примет вид:

ΔQ₁ – ΔО₂- разность приращений подводимой и отводимой теплоты в единицу времени.

Из приведенных уравнений динамики видно, что первый член левой части характеризует аккумулирующую способность ОР, которая у разных объектов может быть различной.

Один и тот же ОР может обладать различным числом аккумулирующих емкостей с различной аккумулирующей способностью. Например, топливная магистраль с паровым топливоподогревателем с точки зрения регулирования давления топлива является простым одноемкостным ОР с малой инерцией. При нанесении возмущения (например, изменении расхода топлива) давление одновременно изменяется во всех точках системы, так как топливо практически несжимаемо. При малом гидравлическом сопротивлении давление в различных точках системы на установившихся режимах одинаковое.

Объект, в котором регулируемый параметр имеет одинаковое значение в различных точках емкости, называется объектом с сосредоточенным параметром.

Эта же система с точки зрения регулирования температуры подогрева топлива является сложным многоемкостным объектом с последовательным включением трех тепловых емкостей, обладающих тепловой инерцией. Инерционность может быть значительной, так как процесс теплообмена протекает довольно медленно с последовательной передачей теплоты от греющего пара к стенкам труб топливоподогревателя, а затем к топливу. В этом случае температура топлива даже при установившемся режиме имеет различные значения в различных точках емкости, возрастая по ходу движения топлива в теплообменнике. Объект, в котором регулируемые параметры на установившихся режимах имеют различные значения по длине емкости, называется объектом с распределенным параметром.

Характер изменения регулируемого параметра объекта регулирования после нанесения возмущения может быть различным в зависимости от числа емкостей, входящих в него, порядка их включения и саморегулирования.

Саморегулирование (самовыравнивание) — способность объекта самостоятельно приходить к установившемуся режиму после вывода его из состояния равновесия.

Саморегулирование характеризует устойчивость ОР, а его значение и знак определяются взаимным расположением статических характеристик подвода и отвода, под которыми понимают статическую зависимость значения притока и расхода энергии (вещества) ОР от значений регулируемого параметра при неизменном состоянии РО и внешних условий.

Так, для бака с уровнем h жидкости (см. рис. 32, а) приток W ₁ (5) и расход W ₂ (6) при определенном открытии клапанов m , l зависит от перепада давлений на них Δ p_m = p ₁ - p ₂ . Δp_l = p ₂ – p ₃. Давление р₂ жидкости у клапанов со стороны бака можно выразить через высоту уровня:

Эти зависимости нелинейны и графически выражаются линиями (рис. 32, б), положение каждой из которых соответствует определенному проходному сечению клапанов. Если клапаны открыты на некоторое фиксированное значение, то установившийся режим графически определится точкой А пересечения характеристик подвода m ₁ и отвода l ₁ , т. е. W ₀ = W ₀₁ = W ₀₂ при h₀₁ = idem.

Например, частичное прикрытие клапана l приводит к смещению характеристики отвода в положение l_г . Тогда в начальный момент при прежнем уровне h ₀₁ расход уменьшается до значения W ´₂ , а приток остается прежним W_a. Под действием разности (W ₀ - W ₂) уровень воды в баке начинает расти. Однако чем выше уровень, тем меньше становится разница между притоком и расходом. И, наконец, в точке В пересечения характеристики т₁ притока с характеристикой l₂ отвода наступает установившийся режим: W ´₀ = W ´₀₁ = W ´₀₂ при h₀₂ = idem.

Таким образом, объект после нанесения возмущения самостоятельно пришел к новому установившемуся режиму при новых значениях параметров. Причем по мере изменения уровня первоначальное возмущение (W ₀₁ – W ´₂) уменьшалось, стремясь к нулю, а из уравнения динамики объекта (3) следует, что если возмущение стремится к нулю, то и скорость изменения уровня Δh / Δt также будет стремиться к нулю.

В том случае, если после вывода ОР из равновесного состояния скорость изменения регулируемого параметра стремится к нулю, а сам параметр - к конечному значению, принято считать такое саморегулирование положительным, а объект устойчивым.

Изменение регулируемого параметра во времени под действием ступенчатого возмущения при неизменном положении РО графически описывается разгонной характеристикой ОР.

Разгон устойчивого одноемкостного объекта осуществляется по экспоненте 1 (рис. 33, а). При этом сразу после нанесения возмущения регулируемый параметр х изменяется с максимальной скоростью, которая к концу переходного процесса t ₁ стремится к нулю.

Рис. 33. Разгонные характеристики объектов регулирования.

 

Если в рассмотренном объекте приток W ₁ и расход W ₂ зависят от уровня h жидкости в баке, то, например, в паровом котле с установившимся давлением пара р_к уровень h воды в барабане не влияет на приток питательной воды D _П.В. расход пара D _П. Объясняется это тем, что напор, создаваемый питательным насосом, превышает напор от давления пара р_к и во много раз превышает напор от изменения уровня воды Δ h в пароводяном барабане. Тогда приток воды D _П (рис. 34, а) зависит только от открытия питательного клапана, что соответствует характеристике притока т₁ . Аналогичное расположение имеет характеристика l ₁ расхода пара D _П из котла. В этом случае характеристики подвода и отвода расположены параллельно и значение нанесенного возмущения остается постоянным при любом уровне h. Тогда, как следует из уравнения динамики (3), уровень будет изменяться с постоянной скоростью.

В том случае, если после вывода ОР из равновесного состояния регулируемый параметр изменяется с постоянной скоростью, принято считать саморегулирование нулевым, а объект нейтральный. Статические характеристики подвода и отвода энергии таких объектов располагаются параллельно, а регулируемый параметр может принимать любые установившиеся значения при условии совмещения характеристик.

Разгонная характеристика одноемкостного нейтрального объекта представляет собой прямую линию 2 (см. рис. 33, а), наклон которой зависит от скорости изменения регулируемого параметра. В действительности у парового котла из-за явления «набухания уровня» разгонная характеристика имеет несколько иной вид.

Рис. 34. Статические характеристики объектов регулирования.

 

Иными свойствами обладает ДГ переменного тока, в электрической цепи которого установлен быстродействующий регулятор напряжения. Характеристикой подвода энергии является характеристика 1 дизеля (рис. 34, б) при фиксированном положении органов управления топливоподачи. Вид и положение этой характеристики определяются свойствами самого дизеля, организацией его рабочего процесса, системой наддува, свойствами и настройкой топливной аппаратуры. Характеристикой отвода энергии дизеля является генераторная характеристика 2, положение и вид которой определяются свойствами генератора, системы его возбуждения и нагрузкой. Установившийся режим графически определяется параметрами точки А пересечения этих характеристик:

 

Например, при отключении части потребителей энергии нагрузка уменьшается до значения М´_С2 и генераторная характеристика смещается в положение 2´. Под действием разности моментов (M ₀₁ - М´_С2) возрастает частота вращения n вала ДГ; чем выше ее значение, тем больше становится возмущение. Так, при частоте вращения n ₂ разность моментов, достигает значения М_Д2 — М_С2, причем (М_Д2-М_С2)>( M ₀₁ - М´_С2). Это приводит к дальнейшему росту частоты вращения и разности моментов, а как следует из уравнения динамики объекта, угловая скорость вала возрастает с ускорением Δω / Δt .

В том случае, если после вывода ОР из равновесия регулируемый параметр изменяется с нарастающей скоростью, принято считать саморегулирование отрицательным, а объект неустойчивым.

Разгонная характеристика 3 (см. рис 33, а) неустойчивого одноемкостного ОР показывает, что регулируемый параметр х изменяется с нарастающей скоростью и при отсутствии регулятора может достичь недопустимых значений.

Если в рассмотренном примере приводным двигателем генератора является паровая турбина (характеристика 3 подвода располагается круче характеристики 2 отвода), то ОР будет устойчивым (см. рис. 34, б).

Чем больше устойчивость ОР, тем более устойчива будет вся АСР. Количественная оценка устойчивости ОР определяется фактором устойчивости F_y либо коэффициентом саморегулирования z. Выяснить физическую сущность этих величин можно, например, преобразовав правую часть уравнения с учетом факторов, влияющих на значения ΔW ₁ и ΔW ₂ (рис. 32, в). Для бака с уровнем жидкости при условии постоянных значений p ₁ ,р₃, К_m и К _l из уравнений (5) и (6) следует, что изменение притока Δ W ₁ и расхода Δ W ₂ зависит от изменения открытия клапанов m и l и уровня h воды в баке:

Тогда при условии достаточно малых статических приращений уровня Δ h ₀ и открытий клапанов Δ m ₀, Δ l ₀ изменение притока можно выразить зависимостями (7), (8):

 

 

Полученные зависимости линейны, поэтому действительные характеристики клапанов т и l (см. рис. 32, б) заменим отрезками касательные проведенных к ним в точке А (см. рис. 32, в). Такая замена нелинейных функций линейными называется линеаризацией и приемлема при малых отклонениях параметров в исследуемой зоне, позволяет упростить решение дифференциальных уравнений. Этот метод тем точнее описывает процесс, чем меньше кривизна характеристик. После подстановки выражений (7) и (8) в уравнение (3), группировки членов и перехода к бесконечно малым приращениям получим:

или, перенеся в левую часть уравнения члены, включающие отклонения регулируемого параметра, получим уравнение (9):

                             (9)

Фактор устойчивости характеризуется знаком и установившимся значением разности отвода и подвода ОР, отнесенным к единице приращения регулируемого параметра. В рассмотренном примере Δ W ₀— это разность изменения величин отвода Δ W ₀₂ и подвода Δ W ₀₁ от повышения уровня Δ h ₀, а направлена она в сторону снижения уровня и восстановления нарушенного равновесия, т.е. F_y имеет положительное значение. Следовательно, при F_y > 0 обьект устойчив, F_y < 0 — объект неустойчив, F_y = 0 — обьект нейтрален.

Уравнение динамики OP (9), выраженное в приращениях, можно привести к безразмерному виду. Для этого произведем следующие действия:

обе части уравнения разделим на номинальное значение нагрузки W _Н; левую часть умножим и разделим на номинальное значение уровня h _Н;

первое слагаемое правой части уравнения умножим и разделим на номинальное открытие клапана m_Н;

второе слагаемое правой части уравнения умножим и разделим на номинальное значение открытия клапана l_Н.

В результате получим:

(10)

 

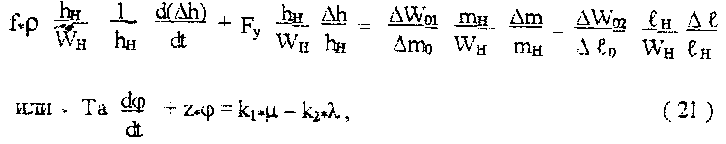
Уравнение динамики любого одноемкостного объекта может быть приведено к общему виду (10). В правой части уравнения — возмущение, выраженное в относительных (безразмерных) единицах подвода. Для ОР, в которых отсутствует процесс преобразования энергии, коэффициенты k ₁ и k _г характеризуют пропорциональность расходных статических характеристик подвода и отвода. Так, в рассмотренном примере k ₁ и k _г характеризуют расходные характеристики клапанов соответственно m и l. Левая часть уравнения соответствует возмущению ОР, выраженному через относительное изменение регулируемого параметра.

Из уравнения следует, что при нанесении ступенчатого возмущения изменяется регулируемый параметр, а характер этого изменения определяется знаком коэффициента саморегулирования z, однозначно определяемым знаком фактора устойчивости F_y. Чем больше наносимое возмущение и меньше время Т_а объекта, тем выше скорость изменения регулируемого параметра в момент нанесения возмущения.

Время объекта - это время, в течение которого энергия накопленная объектом, может быть полностью использована (с номинальным расходом) при условии изменения регулируемого параметра от номинального значения до нулевого с постоянной скоростью. Мерой инерционности устойчивых одноемкостных объектов (z > 0) является также постоянная времени разгона Т объекта, значение которой определяется не только инерционностью объекта, но и саморегулированием: Т = Т_а / z.

Для одного и того же ОР значения коэффициента саморегулирования z могут быть различны в зависимости от взаимного расположения характеристик подвода и отвода в исследуемой зоне, а следовательно, различные значения будет принимать постоянная времени разгона Т объекта. При наличии разгонной характеристики Т объекта (см. рис. 33, б) может быть определено графически. Для этого к разгонной характеристике 1 в любой точке проводят касательную до пересечения с линией установившегося значения параметра φ ₀₁. Тогда проекция отрезка касательной, заключенного между этими точками, на ось времени в масштабе определит постоянную времени разгона Т объекта. Таким образом, эта величина является временем экспоненты разгона объекта. Значение Т можно также определить из уравнения (10) как время, в течение которого регулируемый параметр достигает значения φ ₁ = 0,63 φ ₀₁ с момента нанесения скачкообразного возмущения любого значения со стороны подвода либо отвода энергии объекта.

Уравнение динамики одноемкостного устойчивого объекта может быть представлено в иной форме, если все члены уравнения (10) разделить на коэффициент саморегулирования z:

(11)

Коэффициенты усиления k_μ и k_λ характеризуются статическими свойствами объекта в точках исходных установившихся режимов и могут быть определены практически из уравнения (11) при условии dφ / dt =0.

Для определения k_μ необходимо, не меняя нагрузки (λ =0), изменить подвод энергии объекта, измерив значение μ₀ и определить соответствующее изменение регулируемого параметра φ₀. Тогда k_μ = φ ₀ / μ ₀.

Значение k_λ определяют аналогично при μ=0 из соотношения k_λ =φ₀/λ_0.

Большинство ОР с распределенными параметрами являются сложными многоемкостными, в которых энергия (материя) распределена по нескольким аккумулирующим емкостям. Если аккумулирующие емкости располагаются последовательно, то наблюдается некоторая задержка изменения регулируемого параметра х по времени с момента t ₀ нанесения возмущения (характеристика 4 на рис 33, а). Отрезок времени τ₀ с момента нанесения ступенчатого возмущения до начала изменения регулируемого параметра называется чистым, передаточным или транспортным запаздыванием объекта.

Примером сложного объекта с распределенным параметром, последовательным соединением емкостей и сопротивлением между ними является система охлаждения дизеля, температура воды в которой на установившемся режиме различна, т.е. распределена по длине объекта. В контуре пресной воды с момента изменения нагрузки дизеля до момента изменения температуры воды на входе в холодильник проходит некоторый промежуток времени. Это время перемещения волны теплового потока в контуре двигателя и трубопровода до холодильника является чистым запаздыванием. Очевидно, чем больше тепловое сопротивление металла двигателя, длина трубопровода и меньше скорость потока воды, тем больше значение τ₀ .

Следовательно, значение чистого запаздывания τ₀  зависит от скорости движения волны измененного параметра по емкостям и длины связей между ними. Чистое запаздывание может отсутствовать у многоемкостных ОР и наблюдаться у одноемкостных.

В объекте регулирования с последовательным включением емкостей регулируемый параметр вначале изменяется с нарастающей скоростью (до точки А, см. рис. 33, а), а затем с убывающей. Касательная, проведенная через точку А перегиба разгонной характеристики, отсекает по оси времени величину τ_П, называемую переходным запаздыванием. Переходное запаздывание объясняется наличием в ОР нескольких последовательно соединенных емкостей, в каждой из которых происходит свой переходный процесс. Так, в системе охлаждения вначале теплота передается от массы газов к массе металла двигателя, а затем к массе охлаждающей воды. Чем больше число последовательно соединенных емкостей, аккумулирующая способность каждой и сопротивление между ними, тем больше переходное запаздывание ОР.

Сумма чистого и переходного запаздывания определяет полное запаздывание объекта:  τ = τ _о + τ _п.

Качественное регулирование процесса и динамическую устойчивость АСР обеспечить тем труднее, чем больше значение отношения запаздывания к постоянной времени разгона объекта τ / Т.

Таким образом, инерционность, саморегулирование и запаздывание объекта в значительной степени влияют на динамику процесса регулирования. Эти факторы следует учитывать при выборе и настройке регуляторов. Несоответствие типа регулятора или его настройки свойствам ОР может привести к неустойчивому переходному процессу с недопустимым динамическим забросом регулируемого параметра и большим временем переходного процесса.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться: