|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Решения задач 1.1 – 1.3 диагностической работыСтр 1 из 3Следующая ⇒
Диагностическая работа
1.1. В единичном кубе A…D1 найдите угол между прямыми AB1 и BC1.
1.2. В единичном кубе A…D1 найдите угол между прямыми DA1 и BD1.
1.3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 – соответственно середины ребер A1C1 и B1C1.
2.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой AF и плоскостью BCC1.
2.2. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой CC1 и плоскостью BDE1.
2.3. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD, где E – середина ребра SC.
3.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между плоскостями AFF1 и DEE1.
3.2. В единичном кубе A…D1 найдите тангенс угла между плоскостями
ADD1 и BDC1.
3.3. В правильной треугольной призме ABCA1B1C1D1, все ребра которой равны 1, найдите косинус угла между плоскостями ACB1 и BA1C1.
4.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до прямой D1F1.
4.2. В единичном кубе A…D1 найдите расстояние от точки A до прямой BD1.
4.3. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки F до прямой BG, где G – середина ребра SC.
5.1. В единичном кубе A…D1 найдите расстояние от точки A до плоскости BDA1.
5.2. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SBC.
5.3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BFE1.
6.1. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC.
6.2. В единичном кубе A…D1 найдите расстояние между прямыми AB1 и BC1.
6.3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми AA1 и CF1.
Тренировочная работа 5. Расстояние от точки до плоскости
В единичном кубе A…D1 найдите расстояние от точки A до плоскости CB1D1.
2.
В единичном кубе A…D1 найдите расстояние от точки A до плоскости BDC1.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BCA1.
4. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки A до плоскости CA1B1.
5. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SCD.
6. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SDE.
7. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости DEA1.
8. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости DEF1.
Диагностическая работа 1
1. В кубе A…D1 найдите угол между прямыми BA1 и B1D1.
2. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и DC1.
4. В кубе A…D1 найдите синус угла между прямой A1D1 и плоскостью ACB1.
5. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой AB и плоскостью SBC.
6. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите синус угла между прямой AF1 и плоскостью BCC1.
7. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями
ABC и SCD.
8. В правильной шестиугольной призме A…F1 найдите угол между плоскостями AFF1 и BCC1.
9. В кубе A…D1 найдите косинус угла между плоскостями
AB1D1 и CB1D1.
10. В единичном кубе A…D1 найдите расстояние от точки B до прямой DA1.
11. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до прямой EB1.
12. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до прямой SD.
13. В единичном кубе A…D1 найдите расстояние от точки B до плоскости DA1C1.
14. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BFA1.
15. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SCE.
16. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние между прямыми AA1 и BC.
17. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми BB1 и CD1.
18. В единичном кубе A…D1 найдите расстояние между прямыми AB1 и BD1.
1. В кубе A…D1 найдите угол между прямыми AB1 и BD1.
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка E – середина ребра SB. Найдите тангенс угла между прямыми SA и BE.
3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1.
4. В кубе A…D1 найдите синус угла между прямой DD1 и плоскостью ACB1.
5. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой AF и плоскостью SBC.
6. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите синус угла между прямой BC1 и плоскостью BCE1.
7. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями ABC и SEF.
8. В правильной шестиугольной призме A…F1 найдите угол между плоскостями AFF1 и BDD1.
9. В кубе A…D1 найдите тангенс угла между плоскостями
ABC и DA1C1.
10. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки A до прямой CB1.
11. В правильной шестиугольной призме A … F1, все ребра которой равны 1, найдите расстояние от точки A до прямой BE1.
12. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до прямой SC.
13. В единичном кубе A…D1 найдите расстояние от точки B до плоскости AB1D1.
14. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости CEF1.
15. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SBF.
16. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние между прямыми AA1 и BC1.
17. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми BB1 и FE1.
18. В единичном кубе A…D1 найдите расстояние между прямыми BA1 и B1D1.
Диагностическая работа 3 1. В правильном тетраэдре ABCD найдите угол между прямыми AB и CD.
2. В кубе A…D1 найдите тангенс угла между прямыми AB и DB1.
3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите косинус угла между прямыми BA1 и DB1. 4. В кубе A…D1 найдите угол между прямой AС и плоскостью BCD1.
5. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой SA и плоскостью SBC.
6. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите синус угла между прямой FC1 и плоскостью BCE1.
7. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка E – середина ребра SC. Найдите угол между плоскостями ABC и BDE.
8. В кубе A…D1 найдите угол между плоскостями ABC1 и BCD1.
9. В правильной шестиугольной призме A … F1, все ребра которой равны 1, найдите угол между плоскостями ABC и BFE1.
10. В единичном кубе A…D1 найдите расстояние от точки B до прямой AC1.
11. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до прямой SB.
12. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до прямой CF1.
13. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка E – середина ребра SB. Найдите расстояние от точки B до плоскости ACE.
14. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки B до плоскости AB1C1.
15. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости CFA1.
16. В единичном кубе A…D1 найдите расстояние между прямыми AB и CA1.
17. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние между прямыми SB и DF.
18. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми BB1 и CF1.
Ответы Тренировочная работа 1 1. Тренировочная работа 2 1. Тренировочная работа 3 1. Тренировочная работа 4 1. Тренировочная работа 5 1. Тренировочная работа 6 1.
Диагностическая работа 1 1. 60о. 2. Диагностическая работа 2 1. 90о. 2. Диагностическая работа 3 1. 90о. 2. Содержание От редакторов серии ……………………………………………
Введение ……………………………………………
Диагностическая работа ……………………………………………
Решения задач 1.1 – 1.3 диагностической работы …………………
Тренировочная работа 1 ……………………………………………
Решения задач 2.1 – 2.3 диагностической работы ………………
Тренировочная работа 2 ……………………………………………
Решения задач 3.1 – 3.3 диагностической работы………………
Тренировочная работа 3……………………………………………
Решения задач 4.1 – 4.3 диагностической работы………………
Тренировочная работа 4……………………………………………
Решения задач 5.1 – 5.3 диагностической работы……………
Тренировочная работа 5……………………………………………
Решения задач 6.1 – 6.3 диагностической работы……………
Тренировочная работа 6……………………………………………
Диагностическая работа 1……………………………………………
Диагностическая работа 2……………………………………………
Диагностическая работа 3……………………………………………
Ответы……………………………………………
Диагностическая работа
1.1. В единичном кубе A…D1 найдите угол между прямыми AB1 и BC1.
1.2. В единичном кубе A…D1 найдите угол между прямыми DA1 и BD1.
1.3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 – соответственно середины ребер A1C1 и B1C1.
2.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой AF и плоскостью BCC1.
2.2. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой CC1 и плоскостью BDE1.
2.3. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD, где E – середина ребра SC.
3.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между плоскостями AFF1 и DEE1.
3.2. В единичном кубе A…D1 найдите тангенс угла между плоскостями
ADD1 и BDC1.
3.3. В правильной треугольной призме ABCA1B1C1D1, все ребра которой равны 1, найдите косинус угла между плоскостями ACB1 и BA1C1.
4.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до прямой D1F1.
4.2. В единичном кубе A…D1 найдите расстояние от точки A до прямой BD1.
4.3. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки F до прямой BG, где G – середина ребра SC.
5.1. В единичном кубе A…D1 найдите расстояние от точки A до плоскости BDA1.
5.2. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SBC.
5.3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BFE1.
6.1. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC.
6.2. В единичном кубе A…D1 найдите расстояние между прямыми AB1 и BC1.
6.3. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми AA1 и CF1.
Решения задач 1.1 – 1.3 диагностической работы
1.1. Первое решение. Прямая AD1 параллельна прямой BC1 и, следовательно, угол между прямыми AB1 и BC1 равен углу B1AD1. Треугольник B1AD1 равносторонний и, значит, угол B1AD1 равен 60о.
Второе решение. Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1. Вектор
Ответ. 60о.
1.2. Первое решение. Рассмотрим ортогональную проекцию AD1 прямой BD1 на плоскость ADD1. Прямые AD1 и DA1 перпендикулярны. Из теоремы о трех перпендикулярах следует, что прямые DA1 и BD1 также перпендикулярны, т.е. искомый угол между прямыми DA1 и BD1 равен 90о.
Второе решение. Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1. Вектор 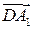 имеет координаты (0, -1, 1). Вектор  имеет координаты (-1, 1, 1). Скалярное произведение этих векторов равно нулю и, значит, искомый угол между прямыми DA1 и BD1 равен 90о.
Ответ. 90о.
1.3. Первое решение. Обозначим D и F1 соответственно середины ребер AC и A1B1.
Прямые DC1 и DF1 будут соответственно параллельны прямым AD1 и CE1. Следовательно, угол между прямыми AD1 и CE1 будет равен углу C1DF1. Треугольник C1DF1 равнобедренный, DC1 = DF1 = Второе решение. Введем систему координат, считая началом координат точку A, как показано на рисунке. Точка C имеет координаты
Ответ. 0, 7.
|
Последнее изменение этой страницы: 2019-04-09; Просмотров: 550; Нарушение авторского права страницы
. 2. 
. 3. 
. 4. 
. 5. 
. 7. 
. 8. 
.
. 2. 
. 3. 
. 4. 
. 5. 
. 6. 
. 7. 60. 8. 
.
. 3. 
. 4. 
. 6. 0, 6. 7. 0, 2. 8. 
.
. 2. 
. 3. 
. 4. 
. 5. 
. 6. 
. 8. 
. 
. 4. 
. 6. 
. 7. 
.
. 2. 
. 8. 
. 6. 
. 7. 
. 11. 
. 12. 
. 13. 
. 15. 
. 16. 
. 
. 7. 
. 11. 
. 12. 
. 13. 
. 15. 
. 16. 
. 4. 30о. 5. 
. 6. 
. 16. 
. 17. 
. 18. 
имеет координаты (1, 0, 1). Вектор 
имеет координаты (0, 1, 1). Воспользуемся формулой нахождения косинуса угла 
между векторами 
и, значит, угол 
, C1F1 = 
. Используя теорему косинусов, получаем 
.
, точка D1 имеет координаты 
, точка E1 имеет координаты 
. Вектор 
имеет координаты 
. Вектор 
имеет координаты 
. Косинус угла между прямыми AD1 и CE1 равен косинусу угла между векторами 
между векторами. Получим 
.