Решения задач 5.1 – 5.3 диагностической работы

5.1. Первое решение. Пусть O – середина отрезка BD. Прямая BD перпендикулярна плоскости AOA₁. Следовательно, плоскости BDA₁ и AOA₁ перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA₁, является высота AH прямоугольного треугольника AOA₁, в котором AA₁ = 1, AO = , OA₁ = . Для площади S этого треугольника имеют место равенства . Откуда находим AH = .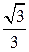

Второе решение. Пусть O – середина отрезка BD. Прямая BD перпендикулярна плоскости AOA₁. Следовательно, плоскости BDA₁ и AOA₁ перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA₁, является высота AH прямоугольного треугольника AOA₁, в котором AA₁ = 1, AO = , OA₁ = . Треугольники AOA₁ и HOA подобны по трем углам. Следовательно, AA₁: OA₁ = AH: AO. Откуда находим AH = .

Третье решение. Пусть O – середина отрезка BD. Прямая BD перпендикулярна плоскости AOA₁. Следовательно, плоскости BDA₁ и AOA₁ перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA₁, является высота AH прямоугольного треугольника AOA₁, в котором AA₁ = 1, AO = , OA₁ = . Откуда  и, следовательно,

Ответ. .

 

5.2. Первое решение. Пусть O – центр основания пирамиды. Прямая AO параллельна прямой BC и, значит, параллельна плоскости SBC. Следовательно, искомое расстояние равно расстоянию от точки O до плоскости SBC. Пусть G – середина отрезка BC. Тогда прямая OG перпендикулярна BC и искомым перпендикуляром, опущенным из точки O на плоскость SBC, является высота OH прямоугольного треугольника SOG. В этом треугольнике OG = , SG = , SO = 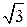. Для площади S этого треугольника имеют место равенства . Откуда находим OH = .

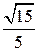Второе решение. Пусть O – центр основания пирамиды. Прямая AO параллельна прямой BC и, значит, параллельна плоскости SBC. Следовательно, искомое расстояние равно расстоянию от точки O до плоскости SBC. Пусть G – середина отрезка BC. Тогда прямая OG перпендикулярна BC и искомым перпендикуляром, опущенным из точки O на плоскость SBC, является высота OH прямоугольного треугольника SOG. В этом треугольнике OG = , SG = , SO = . Треугольники SOG и OHG подобны по трем углам. Следовательно, SO: SG = OH: OG. Откуда находим OH = .

Ответ. .

5.3. Первое решение. Пусть O и O₁ – центры оснований призмы. Прямая AO₁ параллельна плоскости BFE₁ и, следовательно, расстояние от точки A до плоскости BFE₁ равно расстоянию от прямой AO₁ до плоскости BFE₁. Плоскость AOO₁ перпендикулярна плоскости BFE₁ и, следовательно, расстояние от прямой AO₁ до плоскости BFE₁ равно расстоянию от прямой AO₁ до линии пересечения GG₁ плоскостей AOO₁ и BFE₁. Треугольник AOO₁ прямоугольный, AO = OO₁ = 1, GG₁ – его средняя линия. Следовательно, расстояние между прямыми AO₁ и GG₁ равно половине высоты OH треугольника AOO₁, т.е. равно .

Второе решение. Пусть G – точка пересечения прямых AD и BF. Угол между прямой AD и плоскостью BFE₁ равен углу между прямыми BC и BC₁ и равен 45^о. Перпендикуляр AH, опущенный из точки A на плоскость BFE₁, равен . Так как AG = 0, 5, то AH = .

Ответ. .

⇐ Предыдущая123Следующая ⇒

Поделиться: