НЕЯВНІ ФУНКЦІЇ ТА ЇХ ДИФЕРЕНЦІЮВАННЯ
Розглянемо рівняння
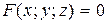
| (8)
|
Якщо для всіх (x; y) з деякої множини  існує така функція (не обов'язково єдина), при підстановці якої в (8) ця рівність виконується тотожно в D, то говорять, що рівняння (8) визначає на множині D неявну функцію
існує така функція (не обов'язково єдина), при підстановці якої в (8) ця рівність виконується тотожно в D, то говорять, що рівняння (8) визначає на множині D неявну функцію 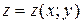 .
.
Приклад 10. Рівняння  визначає неявно дві неперервні функції
визначає неявно дві неперервні функції 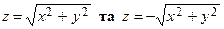 (або одну двозначну функцію
(або одну двозначну функцію 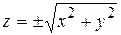 ) з областями визначення кожної
) з областями визначення кожної  .
.
Проте отримати явну залежність  з рівняння вигляду (8) не завжди можливо, до того ж воно може і не визначати ніякої функції. Тому вельми важливо знать умови, які б гарантували існування такої неявно заданої функції
з рівняння вигляду (8) не завжди можливо, до того ж воно може і не визначати ніякої функції. Тому вельми важливо знать умови, які б гарантували існування такої неявно заданої функції  .
.
ТЕОРЕМА. Про існування неявної функції.
Нехай координати точки 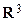 задовольняють рівнянню (8), причому функція
задовольняють рівнянню (8), причому функція 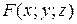 та її частинні похідні
та її частинні похідні  ,
, 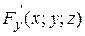 ,
,  , неперервні в околі точки
, неперервні в околі точки 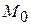 , та
, та  . Тоді існує такий окіл точки
. Тоді існує такий окіл точки  , в якій визначена єдина функція, що неперервно диференціюється, та задовольняє рівняння (8), така, що точка
, в якій визначена єдина функція, що неперервно диференціюється, та задовольняє рівняння (8), така, що точка 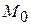 є точкою її графіка.
є точкою її графіка.
Помітимо, що теорема не вказує методу знаходження цієї неявної функції, а тільки стверджує, що така функція існує. Проте виявляється, що частинні похідні  і
і  цієї невідомої функції можуть бути обчислені.
цієї невідомої функції можуть бути обчислені.
Нехай умови теореми виконані, й  – неявна функція. Підставляючи її в рівняння (8), отримаємо тотожність, справедливу при всіх (x; у) з деякого околу точки
– неявна функція. Підставляючи її в рівняння (8), отримаємо тотожність, справедливу при всіх (x; у) з деякого околу точки  . Продиференціюємо обидва частини цієї тотожності по змінні x, використовуючи правило диференціювання складної функції.
. Продиференціюємо обидва частини цієї тотожності по змінні x, використовуючи правило диференціювання складної функції.
  . .
|
(9)
|
Аналогійно визначається і частинна похідна  :
:
  . .
|
(10)
|
Зауваження. У разі, коли рівняння  неявно визначає функцію однієї змінної, що диференціюється, можна, діючи аналогійно, обчислити звичайну похідну
неявно визначає функцію однієї змінної, що диференціюється, можна, діючи аналогійно, обчислити звичайну похідну  , якщо
, якщо 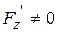 .
.
ДОТИЧНА ПЛОЩИНА ДО ПОВЕРХНІ І ГЕОМЕТРИЧНЕ ЗНАЧЕННЯ ДИФЕРЕНЦІАЛА
 Геометричне зміст диференціала функції двох змінних
Геометричне зміст диференціала функції двох змінних  пов'язано з дотичною площиною до поверхні, яка визначаєтьсяною цією функцією.
пов'язано з дотичною площиною до поверхні, яка визначаєтьсяною цією функцією.
Нехай  функція, що диференціюється в околі точки
функція, що диференціюється в околі точки  , а поверхня S – її графік. Розглянемо перетин поверхні площиною
, а поверхня S – її графік. Розглянемо перетин поверхні площиною 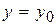 і проведемо дотичну пряму в точки
і проведемо дотичну пряму в точки  до лінії перетину. Аналогійним чином побудуємо дотичну до лінії перетину площиною
до лінії перетину. Аналогійним чином побудуємо дотичну до лінії перетину площиною 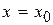 (мал.3).
(мал.3).
Площина, що проходить через ці дві дотичні, які перетинаються, називається дотичною площиною до поверхні  в точці
в точці  . Її рівняння
. Її рівняння
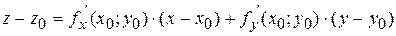
| (11)
|
де  .
.
Можна показати, що для будь-якої лінії на поверхні, що проходить через точку  , дотична пряма, проведена до лінії через цю точку, лежить в дотичній площині.
, дотична пряма, проведена до лінії через цю точку, лежить в дотичній площині.
НОРМАЛЬ ДО ПОВЕРХНІ
Вектор  , який перпендикулярен дотичній площини, називається нормальним вектором до поверхні, а пряма, перпендикулярна до дотичної площини, що проходить через точку дотику, називається нормаллю до поверхні в даній точці.
, який перпендикулярен дотичній площини, називається нормальним вектором до поверхні, а пряма, перпендикулярна до дотичної площини, що проходить через точку дотику, називається нормаллю до поверхні в даній точці.
З рівняння (11) вектор  є нормальним до поверхні
є нормальним до поверхні  (причому будь-який вектор, пропорційний йому,
(причому будь-який вектор, пропорційний йому, 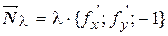 – теж нормальний). Звідси випливає, що рівняння нормалі до поверхні в точці
– теж нормальний). Звідси випливає, що рівняння нормалі до поверхні в точці  має вигляд
має вигляд

Нехай тепер поверхня S задана неявним рівнянням 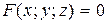 , яке визначає в околі точки
, яке визначає в околі точки  диференціьовану функцію
диференціьовану функцію  , причому
, причому  . Згідно правил диференціювання неявної функції (9)-(10) (якщо
. Згідно правил диференціювання неявної функції (9)-(10) (якщо  )
)
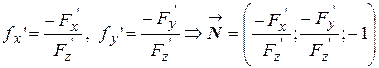 .
.
Для зручності помножимо  на множник
на множник  , отримаємо інший нормальний вектор
, отримаємо інший нормальний вектор  , де всі похідні обчислюються в точці
, де всі похідні обчислюються в точці  . Таким чином, приходимо в цьому випадку до рівняння нормалі
. Таким чином, приходимо в цьому випадку до рівняння нормалі
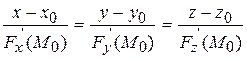
| (12)
|
Відмітимо, що рівняння дотичної площини можна записати у вигляді
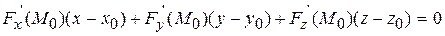
| (13)
|
Хоча раніше було зроблено припущення, що 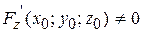 , але рівняння (12), (13) справедливі і коли
, але рівняння (12), (13) справедливі і коли  . Вони не мають сенсу тільки в тому випадку, якщо все три частинні похідні дорівнюють нулю одночасно.
. Вони не мають сенсу тільки в тому випадку, якщо все три частинні похідні дорівнюють нулю одночасно.
Точка  називається особливою точкою поверхні
називається особливою точкою поверхні  , якщо
, якщо 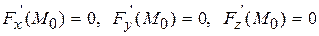 .
.
В особливій точці дотична площина і нормаль до поверхні не визначені.
Приклад 11: Знайти рівняння дотичної площини і нормалі до конуса  (мал.4) в точках
(мал.4) в точках  та
та  .
.
 Розв'язок:
Розв'язок:  .
.
 , значить, в точці M нормальний вектор
, значить, в точці M нормальний вектор  , рівняння дотичної площини за формулою (13) має вигляд
, рівняння дотичної площини за формулою (13) має вигляд

або після розкриття дужок і скорочення на 4
 ,
,
а рівняння нормалі за формулою (12) –
 .
.
В точці  ,
,  значить, це особлива точка поверхні, і в ній дотична площина і нормаль не визначені.
значить, це особлива точка поверхні, і в ній дотична площина і нормаль не визначені.

