НАЙБІЛЬШЕ І НАЙМЕНШЕ ЗНАЧЕННЯ ФУНКЦІЇ В ЗАМКНУТІЙ ОБМЕЖЕНІЙ ОБЛАСТІ

Розглянемо декілька визначень.

Точка P називається внутрішньою точкою множини 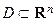, якщо вона належить D разом з деяким свїм околом.

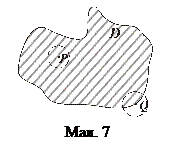
Точка Q називається граничною точкою множини D, якщо в будь-якому її околі є як точки, що належать множині D, так і точки, що не належать цій множині (мал.7). Сукупність всіх граничних точок множини D називається його межею.

 

Множина 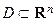називається відкритою областю (або просто областю), якщо всі її точки внутрішні і будь-які дві з них можна з'єднати лінією, всі точки якої належать множині D. Якщо до області D приєднати її межу, то отримана множина точок називається замкнутою областю і позначається .

 

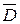Область називається обмеженою, якщо вона повністю лежить у середині деякого околу початку координат.

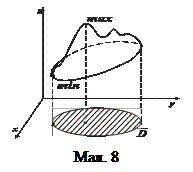 ТЕОРЕМА. Неперервна функція двох змінних в замкнутій обмеженій області  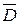досягає своїх найбільшого і найменшого значень або у середині області в точках екстремуму, або на її межі (мал. 8).

Висновок. Щоб знайти найбільше або найменше значення функції двох змінних, що диференціюється, в замкнутій обмеженій області 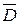 треба:

1. Знайти всі стаціонарні (підозрілі на екстремум) точки у середині області і обчислити в них значення функції.

2. Знайти найбільше або відповідно найменше значення функції на межі області, тобто знайти умовний екстремум функції одним з вищевикладених методів.

3. Порівняти ці значення і вибрати з них потрібне.

Приклад 13. Знайти найбільше і найменше значення функції 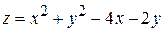 в замкнутій області 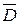, обмеженій лініями 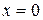,  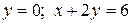(мал.9).

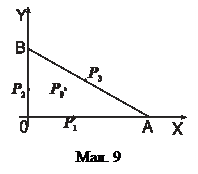Розв'язок. а) Знайдемо всі стаціонарні точки функції у середині області :

.

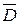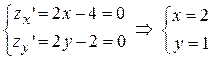Отже, усередині області 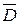 є єдина стаціонарна точка  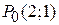і функція приймає в ній значення .

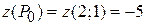б) Розіб'ємо межу 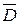 на три відрізки OA, OB і AB. На кожному з них нам необхідно вирішити задачу знаходження умовного екстремуму, для чого ми скористаємося першим з викладених вище методів, виключаючи за допомогою рівняння зв'язку одну із змінних. Проте повністю вирішувати ці задачі ми не будемо, а знайдемо тільки точки підозрілі на екстремум.

На ділянці OA: 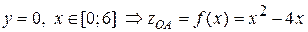. Ця функція неперервно диференціюється і може досягати своїх найбільшого і найменшого значень або у середині відрізка в стаціонарній точц, або на його кінцях. Стаціонарні точки знаходимо з рівняння 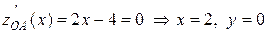. Функція в цій точпці  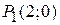приймає значення 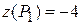. Обчислимо також значення функції на кінцях відрізка в крапках О(0; 0) і А(0; 6): .

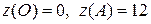На ділянці OB: 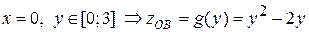. Критичну точку знаходимо з рівняння 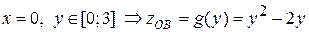. Функція приймає в цій точці  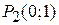значення 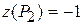. Обчислюємо значення функції в точці B: .

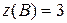На ділянці AB: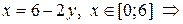

.

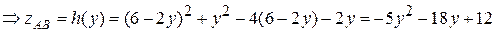Прирівнюючи до нуля похідну цій функції 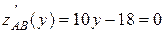, одержуємо координати її критичної точки: 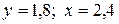. Функція приймає в цій точцці  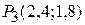значення .

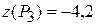Порівнюючи значення функції в точках 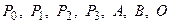, знаходимо, що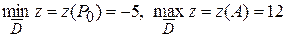

ІНДИВІДУАЛЬНІ ЗАВДАННЯ

ЗАВДАННЯ 1  Обчислити 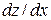, використовуючи правило диференціювання складної функції, якщо .

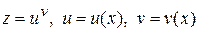1.

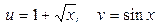
2.

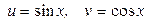
3.

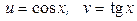
4.

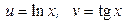
5.

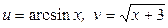
6.

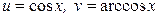
7.

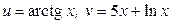
8.

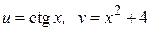
9.

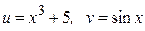
10.

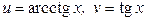
11.

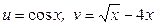
12.

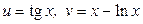
13.

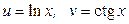
14.

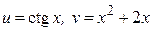
15.

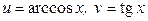
16.

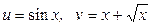
17.

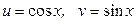
18.

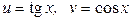
19.

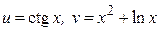
20.

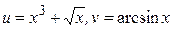
21.

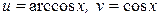
22.

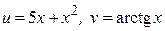
23.

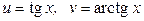
24.

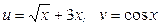
25.

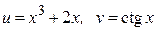
26.

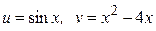
27.

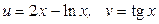
28.

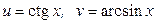
29.

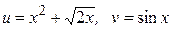
30.

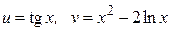
ЗАВДАННЯ 2 Знайти 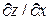 та 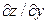, використовуючи правило диференціювання складної функції, якщо 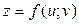, де , .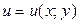

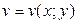1.

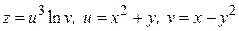
2.

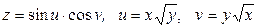
3.

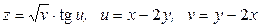
4.

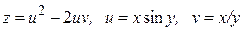
5.

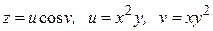
6.

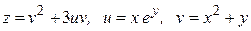
7.

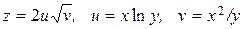
8.

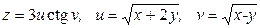
9.

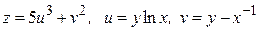
10.

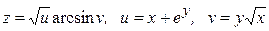
11.

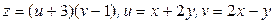
12.

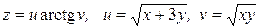
13.

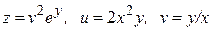
14.

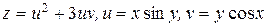
15.

 

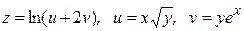
16.

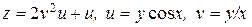
17.

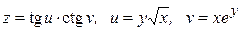
18.

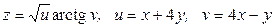
19.

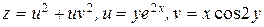
20.

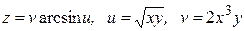
21.

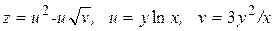
22.

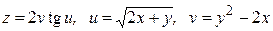
23.

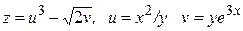
24.

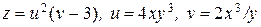
25.

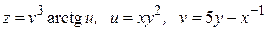
26.

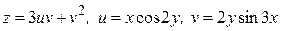
27.

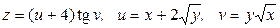
28.

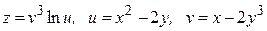
29.

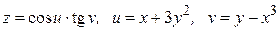
30.

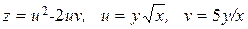
ЗАВДАННЯ 3         Поверхню S задано рівнянням 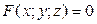. Потрібно пересвідчитися, що точка 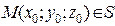, та знайти нормальний вектор  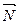до поверхні S в точці M, що утворює гострый кут з віссю Oz. Написати рівняння дотичної площини та нормалі до поверхні S в точці M.

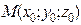
№	S		№	S
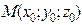
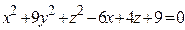
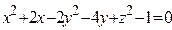
1.		(3; 0; –4)	2.		(1; 1; 2)
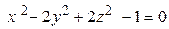
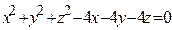
3.		(1; 1; 1)	4.		(4; 4; 0)
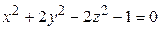
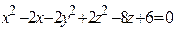
5.		(1; 2; 2)	6.		(2; 0; 3)
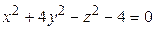
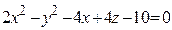
7.		(-2; 0, 5; 1)	8.		(3; 4; 5)
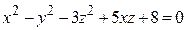
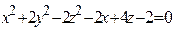
9.		(2; 2; 4)	10.		(0; 1; 2)
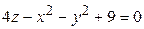
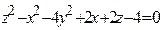
11.		(2; 1; –1)	12.		(–1; 0, 5; 2)
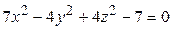
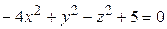
13.		(1; 1; 1)	14.		(0, 5; 0; -2)
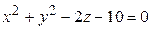
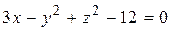
15.		(2; 2; –1)	16.		(4; 2; 2)
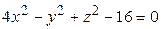
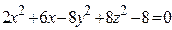
17.		(1; –2; 4)	18.		(1; 2; 2)
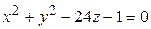
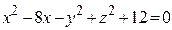
19.		(3; 4; 1)	20.		(2; 1; 1)
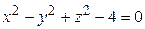
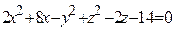
21.		(1; 1; –2)	22.		(2; 3; 1)
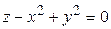
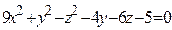
23.		(1; 1; 0)	24.		(0; –4; 3)
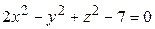
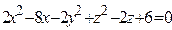
25.		(0; –3; 4)	26.		(3; 0; 2)
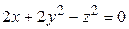
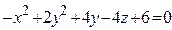
27.		(4; 2; 4)	28.		(4; 3; 5)
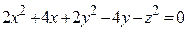
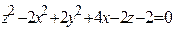
29.		(1; 1; 2)	30.		(2; 1; 0)

ЗАВДАННЯ 4. Задано скалярне поле 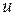, напрямок  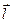та точка  :

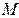а) Знайти 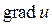, повний диференціал та похідну за напрямком  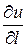в точці .

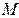б) Від функції 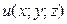 знайти частинні похідні другого порядку 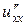, , 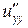, 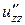а також мішану похідну вказану у таблиці.

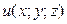
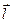
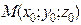
№				мішана похідна
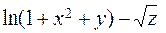
1.		(1; 1; 2)	(-3; 0; 4)
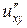
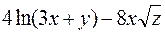
2.		(4; 4; 0)	(1; 1; 1)
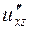
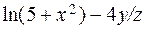
3.		(2; 0; 3)	(1; 2; 2)
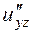
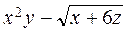
4.		(3; 4; 5)	(-2; 0, 5; 3)
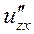
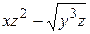
5.		(0; 1; 2)	(4; 2; 2)
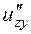
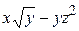
6.		(–1; 0, 5; 2)	(2; 1; –1)
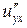
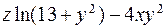
7.		(0, 5; 0; –2)	(1; 1; 1)
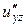
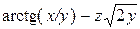
8.		(4; 2; 2)	(2; 2; –1)
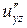
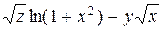
9.		(1; 2; 2)	(1; –2; 4)
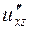
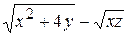
10.		(2; 1; 1)	(3; 4; 1)
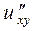
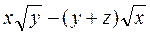
11.		(2; 3; 1)	(1; 1; –2)
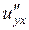
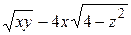
12.		(0; –4; 3)	(1; 1; 0)
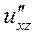
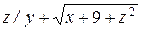
13.		(3; 0; 2)	(0; –3; 4)
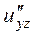
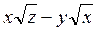
14.		(4; 3; 5)	(4; 2; 4)
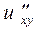
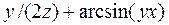
15.		(2; 1; 0)	(0; 1; 2)
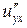
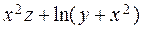
16.		(3; 0; –4)	(1; 1; 2)
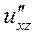
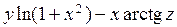
17.		(1; 1; 1)	(4; 4; 0)
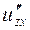
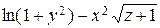
18.		(1; 2; 2)	(2; 0; 3)
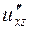
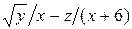
19.		(-2; 0, 5; 1)	(3; 4; 5)
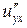
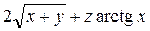
20.		(2; 2; 4)	(0; 1; 2)
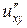
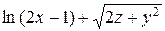
21.		(2; 1; –1)	(1; 0, 5; 3)
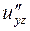
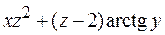
22.		(1; 1; 1)	(0, 5; 0; -2)
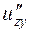
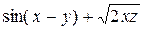
23.		(2; 2; –1)	(4; 2; 2)
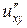
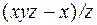
24.		(1; –2; 4)	(1; 2; 2)
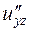
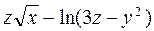
25.		(3; 4; 1)	(9; 1; 1)
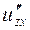
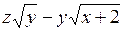
26.		(1; 1; –2)	(2; 1; -3)
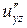
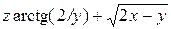
27.		(1; 1; 0)	(0; –4; 3)
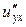
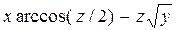
28.		(0; –3; 4)	(3; 4; 0)
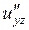
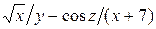
29.		(4; 2; 4)	(4; 3; 0)
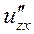
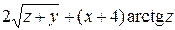
30.		(1; 1; 2)	(2; 1; 0)

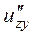
ЗАВДАННЯ 5 Дослідити функцію 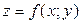 на екстремуми та обчислити її екстремальні значення.

1.

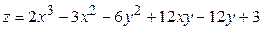
2.

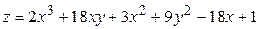
3.

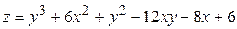
4.

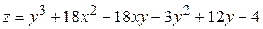
5.

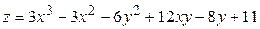
6.

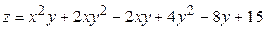
7.

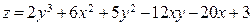
8.

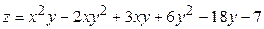
9.

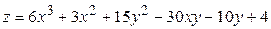
10.

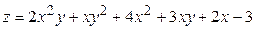
11.

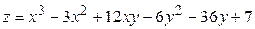
12.

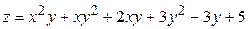
13.

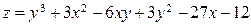
14.

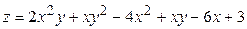
15.

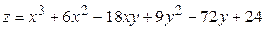
16.

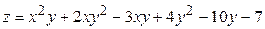
17.

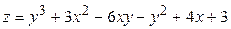
18.

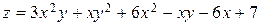
19.

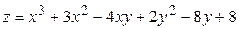
20.

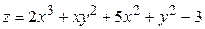
21.

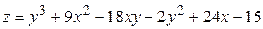
22.

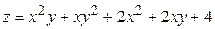
23.

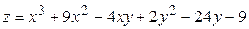
24.

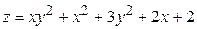
25.

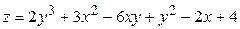
26.

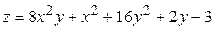
27.

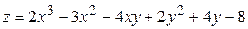
28.

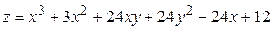
29.

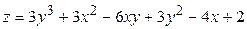
30.

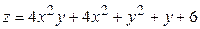
ЗАВДАННЯ 6   Для значень 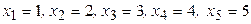 задано відповідні значення 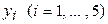. Потрібно за цими даними знайти за допомогою метода найменьших квадратів рівняння лінійной залежності 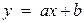. Представити експерементальні данні та шукану лінію на малюнку.

№
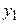
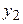
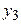
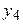
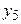
1.	0, 89	3, 62		4, 99		6, 48		9, 25
2.	1, 12	3, 59		4, 41		6, 75		9, 02
3.	0, 98	2, 89		4, 51		7, 49		9, 11
4.	1, 63	2, 77		5, 25		6, 37		9, 72
5.	1, 17	2, 83		5, 01		6, 48		9, 52
6.	0, 98	2, 68		5, 03		6, 88		9, 22
7.	1, 07	3, 17		5, 01		6, 83		8, 93
8.	0, 97	3, 03		5, 13		7, 23		8, 97
9.	1, 06	2, 94		4, 84		6, 92		9, 05
10.	0, 76	2, 66		5, 24		7, 34		8, 96
11.	1, 39	2, 42		2, 35		3, 32		3, 37
12.	1, 62	1, 81		2, 41		3, 16		4, 02
13.	1, 19	1, 89		2, 59		3, 12		3, 39
14.	1, 73	2, 12		2, 27		2, 87		3, 52
15.	1, 67	1, 83		2, 77		2, 68		3, 39
16.	1, 48	1, 68	2, 53		2, 88		3, 72
17.	1, 57	2, 17	2, 51		2, 83		3, 43
18.	1, 47	2, 03	2, 63		3, 23		3, 47
19.	1, 56	1, 94	2, 34		2, 92		3, 55
20.	1, 26	1, 66	2, 74		3, 34		3, 46
21.	0, 39	2, 42	3, 35		5, 32		6, 37
22.	0, 62	1, 81	3, 41		5, 16		7, 02
23.	0, 19	1, 89	3, 59		5, 12		6, 39
24.	0, 73	2, 12	3, 27		4, 87		6, 52
25.	0, 67	1, 83	3, 77		4, 68		6, 39
26.	0, 48	1, 68	3, 53		4, 88		6, 72
27.	0, 57	2, 17	3, 51		4, 83		6, 43
28.	0, 47	2, 03	3, 63		5, 23		6, 47
29.	0, 56	1, 94	3, 34		4, 92		6, 55
30.	0, 26	1, 66	3, 74		5, 34		6, 46

ЗАВДАННЯ 7 Знайти найбільше та найменьше значення функції 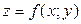 в замкнутій області, обмеженій вісями координат та прямою φ (x; y)=0.

№			№
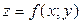
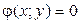
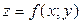
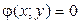
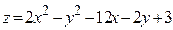
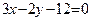
1.			2.
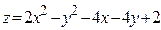
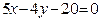
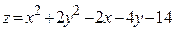
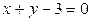
3.			4.
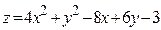
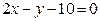
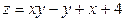
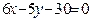
5.			6.
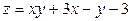
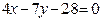
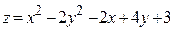
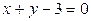
7.			8.
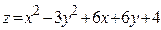
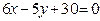
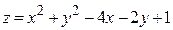
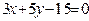
9.			10.
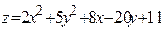
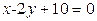
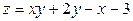
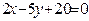
11.			12.
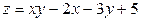
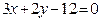
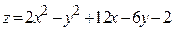
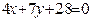
13.			14.
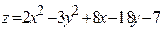
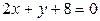
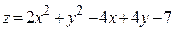
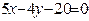
15.			16.
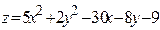
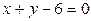
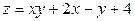
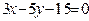
17.			18.
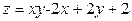
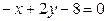
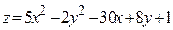
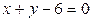
19.			20.
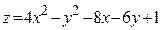
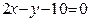
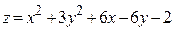
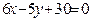
21.			22.
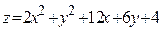
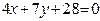
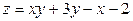
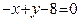
23.			24.
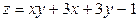
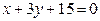
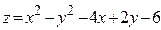
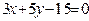
25.			26.
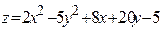
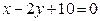
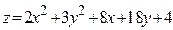
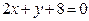
27.			28.
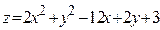
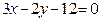
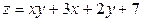
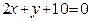
29.			30.

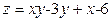
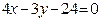
РоБОЧИЙ ЗОШИТ

Завдання 1. Обчислити 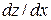, використовуючи правило диференціювання складної функції, якщо ,         ,

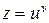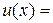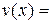
Розв‘язок. Обчислимо похідні:

                     

                     

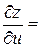
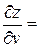
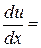
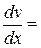
За формулою (2) знаходимо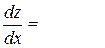  

Завдання 2. Використовуючи правило диференціювання складної функції, знайти 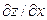 та 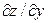, якщо  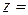                , де            ,           .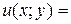

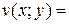Розв‘язок. Обчислимо частинні похідні:

                                                            

 

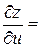
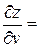
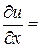
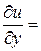
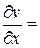
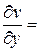
За формулами (3) знаходимо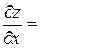  

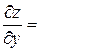
Завдання 3. Поверхню S задано рівнянням 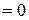                                   . Потрібно пересвідчитися, що точка 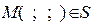, та знайти нормальний вектор  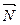до поверхні S в точці M, що утворює гострый кут з оссю Oz. Написати рівняння дотичної площини та нормалі до поверхні S в точці M.

Розв‘язок. Перевіремо, що точка 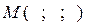 належить поверхні S . Для цього підставимо координати точки М до рівняння поверхні:

Знайдемо нормальний вектор до поверхні S в точці М. Для цього обчислимо такі частинні похідні та їх значення в точці М:

                                                                       

                                                                       

                                                                       

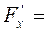
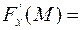
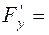
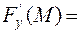
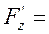
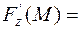
Отже нормальний вектор до поверхні S в точці М має координати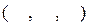

Для того, щоб вектор утворював гострий кут з віссю OZ необхідно, щоб третя координата цього вектора була додатня, отже якщо це не так, треба помножити одержаний вектор 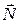 на коефіцієнт (-1).

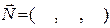
За формулою (13) запишемо рівняння дотичної площіни до поверхні S в точці М

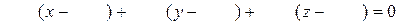
За формулою (12) запишемо рівняння нормалі до поверхні S в точці М

;

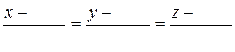Завдання 4. Задано скалярне поле 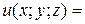                                                  та напрямок :

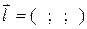а) Знайти 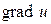 повний диференціал та похідну за напрямком  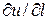в точці М( ; ;   ).

б) Знайти частинні похідні другого порядку 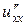, , 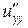 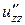від функції 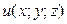, а також мішану похідну вказану у таблиці   .

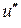Розв‘язок. а)Знайдемо частинні похідні функції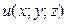  

 

 

 

 

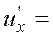
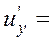
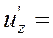
За формулою (7) градієнт функції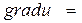

 

обчислимо значення градієнта функції в точці М .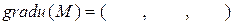

За формулою ( 1 ) повний диференціал  

 його значення в точці М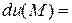

Для знаходження похідної за напрямком, знайдемо довжину вектора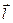  

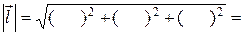
Далі за формулами (6) напрямні косинуси вектора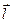  

, ,

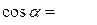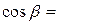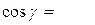
За формулою (5) похідна за напрямком 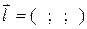 дорівнює:

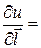
її значення в точці М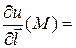

б) Знайдемо похідні другого порядку 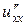, , 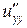 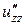від функції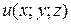

 

 

 

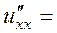
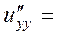
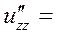
а також мішану похідну вказану у таблиці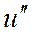   

 

 

Завдання 5.  Дослідити функцію 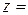                                                            на екстремуми та обчислити экстремальні значення.

Розв‘язок. Знайдемо стаціонарні точки, для цього обчислимо частинні похідні

                                                        

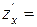
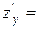
прирівняємо ці похідні до нуля та розв‘яжемо систему ;

 

Перевіремо чи набуває функціяє в отриманих стаціонарних точках екстремумів. Для цього обчислемо другі частинні похідні:

 

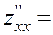
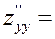
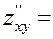
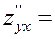
Обчислемо значення цих похідних ( 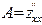; ; 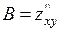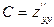) в кожній стаціонарній точці окремо, після цього знайдемо значення визначника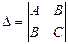  

Завдання 6. Задано таблицю

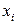
	1	2	3	4	5

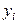
Потрібно знайти за допомогою метода найменьших квадратів рівняння лінійной залежності 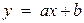. Представити експерементальні данні та шукану лінію на малюнку

Розв‘язок. За формулами (15)  знаходимо

              ,      

 

                            

 

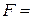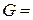
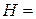
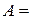
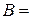
Далі з системи (16): 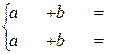, знаходимо  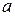та :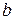

Таким чином, шукана залежність має вигляд 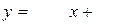. Представимо знайдену лінійну залежність і експерементальні дані на малюнку

⇐ Предыдущая12345

Поделиться: