Графическая иллюстрация решений

 

В данном случае все численные решения ОДУ весьма близки к точному решению.

5.6. Контрольные вопросы по теме
Методы решения дифференциальных уравнений

1. Что такое обыкновенное дифференциальное уравнение?
2. Что такое порядок ОДУ?
3. Что называется аналитическим решением ОДУ 1-го порядка?
4. Что является общим решением ОДУ ?
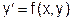5. Что является геометрической интерпретацией общего решения ОДУ ?
6. Что является частным решением ОДУ ?
7. Что является численным решением ОДУ ?
8. Что относится к начальным условиям при решении ОДУ 1-го порядка численными методами?
9. Имеет ли задача Коши для дифференциального уравнения 1-го порядка единственное решение?
10. По какому правилу проводят оценку погрешности решения методов Рунге-Кутты?
11. Как выглядит формула для определения очередного значения функции по методу Рунге-Кутты 1-го порядка?
12. Уменьшение шага интегрирования при использовании методов Рунге-Кутты приводит к уменьшению или увеличению погрешности?
13. В обыкновенном дифференциальном уравнении присутствуют производные разных порядков от одной переменной или только первая производная от нескольких переменных?
14. Методы Рунге-Кутты являются одношаговыми или двухшаговыми методами?
15. Сколько раз на каждом шаге необходимо вычислять  в модифицированном методе Эйлера?
16. Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании одного или двух предыдущих значений функции?
17. Возможно ли в методах Рунге-Кутты применение переменного шага интегрирования?
18. Процесс решения дифференциального уравнения называется интегрированием или дифференцированием?
19. Каковы формулы оценки погрешности методов Рунге-Кутты?
20. Почему метод Эйлера называют методом Рунге-Кутты первого порядка?
21. Модифицированный метод Эйлера иначе называется методом Рунге-Кутты решения ОДУ 1-го или 2-го порядка?
22. Что требуется предварительно сделать, чтобы применить методы Рунге-Кутты при решении ОДУ 2-го порядка?
23. С помощью какого параметра происходит достижение заданной точности решения ОДУ в методе автоматического выбора шага?
24. Можно ли оценить погрешность решения ОДУ, не зная точного решения?
25. В каком методе решения ОДУ подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников?
26. В каком методе решения ОДУ подынтегральная функция на отрезке [x_i;x_i+1] аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом трапеции?
27. Что является начальными условиями ОДУ n-го порядка (для n=2)?

28. Сколько ОДУ 1-го порядка будет содержать система, построенная для решения n-го

порядка?

⇐ Предыдущая123

Поделиться: