Геометричні властивості мішаного добутку

Приклади.

Задано вектори 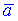та . Обчислити їх скалярний добуток, якщо

1)

2)

3)

4)

5)

6)

7)

Розв'язання. Виконаємо обчислення згідно першого означення.

1)

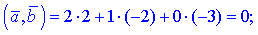
2)

3)

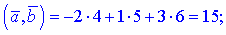
4)

5)

6)

7)

 

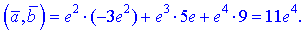
ІV. Векторним добутком 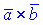або двох векторів називається вектор 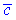, який відповідає наступним умовам:
1) модуль вектора 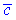рівний добутку модулів векторів і на синус кута між ними

2) вектор 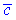нормальний до площини, побудованої на векторах і ;
3) вектор напрямлений так, що з його кінця найкоротший поворот від вектора до відбувається проти руху годинникової стрілки. Іншими словами, вектори утворюють праву трійку.

Векторний добуток має наступні геометричні властивості:
Його модуль рівний площі паралелограма побудованого на векторах і

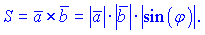
Тому площа трикутника, побудованого на векторах і рівна модулю половини векторного добутку цих векторів

Алгебраїчні властивості векторного добутку

1) векторний добуток 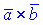рівний нулю у випадку колінеарності векторів та коли один з них нульовий;
2) від перестановки векторів векторний добуток змінює знак на протилежний:

3)
4)

На практиці важливо мати під рукою формулу для обчислення векторного добутку в координатній формі, тому запишемо і її


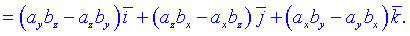
Розглянемо конкретні приклади для засвоєння пройденого матеріалу.

 

Приклад 1. Задано вектори та
Знайти наступні величини
1) суму векторів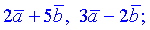
2) скалярний добуток векторів
3) векторний добуток площу трикутника побудованого на векторах
4) кут між векторами
5) проекцію кожного з векторів на інший

Розв'язок. 1) Проведемо обчислення


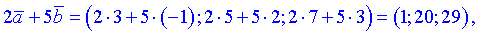
2) Скалярний добуток буде рівний

3) Векторний добуток обчислюємо згідно формули



Площа трикутника буде рівна

4) Знайдемо кут між векторами за

У ній скалярний добуток вже знайдений, тож знаходимо довжини векторів


Підставляємо потрібні значення у формулу

Знаходимо значення кута

5) Знайдемо проекції векторів


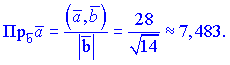
Проекції векторів можна шукати через косинус кута між векторами, результат від цього не зміниться

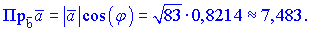
Мішаним добутком трьох векторів називається число, яке рівне векторному добутку перших двох векторів 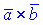, помноженому скалярно на третій вектор 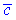. Векторно це можна подати формулою

Так як вектори на практиці задають в координатній формі, то їх мішаний добуток рівний визначникові, побудованому на координатах векторів

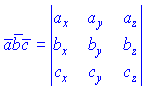
В силу того, що векторний добуток антикомутативний, а скалярний добуток комутативний, то циклічна перестановка векторів в мішаному добутку не змінює його значення. Перестановка двох сусідніх векторів змінює знак на протилежний


Запам'ятайте наступне правило: мішаний добуток векторів додатній, якщо вони утворюють праву трійку та від'ємний – якщо ліву.

Проекція вектора на вісь

Основні поняття

Н ехай у просторі задана вісьl, тобто спрямована пряма. Проекцією точки М на вісь l називається основа перпендикуляра , опущеного із точки на вісь.

Точка єточкою перетину осі l із площиною, що проходить через точку М перпендикулярно осі.

Якщо точка М лежить на осі , то проекція точки М на вісь збігається з М.

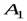Нехай – довільний вектор ( ). Позначимо через і проекції на вісь відповідно до початку А і кінця В вектора й розглянемо вектор (рис. 2.7).

Рисунок 2.7

Проекцією вектора 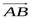на вісь називається додатне число , якщо вектор і вісьl однаково спрямовані й від'ємне число , якщо вектор 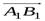і вісь l протилежно спрямовані. Якщо точки й збігаються ( =0), то проекція вектора 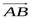дорівнює 0.

Проекція вектора на вісь позначається так: . Таким чином, із означення маємо

Кут між вектором і віссю l (або кут між двома векторами) зображений на рис. 2.8. Очевидно, що .

Рисунок 2.8

Властивості проекцій

1. Проекція вектора на вісь дорівнює добутку модуля вектора на косинус кута між вектором та віссю, тобто

.

Доведення.

Якщо 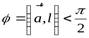, то .

Якщо , то .

Якщо , то .

Наслідки.

1. Проекція вектора на вісь додатна (від'ємна), якщо вектор утворює з віссю гострий (тупий) кут, і дорівнює нулю, якщо цей кут – прямий.

2. Проекції рівних векторів на ту саму вісь рівні між собою.

2. Проекція суми декількох векторів на ту саму вісь дорівнює сумі їхніх проекцій на цю вісь, тобто

.

Доведення.

Н ехай, наприклад, . Маємо

, тобто .

3. При множенні вектора на число 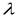його проекція на вісь також помножується на це число, тобто

.

Доведення.

При : .

При : .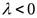

При властивість очевидна.

Таким чином, лінійні операції над векторами приводять до відповідних лінійних операцій над проекціями цих векторів.

Означення.

Напрямні косинуси вектора (направляючі косинуси вектора) a – це косинуси кутів, які вектор утворює з додатними півосями координат.

Напрямні косинуси однозначно задають напрямок вектора.

Основне співвідношення.

Щоб знайти напрямні косинуси вектора a необхідно відповідні координати вектора поділити на модуль вектора.

Відповідні координати одиничного вектора дорівнюють його напрямними косинусам.

Приклади.

Задано вектори 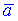та . Обчислити їх скалярний добуток, якщо

1)

2)

3)

4)

5)

6)

7)

Розв'язання. Виконаємо обчислення згідно першого означення.

1)

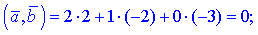
2)

3)

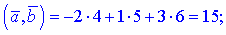
4)

5)

6)

7)

 

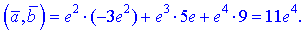
ІV. Векторним добутком 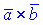або двох векторів називається вектор 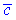, який відповідає наступним умовам:
1) модуль вектора 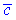рівний добутку модулів векторів і на синус кута між ними

2) вектор 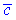нормальний до площини, побудованої на векторах і ;
3) вектор 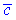напрямлений так, що з його кінця найкоротший поворот від вектора до відбувається проти руху годинникової стрілки. Іншими словами, вектори утворюють праву трійку.

Векторний добуток має наступні геометричні властивості:
Його модуль рівний площі паралелограма побудованого на векторах і

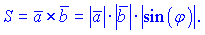
Тому площа трикутника, побудованого на векторах і рівна модулю половини векторного добутку цих векторів

Алгебраїчні властивості векторного добутку

1) векторний добуток 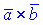рівний нулю у випадку колінеарності векторів та коли один з них нульовий;
2) від перестановки векторів векторний добуток змінює знак на протилежний:

3)
4)

На практиці важливо мати під рукою формулу для обчислення векторного добутку в координатній формі, тому запишемо і її


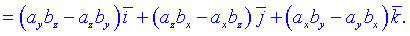
Розглянемо конкретні приклади для засвоєння пройденого матеріалу.

 

Приклад 1. Задано вектори та
Знайти наступні величини
1) суму векторів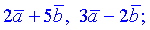
2) скалярний добуток векторів
3) векторний добуток площу трикутника побудованого на векторах
4) кут між векторами
5) проекцію кожного з векторів на інший

Розв'язок. 1) Проведемо обчислення


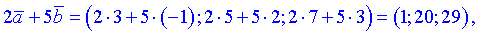
2) Скалярний добуток буде рівний

3) Векторний добуток обчислюємо згідно формули



Площа трикутника буде рівна

4) Знайдемо кут між векторами за

У ній скалярний добуток вже знайдений, тож знаходимо довжини векторів


Підставляємо потрібні значення у формулу

Знаходимо значення кута

5) Знайдемо проекції векторів


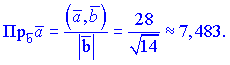
Проекції векторів можна шукати через косинус кута між векторами, результат від цього не зміниться

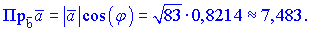
Мішаним добутком трьох векторів називається число, яке рівне векторному добутку перших двох векторів 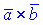, помноженому скалярно на третій вектор 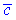. Векторно це можна подати формулою

Так як вектори на практиці задають в координатній формі, то їх мішаний добуток рівний визначникові, побудованому на координатах векторів

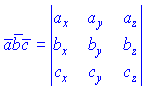
В силу того, що векторний добуток антикомутативний, а скалярний добуток комутативний, то циклічна перестановка векторів в мішаному добутку не змінює його значення. Перестановка двох сусідніх векторів змінює знак на протилежний


Запам'ятайте наступне правило: мішаний добуток векторів додатній, якщо вони утворюють праву трійку та від'ємний – якщо ліву.

Геометричні властивості мішаного добутку

1. Об'єм паралепіпеда, побудованого на векторах рівний модулю мішаного добутку цих векторів

2. Об'єм чотирикутної піраміди рівний третині модуля мішаного добутку

3. Об'єм трикутної піраміди рівний одній шостій модуля мішаного добутк

4. Умова компланарності векторів: три вектори компланарні тоді і лише тоді, коли їх мішаний добуток рівний ную

В координатах умова компланарності означає рівність нулю визначника

На цьому оротка теорія завершена і можна переходити до практичних занять.

 

123Следующая ⇒

Поделиться: