
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ КОМБИНАЦИОННОГО И ПОСЛЕДОВАТЕЛЬНОСТНОГО ТИПОВ
Лабораторный практикум по дисциплине «Цифровые вычислительные устройства и микропроцессоры приборных комплексов»
Уфа 2006 Составитель: В.В. Неретина
УДК 681.3.06 ББК 32.97
Проектирование цифровых устройств комбинационного и последовательностного типов: Лабораторный практикум по дисциплине «Цифровые вычислительные устройства и микропроцессоры приборных комплексов» / Уфимск. гос. авиац. техн. ун-т; Сост.: В.В. Неретина. – Уфа, 2006. – 44 с.
В методических указаниях приведено описание лабораторных работ, позволяющих студентам изучить основы математической логики и методы синтеза комбинационных и последовательностных устройств. Исследование цифровых устройств осуществляется путем моделирования в среде пакета Simulink системы MATLAB. Предназначены для студентов, обучающихся по направлению подготовки дипломированных специалистов 200100 – «Приборостроение» по специальности 200103 – «Авиационные приборы и измерительно-вычислительные комплексы».
Табл. 21. Ил. 31. Библиогр.: 11 назв.
Рецензенты: канд. техн. наук, доц. Нугаев Р.Р., канд. техн. наук, доц. Озеров В.В.
© Уфимский государственный авиационный технический университет, 2006
СОДЕРЖАНИЕ Введение............................................................................................................. 4 1. Лабораторная работа № 1 «Проектирование цифровых устройств комбинационного типа»............................................................... 5 1.1. Цель работы............................................................................................... 5 1.2. Теоретическая часть................................................................................. 5 1.2.1. Основы булевой алгебры..................................................................... 5 1.2.2. Формы представления логических функций.................................... 8 1.2.3. Синтез комбинационных устройств................................................. 14 1.3. Описание среды моделирования Simulink......................................... 19 1.4. Порядок выполнения работы............................................................... 19 1.5. Требования к отчету............................................................................... 22 1.6. Контрольные вопросы........................................................................... 22 2. Лабораторная работа № 2 «Проектирование цифровых устройств последовательного типа».......................................................... 23 2.1. Цель работы............................................................................................. 23 2.2. Теоретическая часть............................................................................... 23 2.2.1. Триггеры: классификация и способы описания функционирования........................................................................................ 23 2.2.2. Счетчики: классификация и основные параметры......................... 29 2.2.3. Синтез синхронных двоичных счетчиков....................................... 31 2.2.4. Синтез синхронных десятичных счетчиков.................................... 36 2.3. Описание среды моделирования Simulink......................................... 38 2.4. Порядок выполнения работы............................................................... 40 2.5. Требования к отчету............................................................................... 41 2.6. Контрольные вопросы........................................................................... 42 Список литературы........................................................................................ 43 ВВЕДЕНИЕ В современной науке и технике важнейшую роль играют цифровые методы обработки информации. В связи с этим непрерывно расширяется область применения цифровых систем и, как следствие, развивается цифровая техника, изучающая принципы построения, методы проектирования и способы технической реализации цифровых систем. При этом цифровая техника использует достижения смежных фундаментальных и прикладных наук, таких как математическая логика, кибернетика, электроника и др. В общем случае устройства, оперирующие с двоичной информацией, подразделяются на два больших класса: комбинационные схемы (дискретные автоматы без памяти) и последовательностные устройства (дискретные автоматы с памятью). В настоящем лабораторном практикуме изучаются методы проектирования цифровых комбинационных и последовательностных устройств. В связи с этим в первой лабораторной работе рассматривается математический аппарат, описывающий действия дискретных устройств, формы представления логических функций, методы минимизации с помощью карт Карно и представления функций в различных базисах (И, ИЛИ, НЕ; И–НЕ, ИЛИ–НЕ), а также примеры синтеза комбинационных устройств на логических элементах и мультиплексорах. На основании изложенного теоретического материала даны задания, выполнения которых позволяет студентам закрепить полученные знания путем моделирования в среде пакета Simulink системы MATLAB созданных ими схем. Во второй лабораторной работе помимо сведений о принципах функционирования и параметрах последовательностных устройств, на конкретных примерах приводятся методы анализа и синтеза синхронных счетчиков с различными коэффициентами счета. Также даны варианты заданий для реализации в пакете Simulink. Лабораторный практикум составлен в соответствии с требованиями типовой учебной программы по дисциплине «Цифровые вычислительные устройства и микропроцессоры приборных комплексов», рекомендованной Министерством образования и науки РФ по направлению подготовки дипломированных специалистов 200100 – «Приборостроение» специальности 200103 – «Авиационные приборы и измерительно-вычислительные комплексы». 1. ЛАБОРАТОРНАЯ РАБОТА № 1 «ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ КОМБИНАЦИОННОГО ТИПА» Цель работы Целью работы является ознакомление студентов с математическим аппаратом, описывающим действия цифровых устройств, развитие навыков составления логических уравнений, их минимизации, а также реализации на основе полученных уравнений комбинационных устройств с учетом имеющегося набора логических элементов. Теоретическая часть Основы булевой алгебры Математический аппарат, описывающий действия дискретных устройств, базируется на алгебре логики, или булевой алгебре. Булева алгебра оперирует двоичными переменными, которые условно обозначаются как 0 и 1, и подчиняются условию: Действия над двоичными переменными производятся по правилам логических операций. Простейших логических операций три: отрицание (инверсия, операция НЕ), логическое умножение (конъюнкция, операция И) и логическое сложение (дизъюнкция, операция ИЛИ). Более сложные логические преобразования можно свести к указанным операциям. Операция отрицания выполняется над одной переменной и характеризуется следующими свойствами: функция Операция логического умножения (конъюнкция) для двух переменных Операцию логического сложения (дизъюнкции) Совокупность различных значений переменных называют набором. Булева функция Таблица 1.1 Таблица 1.2 Операция конъюнкции Операция дизъюнкции
Два аргумента дают 16 значений функций (таблица 1.3). Таблица 1.3 Система функций двух переменных
Функция |
Название функции | |||||||||||||||||||||||||||||||||||||||

| 0 | 1 | 0 | 1 | ||||||||||||||||||||||||||||||||||||

| 0 | 0 | 0 | 0 | 
| Константа 0 | ||||||||||||||||||||||||||||||||||
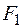
| 0 | 0 | 0 | 1 | 
| Конъюнкция, операция И | ||||||||||||||||||||||||||||||||||

| 0 | 0 | 1 | 0 | 
| Запрет по 
| ||||||||||||||||||||||||||||||||||

| 0 | 0 | 1 | 1 | 
| Тождественность
(тавтология) 
| ||||||||||||||||||||||||||||||||||
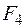
| 0 | 1 | 0 | 0 | 
| Запрет по 
| ||||||||||||||||||||||||||||||||||

| 0 | 1 | 0 | 1 | 
| Тождественность
(тавтология) 
| ||||||||||||||||||||||||||||||||||

| 0 | 1 | 1 | 0 | 
| Исключающее ИЛИ (сумма по модулю 2) | ||||||||||||||||||||||||||||||||||

| 0 | 1 | 1 | 1 | 
| Дизъюнкция, операция ИЛИ | ||||||||||||||||||||||||||||||||||

| 1 | 0 | 0 | 0 | 
| Стрелка Пирса (операция ИЛИ–НЕ) |
Окончание таблицы 1.3
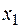
| 0 | 0 | 1 | 1 |
Функция |
Название функции |

| 0 | 1 | 0 | 1 | ||

| 1 | 0 | 0 | 1 | 
| Равнозначность, эквивалентность |

| 1 | 0 | 1 | 0 | 
| Инверсия 
|

| 1 | 0 | 1 | 1 | 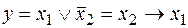
| Импликация от  к к 
|
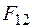
| 1 | 1 | 0 | 0 | 
| Инверсия 
|

| 1 | 1 | 0 | 1 | 
| Импликация от  к к 
|
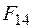
| 1 | 1 | 1 | 0 | 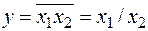
| Штрих Шеффера (операция И–НЕ) |

| 1 | 1 | 1 | 1 | 
| Константа 1 |
Булева алгебра базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с двоичными переменными. Обоснованность выбора этих аксиом подтверждается таблицами истинности для рассмотренных операций. Каждая аксиома представлена в двух видах, что вытекает из принципа дуальности (двойственности) логических операций, согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять логическую 1 на 0, 0 на 1, знак  на ∙, а ∙ на
на ∙, а ∙ на  .
.
Аксиомы операции отрицания:  ,
,  .
.
Аксиомы операций конъюнкции и дизъюнкции:
1.  ;
;  ; (1.1)
; (1.1)
2.  ;
;  ; (1.2)
; (1.2)
3. 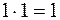 ;
;  . (1.3)
. (1.3)
Законы булевой алгебры вытекают из аксиом и также имеют две формы выражения: для конъюнкции и дизъюнкции. Их правильность легко проверить по таблицам истинности либо путем подстановки 0 и 1 вместо соответствующих значений переменных.
1. Переместительный закон
 ;
; 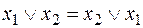 . (1.4)
. (1.4)
2. Сочетательный закон
 ;
;
 . (5.5)
. (5.5)
3. Закон повторения (тавтологии)
 ;
; 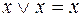 . (1.6)
. (1.6)
4. Закон обращения: если  , то
, то  . (1.7)
. (1.7)
5. Закон двойной инверсии  . (1.8)
. (1.8)
6. Закон нулевого множества
 ;
;  . (1.9)
. (1.9)
7. Закон универсального множества
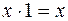 ;
; 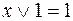 . (1.10)
. (1.10)
8. Закон дополнительности
 ;
;  . (1.11)
. (1.11)
9. Распределительный закон
 ;
; 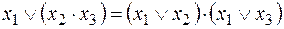 . (1.12)
. (1.12)
10. Закон поглощения
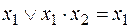 ;
;  . (1.13)
. (1.13)
11. Закон склеивания
 ;
;  . (1.14)
. (1.14)
12. Закон инверсии (закон Де Моргана)
 ;
;  (1.15)
(1.15)
или после инвертирования левых и правых частей
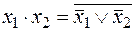 ;
;  . (1.16)
. (1.16)
Последнее изменение этой страницы: 2019-04-19; Просмотров: 428; Нарушение авторского права страницы