Разложение в ряд Фурье непериодической функции.

Задача разложения непериодической функции в ряд Фурье,  в принципе не отличается от разложения в ряд Фурье периодической функции.

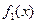Допустим, что функция f ( x ) задана на отрезке  и является на этом отрезке  кусочно - монотонной.  Рассмотрим произвольную периодическую кусочно - монотонную функцию  c периодом , совпадающую с функцией f ( x ) на отрезке . То есть можно подобрать отрезок 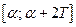, содержащий отрезок  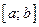и раскладывать в ряд Фурье функцию на это отрезке.

 

                                                       y

                                                                   f(x)

 

 

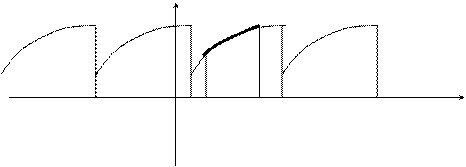
                               a - 2T                a a     b a+2T         a + 4T        x

 

Таким образом, функция  f ( x ) была доопределена.  Полученная  функция  разлагается в ряд Фурье на отрезке 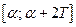, являясь периодической с периодом 2T.  Сумма ряда, составленного для функции , во всех точках отрезка 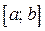 совпадает с функцией f ( x ), поэтому можно считать, что функция f ( x ) разложена в ряд Фурье на отрезке .

Если функция f ( x ) задана на отрезке, равном  2l, то ее разложение ничем не отличается от разложения в ряд периодической функции с периодом 2l. Если же отрезок, на котором задана функция, меньше, чем  2l, то ее можно продолжить на отрезок [a ; a +2l ], так, чтобы условия разложимости в ряд Фурье сохранялись. Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2l  может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но все они будут совпадать с заданной функцией f ( x ) на отрезке .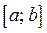

Пример 4 .  Разложить в ряд Фурье функцию .

Решение. Будем считать функцию периодической с периодом 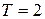, т.е. 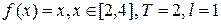. Построим график этой функции

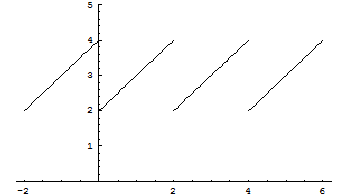
Тогда, ряд Фурье для этой функции будет иметь следующий вид: .

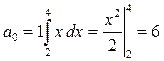
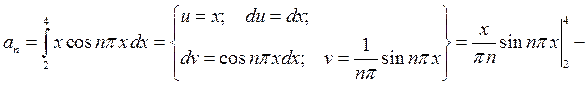
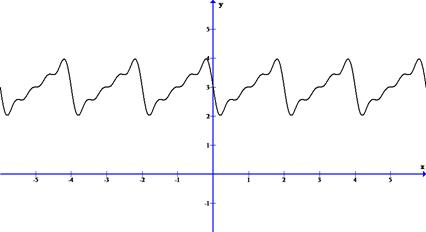
Таким образом .  Построим график S₃(x).

Вопросы для самопроверки

1. Запишите ряд Фурье для непериодической функции, заданной на некотором интервале (а, b).

§5. Задача о разложении в ряд Фурье функции, заданной на отрезке [0, π] ([0.l]) по синусам или по косинусам

Этот случай можно свести к предыдущему. Для решения задачи достаточно дополнить определение этой функции для значений  x в проме­жутке  по свободному выбору. Теперь уже  будет оп­ределена на отрезке . Далее поступаем так, как описано в  §3.  В силу того, что мы свободны в выборе вида функции на промежутке , то в результате будут получаться различные ряды Фурье в зависимости от этого выбора. Этот факт может быть использован для получения ряда Фурье функции , содержащего или только косинусы, или только синусы.

Если доопределить данную функцию так, чтобы при , то в результате получится четная функция в промежутке , разложение в ряд Фурье такой функции содержит только косинусы. Коэффициенты разложения можно вычислять по форму­лам: 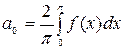, . Таким образом, заданную на отрезке  функцию  мы разложили по косинусам.

Если доопределить данную функцию так, чтобы  при 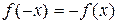, то в результате получится нечетная функция, рассматриваемая на промежутке . Разложение в ряд Фурье такой функции содержит только синусы. При этом коэффициенты разложения можно вычислять по формуле: . В этом случае функция , заданная на промежутке , будет разложена по синусам.

Графически это можно представить следующим образом:

Из сказанного следует: заданную на промежутке  функ­цию можно разлагать в ряд  Фурье  как по синусам, так и по ко­синусам.

Замечание 1. Нетрудно заметить, что как в случае разложения неперио­дической функции , определенной на отрезке , так и в случае ее разложения на отрезке  периодическое продолжение заданной функции можно и не осуществлять. На это указывают формулы, из которых определяют­ся коэффициенты Фурье. Но чтобы не сделать ошибок, рекомендуется иметь эскиз графика функции с ее четным или нечетным продолжением на про­межутке  и с последующим периодическим продолжением на всю чи­словую прямую.

Замечание 2. В случае разложения неперио­дической функции , определенной на отрезке 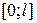 периодическое продолжение производится аналогично функции, определенной на . Формулы, из которых определяют­ся ряд и  коэффициенты Фурье, выбираются соответственно для нечетной функции:  ,

для четной функции.

Пример 5 . Разложить в ряд Фурье функцию 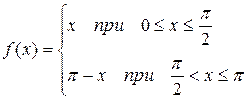   по синусам.

Решение. Продолжив заданную функцию  нечетным образом на промежуток , получим функцию, удовлетворяющую условиям Дирихле на отрезке длиной .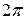

Найдем коэффициенты Фурье для этой функции. Так как она нечетна и, кроме того, симметрична относительно оси абсцисс при совмещении двух полупериодов, ее ряд Фурье содержит только нечетные синусоиды: , .

Окончательно получаем .

Построим график S₃(x)

Во многих задачах приходится разлагать в ряд Фурье функцию, заданную на промежутке . При этом функция  на этом промежутке оказывается не только непрерывной, но и дифференцируемой. В этом случае мы можем разложить в ряд Фурье данную функцию,  как по синусам, так и по косинусам. Спрашивается, какому разложению отдать предпочтение? Какой ряд будет обладать лучшими свойствами сходимости? Для практики решение этих вопросов имеет немаловажное значение.

Характер сходимости ряда Фурье определяется свойствами заданной функции в граничных точках  и . Если функция  в этих точках отлична от нуля, то периодическое продолжение ее по принципу нечетной функции приведет к разрыву в двух точкам  и . Эти разрывы легко ликвидируются, если определить  как четную функцию. По этой причине разложение в ряд по косинусам будет обладать гораздо лучшими свойствами сходимости, чем разложение по синусам. В этом случае коэффи­циенты ряда косинусов убывают со  скоростью 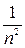 а коэффициен­ты ряда синусов - со скоростью .

Если теперь допустить, что  в точках  и  при­нимает значения, равные нулю, то разложение в ряд по синусам дает гораздо лучшую сходимость, чем разложение в ряд по коси­нусам, так как периодическое продолжение функции  по принципу нечетной функции обеспечивает непрерывность и самой функции и ее первой производной, в то время как периодическое продолжение по принципу четной функ­ции приводит к разрыву первой производной в точках  и . В этом случае  коэффициенты ряда синусов убывают со скоростью ,  подходящей для многих приложений рядов Фурье.

Вопросы для самопроверки

1. Запишите ряд Фурье для разложения  функции, заданной  на промежутке , по синусам и косинусам

⇐ Предыдущая12345Следующая ⇒

Поделиться: