Комплексная форма ряда Фурье

 

До сих пор речь шла о представлении функции  рядом Фурье по формуле: ,

 где .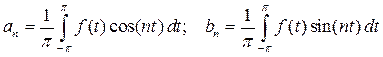

В приложениях преимущественно пользуются другой, более компактной формой записи функции  в виде ряда Фурье, назы­ваемой комплексной формой ряда Фурье. Получить эту новую форму помогают известные тождества Эйлера, устанавливающие связь между тригонометрическими и показательной функциями:

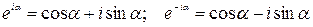
Отсюда 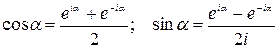. С помощью последних формул можно преобразовать общий член ряда: .

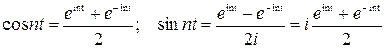Подставляя  вместо ,  найденные для них выражения в формулу (1), получим

Очевидно, при изменении знака  n    сохранит свой знак, а  поменяет его на противоположный, т.е.  -  четная, а 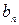 - нечетная функции относительно  n,  поэтому ; . Учитывая это,   записывают .

При  n = 0 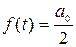. Обозначим , окончательно получим . Если учесть формулы Эйлера:

Т. о., ряд Фурье в комплексной форме имеет вид ,

где комплексный коэффициент (комплексная амплитуда) определяется по формуле .

Пример 6 . Разложить в комплексный ряд Фурье периодическую функцию с периодом , определенную следующим образом: , .

Решение. Построим график.

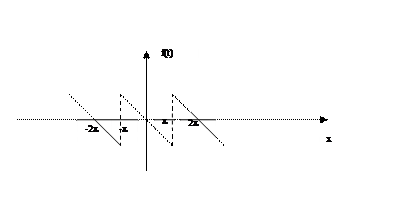
Проверив выполнение условий Дирихле для функции , переходим к вычислению коэффи­циентов Фурье по формуле .

Интеграл, стоящий в правой части последнего равенства, опре­деляется по частям:

;

Если , то полученные формулы не дают результата. Поэтому коэффициент   надо вычислить иначе׃ , так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим

Это равенство имеет место лишь в точках непрерывности функции . В точках разрыва , где  k- любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр

Вопросы для самопроверки

1. Запишите комплексную форму ряда Фурье

 §7. Амплитудно-частотный спектр ряда Фурье

 

Для приложений удобна другая, более компактная форма записи ряда Фурье: , здесь .

После введения этих обозначений ряд Фурье функции произвольного периода T примет вид , где .

 Из формулы видно, что сложная периодическая функция  вполне определяется совокупностью величин 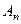 и 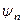, причем  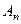- амплитуда n- й гармоники, а  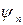– ее фаза. Совокупность величин  носит название спектра амплитуд, совокупность же величин 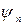 называется спектром фаз функции .

Рассмотрим амплитудный спектр  функции . (При рассмотрении приложений достаточно знать лишь спектр амплитуд.) Изобразим спектр периодической функции 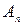 графически. Для этого выберем систему координат, назвав ось ординат осью 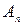, а ось абсцисс - осью ω. Так как каждому значению nω соответствует одно вполне определенное значение , то амплитуды отдельных гармоник изображают вертикальными отрезками определенной длины, как показано на рисунке.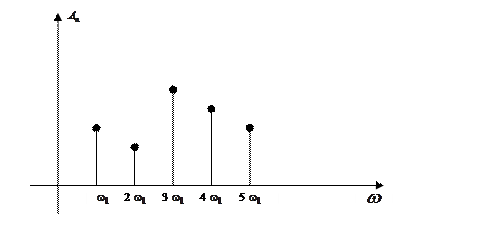

В приложениях часто встречаются задачи, приводящие к нахождению спектра некоторой периодической функции . При этом приходится иметь дело со спектрами самых разнообразных величин. Ведь теми или иными функциями времени могут выражаться изменения различных физических величин. Нахождение спектра периодического процесса и составляет его гармонический анализ.

Изучая спектр  функции  легко найти те значения ω, которым соответствуют большие значения 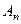, т.е. те частоты, которым соответствуют гармонические функции, играющие наибольшую роль в образовании данной функции  рядом Фурье.

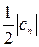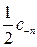В заключение отметим, что если периодическая функция  периода Т представлена рядом Фурье в комплексной форме: , то комплексные коэффициенты  будем называть совокупностью комплексных амплитуд ряда Фурье. Совокупность модулей комплексных коэффициентов Фурье и будет давать амплитудный спектр данной периодической функции. Если ввести обозначение = , то в силу того, что = , можно сделать вывод, что амплитудный спектр симметричен относительно оси ординат.

Вопросы для самопроверки

1. Что такое амплитудно-частотный ряд Фурье

2. Дайте определение  амплитудного спектра ряда Фурье в комплексной форме

⇐ Предыдущая12345Следующая ⇒

Поделиться: