Изменение удельной энтропии и температуры при дросселировании

Дросселирование является необратимым процессом, так как часть энергии потока теряется на его завихрение перед диафрагмой и за ней и преобразуется в теплоту, которая при адиабатном течении передается рабочему телу. Если представить процесс, идущий в обратном направлении (например, в трубе, изображенной на рис. 34, изменить направление течения газа на обратное), то он по-прежнему будет сопровождаться падением давления при протекании газа через дроссель. Изменение удельной энтропии газа:

,

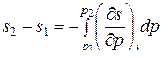его можно записать в виде: , .

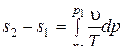Такая запись является наиболее удобной, так как 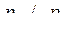. Из последнего уравнения следует, что всегда .

Для определения изменения температуры в процессе адиабатного дросселирования необходимо знать значение производной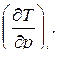  

Из соотношения 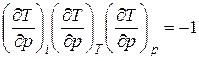 с учетом соотношений 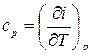,  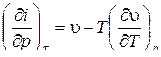получим .

Величина 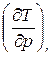 называется коэффициентом адиабатного дросселирования или дифференциальным дроссель-эффектом, его обозначают  В общем случае величина  отлична от нуля.

Явление изменения температуры газов и жидкостей при адиабатном дросселировании называется эффектом Джоуля – Томсона. Измеряя дифференциальный дроссель-эффект (весьма малую конечную разность температур 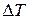 при такого же порядка разности давлений по обе стороны дросселя 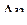), можно по результатам этих измерений найти величину , затем построить i, Т-диаграмму исследуемого вещества, определить удельную теплоемкость 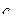, удельный объем и т. д.

Изменение температуры газа (жидкости) при значительном перепаде давлений на дросселе называется интегральным дроссель-эффектом, он вычисляется из соотношения

где 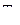,  – температуры дросселируемого вещества соответственно перед дросселем и за ним.

Интегральный дроссель-эффект может достигать весьма большой величины. Например, при дросселировании водяного пара от давления  и температуры 450 °С до давления, равного 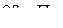, температура пара уменьшается до 180 °С, т. е. на 270 °С.

 

Рис. 35. i, Т-диаграмма

Определение величины интегрального адиабатного дроссель-эффекта удобно выполнять с помощью i, Т-диаграммы дросселируемого вещества (рис. 35). Если известно состояние газа перед дросселем, т. е. его давление  и температура , и известно давление за дросселем 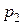, то, нанеся точку 1 и найдя точку пересечения изоэнтальпы i = const с изобарой , получим температуру за дросселем .

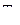Знак дроссель-эффекта

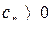Проанализируем соотношение . Поскольку всегда , то знак коэффициента определяется знаком стоящей в числителе правой части уравнения.

Очевидно, что если , то , и тогда температура дросселируемого вещества возрастает.

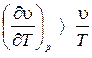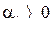Если , то , и тогда температура дросселируемого вещества уменьшается.

 

Если , то , и тогда температура дросселируемого вещества не меняется. Для идеального газа характерно 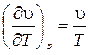, тогда идеальный газ дросселируется без изменения температуры.

 Таким образом, для газа, подчиняющегося уравнению Ван-дер-Ваальса, эффект Джоуля – Томсона не равен нулю.

Как показывает опыт, для одного и того же вещества  оказывается различным в зависимости от области состояния. Состояние газа (жидкости), в котором  равен нулю, называется точкой инверсии эффекта Джоуля – Томсона. Геометрическое место точек инверсии на диаграмме состояния данного вещества называется кривой инверсии. Точки на кривой инверсии удовлетворяют уравнению . Пользуясь этим условием, можно найти кривую инверсии с помощью уравнения состояния вещества.

 

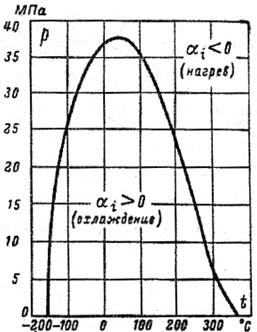Рис. 36. Кривая инверсии азота

В качестве примера на рис. 36 приведена кривая инверсии азота в p, t-диаграмме. Внутри области, ограниченной кривой инверсии , т. е. газ при дросселировании охлаждается. Вне этой области , т. е. температура газа при дросселировании повышается. Аналогичный характер имеют кривые инверсии других веществ. Процесс дросселирования используют для регулирования работы паросиловых установок, так как с увеличением дросселирования уменьшаются расход рабочего тела и располагаемая работа (теплоперепад). Действительно, если без дросселирования располагаемая работа равна  (рис. 37), то

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться: