Понятие стационарного случайного процесса

 

В отличие от числовых характеристик случайных величин, представляющих собой определённые числа, аналогичные характеристики случайных процессов в общем случае являются не числами, а функциями.

Математическим ожиданием случайного процесса  называется неслучайная функция , которая при каждом значении  равна математическому ожиданию соответствующего сечения, т.е. 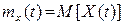. Математическое ожидание есть некоторая “средняя” функция, вокруг которой группируются возможные реализации этого случайного процесса.

Дисперсией случайного процесса  называется неслучайная функция , которая при каждом значении  равна дисперсии соответствующего сечения, т.е.

, где .

Дисперсия характеризует среднюю степень рассеивания (разброса) возможных реализаций случайного процесса относительно .

Автокорреляционной функцией случайного процесса  называется неслучайная функция двух аргументов , которая при каждой паре значений  равна корреляционному моменту соответствующих сечений, т.е.

, где , .

Автокорреляционная функция характеризует вероятностную зависимость между двумя произвольными сечениями случайного процесса.

Если сечения случайного процесса  являются непрерывными СВ, то математическое ожидание, дисперсия и автокорреляционная функция определяются по формулам

, ,

.

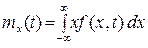Случайный процесс  называется стационарным, если при любых значениях  имеют место равенства  и , где 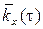 – некоторая функция одного неслучайного аргумента. Из второго равенства следует, что для стационарного случайного процесса 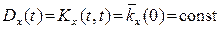. Таким образом, математическое ожидание и дисперсия стационарного случайного процесса не зависят от времени, а автокорреляционная функция зависит только от степени близости значений своих аргументов.

 

6.3. Дискретная цепь Маркова: основные понятия и свойства

 

Пусть  – последовательность случайных величин, элементы которой представляют собой дискретные СВ с возможными значениями из множества . Если при любом  для всех 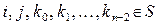 имеет место

,

то эта последовательность называется дискретной цепью Маркова. Элементы множества S будем называть состояниями цепи, а значение  – вероятностью перехода цепи из состояния i в состояние j на n-м шаге.

Дискретная цепь Маркова называется однородной, если её вероятности перехода  не зависят от номера шага n. Пусть , , 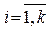 – вероятности перехода за один шаг, тогда матрица  называется матрицей перехода цепи за один шаг. Её элементы обладают свойствами:

1⁰. , , .

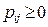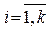2⁰. , .

Первое свойство вытекает из неотрицательности вероятностей, второе – из того, что события, состоящие в переходе цепи из любого фиксированного состояния i в различные состояния множества S, являются попарно несовместными и образуют полную группу.

Теорема 1. Для однородной цепи при любых  имеют место равенства , , .

Значения , ,  называются вероятностями перехода за m шагов, а матрица 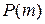, элементами которой являются вероятности  – матрицей перехода цепи за m шагов. Значения ,  будем называть начальными вероятностями состояний цепи.

Теорема 2. Справедливо равенство , .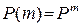

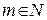Из теоремы 2 следует, что матрица Р однозначно определяет вероятности перехода за любое конечное число шагов. Поскольку события ,  попарно несовместны и образуют полную группу, то ,

а в силу формулы полной вероятности

, , .

Отсюда и из равенства 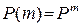 следует, что зная начальные вероятности ,  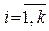и матрицу перехода Р, можно найти вероятность для любого состояния на любом шаге.

Теорема 3. Если при некотором 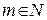 все элементы матрицы  строго положительны, то существуют пределы

, , .

Условие положительности элементов матрицы  означает, что за m шагов возможен переход цепи из каждого состояния в любое другое или в то же самое состояние с ненулевой вероятностью. Из теоремы 3 следует, что при определённом условии строки матрицы  для достаточно больших m практически совпадают между собой, т.е. вероятности состояний однородной цепи через большое число шагов почти перестают зависеть от начального состояния. Цепь Маркова, обладающая этим свойством, называется эргодической, а числа 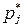,  называются финальными вероятностями состояний цепи.

Пусть  – попарно несовместные события, образующие полную группу. Будем считать, что эксперимент повторяется неограниченное число раз, причём вероятности событий  в n-м опыте зависят только от появления этих событий в ( )-м опыте и не зависят от их появления в предыдущих опытах. Если n – номер эксперимента (полагается 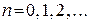), а  – номер события, наступившего в n-м эксперименте, то последовательность , получаемая в данной серии зависимых испытаний, представляет собой цепь Маркова.

⇐ Предыдущая1234

Поделиться: