Глава II . Одномерное уравнение переноса с переменными коэффициентами
Постановка задачи
Рассмотрим уравнение вида:


 (1)
(1)
удовлетворяющий начальным условиям
 (2)
(2)
и граничным условиям:

 (3)
(3)
Входные данные:
1) 
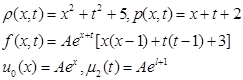 l=1, T=1
l=1, T=1
точное решение: 
2) 

точное решение: 
3) 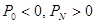

точное решение: 
4) 

точное решение: 
Для решения задачи (1) – (3) используем различные разностные схемы, вернее, явную и неявную.
Явные ” схемы
Явные схемы для нашей задачи используются тогда, когда p(x, t) > 0, (p0> 0, pN> 0) или p(x, t)< 0, (p0< 0, pN< 0). На практике часто используют схему бегущего счета. В зависимости от знака функции p(x, t) используют правую или левую разностные схемы.
Итак, рассмотрим схему бегущего счета в обоих случаях.
1) p(x, t)> 0, (p0> 0, pN> 0)
Разностная схема (правая) имеет вид
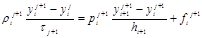 ; (1′ )
; (1′ )
 ; (2′ )
; (2′ )
 ; (3′ )
; (3′ )
из (1′ )  ,
,
где 

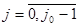 .
.
2) p(x, t)< 0, (p0< 0, pN< 0)
В этом случае используется левая разностная схема
 ; (1″ )
; (1″ )
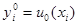 ; (2″ )
; (2″ )
 ; (3″ )
; (3″ )
из (1′ )  ,
,
где 
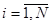
 .
.
Таблица 1 Численное решение уравнения переноса с переменными коэффициентами схема бегущего счета “явная ” схема (правая разностная схема)
| -------------kogda p0> 0, pN> 0-------------50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.10039200
| 0.10004559
| 0.00034641
|
| 1
| 0.10731313
| 0.10694264
| 0.00037049
|
| 2
| 0.11471141
| 0.11431517
| 0.00039623
|
| 3
| 0.12261970
| 0.12219596
| 0.00042375
|
| 4
| 0.13107319
| 0.13062004
| 0.00045315
|
| 5
| 0.14010945
| 0.13962487
| 0.00048458
|
| 6
| 0.14976865
| 0.14925048
| 0.00051817
|
| 7
| 0.16009374
| 0.15953968
| 0.00055407
|
| 8
| 0.17113063
| 0.17053820
| 0.00059243
|
| 9
| 0.18292837
| 0.18229495
| 0.00063342
|
| 10
| 0.19553941
| 0.19486220
| 0.00067721
|
| 11
| 0.20901984
| 0.20829583
| 0.00072401
|
| 12
| 0.22342957
| 0.22265555
| 0.00077402
|
| 13
| 0.23883258
| 0.23800523
| 0.00082736
|
| 14
| 0.25528740
| 0.25441310
| 0.00087431
|
| 15
| 0.27195211
| 0.27195211
| 0.00000000
|
Таблица 2. Численное решение уравнения переноса с переменными коэффициентами схема бегущего счета “явная ” схема (левая разностная схема)
| -------------kogda p0< 0, pN< 0-------------- 50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.14715178
| 0.14715178
| 0.00000000
|
| 1
| 0.14242453
| 0.14232757
| 0.00009697
|
| 2
| 0.13785337
| 0.13766151
| 0.00019185
|
| 3
| 0.13343317
| 0.13314843
| 0.00028474
|
| 4
| 0.12915902
| 0.12878331
| 0.00037571
|
| 5
| 0.12502613
| 0.12456129
| 0.00046484
|
| 6
| 0.12102988
| 0.12047768
| 0.00055219
|
| 7
| 0.11716580
| 0.11652796
| 0.00063785
|
| 8
| 0.11342959
| 0.11270772
| 0.00072187
|
| 9
| 0.10981705
| 0.10901272
| 0.00080434
|
| 10
| 0.10632415
| 0.10543886
| 0.00088530
|
| 11
| 0.10294698
| 0.10198216
| 0.00096483
|
| 12
| 0.09968176
| 0.09863879
| 0.00104298
|
| 13
| 0.09652483
| 0.09540502
| 0.00111981
|
| 14
| 0.09347266
| 0.09227727
| 0.00119539
|
| 15
| 0.09052183
| 0.08925206
| 0.00126976
|
Текст программы смотри в приложении 1
Неявные схемы
В отличие от явной схемы неявные схемы используются для задачи (1) – (3) во всех случаях 1) p0> 0, pN> 0; 2) p0< 0, pN< 0; 3) p0> 0, pN< 0; 4) p0< 0, pN> 0.
Рассмотрим 2 различные разностные схемы:
1) Центрально- разностная схема.
2) Трехточечная схема с весом.
Все эти схемы решаются методом прогонки и все эти разностные уравнения, т.е. полученные при аппроксимации схемы, вернее, уравнения сводятся к виду:

 (4)
(4)
Коэффициенты Ai, Bi, Ci должны удовлетворять условиям:
 (5)
(5)
Коэффициенты B0 , C0, F0, AN, CN, FN находятся из граничных условий. В данной задаче в зависимости от знака функции p(x, t) ставятся граничные условия и тем самым находятся наши коэффициенты. Рассмотрим все 4 случая:
1) p 0 > 0, pN > 0, u ( l, t )=м2( t ), (3′ )
из уравнения (3′ ) 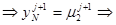 AN, CN, FN.
AN, CN, FN.
B0 , C0, F0 находятся из дополнительного условия, которая ставится на левом конце.
2) p 0 < 0, pN < 0, u (0, t )=м1( t ), (3″ )из уравнения (3″ ) 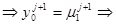 B0 , C0, F0.
B0 , C0, F0.
AN, CN, FN находятся из дополнительного условия, которая ставится на правом конце.
3) p 0 < 0, pN > 0, u (0, t )=м1( t ), u ( l, t )=м2( t ), (3″ ′ )
из уравненя (3″ ′ ) 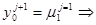 B0 , C0, F0
B0 , C0, F0
 AN, CN, FN
AN, CN, FN
4) p 0 > 0, pN < 0, нет граничных условий.
Дополнительное условие ставится на левом и на правом концах. Находим B0, C0, F0 , AN, CN, FN.
Алгоритм правой прогонки

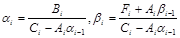 ,
,  .
.
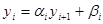 ,
, 
 .
.
При выполнении условий 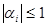 алгоритм правой прогонки устойчив.
алгоритм правой прогонки устойчив.
Центрально разностная схема
Разностная схема имеет вид (задачи (1)-(3)):
 ,
,  .
.


1) P0> 0, PN> 0

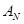 ,
,  ,
,  .
.

2) P0< 0, PN< 0

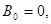

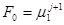 .
.

3) P0< 0, PN> 0
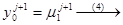 B0=0, C0=1, F0=
B0=0, C0=1, F0=  ,
,
 → AN=0, CN=1,
→ AN=0, CN=1,  .
.
4) P0> 0, PN< 0

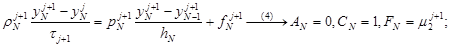


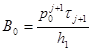 ,
, 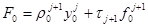



Таблица 3. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0> 0, pN> 0------------ 50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.18772094
| 0.18765555
| 0.00006539
|
| 1
| 0.18147920
| 0.18150347
| 0.00002427
|
| 2
| 0.17566576
| 0.17555308
| 0.00011268
|
| 3
| 0.16982701
| 0.16979776
| 0.00002924
|
| 4
| 0.16440069
| 0.16423113
| 0.00016956
|
| 5
| 0.15890974
| 0.15884699
| 0.00006275
|
| 6
| 0.15384782
| 0.15363937
| 0.00020845
|
| 7
| 0.14868453
| 0.14860247
| 0.00008206
|
| 8
| 0.14391438
| 0.14373070
| 0.00018368
|
| 9
| 0.13904086
| 0.13901865
| 0.00002221
|
| 10
| 0.13462315
| 0.13446108
| 0.00016208
|
| 11
| 0.13004378
| 0.13005292
| 0.00000914
|
| 12
| 0.12593278
| 0.12578928
| 0.00014351
|
| 13
| 0.12169429
| 0.12166541
| 0.00002888
|
| 14
| 0.11786577
| 0.11767675
| 0.00018903
|
| 15
| 0.11381884
| 0.11381884
| 0.00000000
|
Таблица 4. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0< 0, pN< 0-------------- 50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.14715178
| 0.14715178
| 0.00000000
|
| 1
| 0.14240331
| 0.14232757
| 0.00007574
|
| 2
| 0.13769681
| 0.13766151
| 0.00003530
|
| 3
| 0.13325746
| 0.13314843
| 0.00010903
|
| 4
| 0.12885248
| 0.12878331
| 0.00006918
|
| 5
| 0.12470227
| 0.12456129
| 0.00014098
|
| 6
| 0.12057943
| 0.12047768
| 0.00010174
|
| 7
| 0.11669966
| 0.11652796
| 0.00017170
|
| 8
| 0.11284082
| 0.11270772
| 0.00013310
|
| 9
| 0.10921401
| 0.10901272
| 0.00020130
|
| 10
| 0.10560221
| 0.10543886
| 0.00016335
|
| 11
| 0.10221201
| 0.10198216
| 0.00022985
|
| 12
| 0.09883137
| 0.09863879
| 0.00019259
|
| 13
| 0.09566248
| 0.09540502
| 0.00025746
|
| 14
| 0.09249816
| 0.09227727
| 0.00022089
|
| 15
| 0.08953626
| 0.08925206
| 0.00028420
|
Таблица 5. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0< 0, pN> 0--------------50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.03678794
| 0.03678794
| 0.00000000
|
| 1
| 0.03565917
| 0.03558189
| 0.00007728
|
| 2
| 0.03439784
| 0.03441538
| 0.00001754
|
| 3
| 0.03335557
| 0.03328711
| 0.00006846
|
| 4
| 0.03216179
| 0.03219583
| 0.00003404
|
| 5
| 0.03119895
| 0.03114032
| 0.00005863
|
| 6
| 0.03007027
| 0.03011942
| 0.00004915
|
| 7
| 0.02917987
| 0.02913199
| 0.00004788
|
| 8
| 0.02811435
| 0.02817693
| 0.00006258
|
| 9
| 0.02728957
| 0.02725318
| 0.00003639
|
| 10
| 0.02628567
| 0.02635971
| 0.00007405
|
| 11
| 0.02551993
| 0.02549554
| 0.00002439
|
| 12
| 0.02457633
| 0.02465970
| 0.00008337
|
| 13
| 0.02386341
| 0.02385126
| 0.00001215
|
| 14
| 0.02297890
| 0.02306932
| 0.00009042
|
| 15
| 0.02231302
| 0.02231302
| 0.00000000
|
Таблица 6. Численное решение уравнения переноса с переменными коэффициентами центральная разностная схема метод прогонки
| -------------kogda p0> 0, pN< 0--------------50sloy
|
| N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.00379722
| 0.00375311
| 0.00004410
|
| 1
| 0.00328998
| 0.00328462
| 0.00000536
|
| 2
| 0.00291427
| 0.00287461
| 0.00003966
|
| 3
| 0.00250378
| 0.00251579
| 0.00001200
|
| 4
| 0.00225176
| 0.00220175
| 0.00005001
|
| 5
| 0.00190450
| 0.00192691
| 0.00002241
|
| 6
| 0.00172045
| 0.00168638
| 0.00003407
|
| 7
| 0.00145947
| 0.00147588
| 0.00001640
|
| 8
| 0.00129005
| 0.00129165
| 0.00000159
|
| 9
| 0.00109247
| 0.00113042
| 0.00003795
|
| 10
| 0.00092289
| 0.00098931
| 0.00006642
|
| 11
| 0.00074314
| 0.00086582
| 0.00012268
|
| 12
| 0.00056520
| 0.00075774
| 0.00019254
|
| 13
| 0.00038370
| 0.00066315
| 0.00027946
|
| 14
| 0.00020306
| 0.00058037
| 0.00037731
|
| 15
| 0.00002275
| 0.00050793
| 0.00048518
|
Текст программы смотри в приложении 2
Трехточечная схема с весом
Разностная схема для нашей задачи ((1)-(3)) имеет вид:
 (0)
(0)
Уравнение (0) приведем к виду
 (1)
(1)
Из уравнения (1) находим коэффициенты 


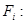
 ,
, 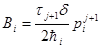 ,
,  ,
,
 .
.
1) P0> 0, PN> 0 yNj+1 = м2j+1 → AN =0, CN=1, FN = м2j+1
 (1.0)
(1.0)
Уравнение (1.0) приводим к виду
 (1.1)
(1.1)
Из уравнения (1.1) находим 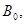


 ,
, 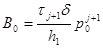 ,
,
 .
.
2) P 0 < 0, PN < 0 y0j+1 = м1j+1 → B 0 =0, C 0 =1, F 0 = м1 j +1
 . (2.0)
. (2.0)
Уравнение (2.0) приводим к виду
 (2.1)
(2.1)
Из уравнения (2.1) находим 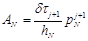 ,
,  ,
,
 .
.
3) P 0 < 0, PN > 0
y0j+1 = м1j+1 → B 0 =0, C 0 =1, F 0 = м1 j +1 ,
yNj+1 = м2j+1 → AN=0, CN=1, FN= м2j+1.
4) P0> 0, PN< 0

B0 =0, C0=1, F0= м1j+1

AN =0, CN =1, FN = м2 j +1
Таблица 7. Численное решение уравнения переноса с переменными коэффициентами Трехточечная схема с весом Метод прогонки
| -------------------kogda p0> 0, pN> 0---------------kogda G=1
|
| 50sloy N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.36842774
| 0.36787944
| 0.00054830
|
| 1
| 0.35627966
| 0.35581892
| 0.00046075
|
| 2
| 0.34461653
| 0.34415379
| 0.00046275
|
| 3
| 0.33324870
| 0.33287108
| 0.00037762
|
| 4
| 0.32234219
| 0.32195827
| 0.00038392
|
| 5
| 0.31170418
| 0.31140322
| 0.00030095
|
| 6
| 0.30150555
| 0.30119421
| 0.00031134
|
| 7
| 0.29155019
| 0.29131989
| 0.00023030
|
| 8
| 0.28201389
| 0.28176929
| 0.00024460
|
| 9
| 0.27269705
| 0.27253179
| 0.00016526
|
| 10
| 0.26378042
| 0.26359714
| 0.00018329
|
| 11
| 0.25506082
| 0.25495540
| 0.00010543
|
| 12
| 0.24672399
| 0.24659696
| 0.00012703
|
| 13
| 0.23856301
| 0.23851255
| 0.00005045
|
| 14
| 0.23076867
| 0.23069318
| 0.00007549
|
| 15
| 0.22313016
| 0.22313016
| 0.00000000
|
Таблица 8. Численное решение уравнения переноса на с переменнми коэффициентами Трехточечная схема с весом Метод прогонки
| -------------------kogda p0> 0, pN> 0---------------kogda G=0.5
|
| 50sloy N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.22317966
| 0.36787944
| 0.14469979
|
| 1
| 0.32550240
| 0.35581892
| 0.03031652
|
| 2
| 0.21980791
| 0.34415379
| 0.12434588
|
| 3
| 0.32390953
| 0.33287108
| 0.00896156
|
| 4
| 0.17318247
| 0.32195827
| 0.14877580
|
| 5
| 0.30172608
| 0.31140322
| 0.00967714
|
| 6
| 0.15878469
| 0.30119421
| 0.14240953
|
| 7
| 0.28118803
| 0.29131989
| 0.01013186
|
| 8
| 0.16595060
| 0.28176929
| 0.11581869
|
| 9
| 0.25958363
| 0.27253179
| 0.01294816
|
| 10
| 0.10012442
| 0.26359714
| 0.16347272
|
| 11
| 0.23108668
| 0.25495540
| 0.02386872
|
| 12
| 0.10648083
| 0.24659696
| 0.14011613
|
| 13
| 0.24403326
| 0.23851255
| 0.00552071
|
| 14
| 0.10163574
| 0.23069318
| 0.12905744
|
| 15
| 0.22313016
| 0.22313016
| 0.00000000
|
Таблица 9. Численное решение уравнения переноса с переменными коэффициентами Трехточечная схема с весом Метод прогонки
| -------------------kogda p0< 0, pN< 0--------------- kogda G=1
|
| 50sloy N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.36787944
| 0.36787944
| 0.00000000
|
| 1
| 0.35801340
| 0.35581892
| 0.00219448
|
| 2
| 0.36845033
| 0.34415379
| 0.02429654
|
| 3
| 0.35906842
| 0.33287108
| 0.02619734
|
| 4
| 0.37000945
| 0.32195827
| 0.04805117
|
| 5
| 0.36101823
| 0.31140322
| 0.04961501
|
| 6
| 0.37246014
| 0.30119421
| 0.07126592
|
| 7
| 0.36379087
| 0.29131989
| 0.07247098
|
| 8
| 0.37571304
| 0.28176929
| 0.09394375
|
| 9
| 0.36731988
| 0.27253179
| 0.09478809
|
| 10
| 0.37968642
| 0.26359714
| 0.11608928
|
| 11
| 0.37154421
| 0.25495540
| 0.11658881
|
| 12
| 0.38430710
| 0.24659696
| 0.13771013
|
| 13
| 0.37640856
| 0.23851255
| 0.13789601
|
| 14
| 0.38951172
| 0.23069318
| 0.15881854
|
| 15
| 0.38186439
| 0.22313016
| 0.15873423
|
Таблица 10 Численное решение уравнения переноса с переменными коэффициентами Трехточечная схема с весом Метод прогонки
| -------------------kogda p0< 0, pN< 0---------------
|
| kogda G=0, 5 50sloy N priblijennoe tochnoe pogreshnosti
|
| 0
| 0.36787944
| 0.36787944
| 0.00000000
|
| 1
| 0.31801913
| 0.35581892
| 0.03779978
|
| 2
| 0.36478621
| 0.34415379
| 0.02063242
|
| 3
| 0.34573407
| 0.33287108
| 0.01286299
|
| 4
| 0.36983022
| 0.32195827
| 0.04787195
|
| 5
| 0.36678412
| 0.31140322
| 0.05538090
|
| 6
| 0.34570117
| 0.30119421
| 0.04450696
|
| 7
| 0.34004986
| 0.29131989
| 0.04872997
|
| 8
| 0.33360167
| 0.28176929
| 0.05183238
|
| 9
| 0.35119193
| 0.27253179
| 0.07866014
|
| 10
| 0.35046403
| 0.26359714
| 0.08686690
|
| 11
| 0.35792253
| 0.25495540
| 0.10296714
|
| 12
| 0.36451445
| 0.24659696
| 0.11791748
|
| 13
| 0.35527614
| 0.23851255
| 0.11676359
|
| 14
| 0.38271932
| 0.23069318
| 0.15202614
|
| 15
| 0.39593489
| 0.22313016
| 0.17280473
|
Текст программы смотри в приложении 3

