| Обоснование и выбор конкретных управленческих решений, связанных с финансовыми рисками, базируется на концепции и методологии " теории принятия решений". Эта теория предполагает, что решениям, связанным с риском, всегда свойственны элементы неизвестности конкретного поведения исходных параметров, которые не позволяют четко детерминировать значения конечных результатов этих решений. В азвисимости от степени неизвестности предстоящего поведения исходных параметров принятия решений различают " условия риска", в которых вероятность наступления отдельных событий, влияющих на конечный результат, может быть установлена с той или иной степенью точности, и условия неопределенности, в которых из-за отсутствия необходимой информации такая вероятность не может быть установлена.
Теория принятия решений в условиях риска и неопределенности основывается на следующих исходных положениях:
Объект принятия решения четко детерминирован и по нему известны основные из возможных факторов риска. В финансовом менеджменте такими объектами выступают отдельная финансовая операция, конкретный вид ценных бумаг, группа взаимоисключающих реальных инвестиционных проектов и т.п.
По объекту принятия решения избран показатель, который наилучшим образом характеризует эффективность этого решения. По краткосрочным финансовым операциям таким показателем избирается обычно сумма или уровень чистой прибыли, а по долгосрочным — чистый приведенный доход или внутренняя ставка доходности.
По объекту принятия решения избран показатель, характеризующий уровень его риска. Финансовый риски характеризуются обычно степенью возможного отклонения ожидаемого показателя эффективности (чистой прибыли, чистого приведенного дохода и т.п.) от средней или ожидаемой его величины. Имеется конечное количество альтернатив принятия решения (конечное количество альтернативных реальных ин-вестиционных проектов, конкретных ценных бумаг, способов осуществления определенной финансовой операции и т.п.).
Имееется конечное число ситуаций развития собы-тия под влиянием изменения факторов риска. В финансовом менеджменте каждая из таких ситуаций характеризует одно из возможных предстоящих состояний внешней финансовой среды под влиянием изменений отдельных факторов риска. Число таких ситуаций в процессе принятия решений должно быть детерминировано в диапазоне от крайне благопри-ятных (наиболее оптимистическая ситуация) до крайне неблагоприятных (наиболее пессимистическая ситуация).
По каждому сочетанию альтернатив принятия ре-шений и ситуаций развития события может быть определен конечный показатель эффективности решения (конкретное значение суммы чистой прибыли, чистою приведенного дохода и т.п., соответствующее данному сочетанию).
По каждой из рассматриваемой ситуации возможна или невозможна оценка вероятности ее реализации. Возможность осуществления оценки вероятности разделяет всю систему принимаемых рисковых решений на ранее рас-смотренные условия их обоснования (" условия риска" или " условия неопределенности51).
Выбор решения осуществляется по наилучшей из рас-сматриваемых альтернатив.
Методология теории принятия решения в условиях рис-ка и неопределенности предполагает построение в процессе обоснования рисковых решений так называемой " матри-цы решений", которая имеет следующий вид (табл. 4.8):

Таблица 4.8
„Матрица решений", выстраиваемая в процессе принятия решения в условиях риска
или неопределенности
В приведенной матрице значения А|; А2; ... Ап харак-теризуют каждый из вариантов альтернатив принятия ре-шения; значения С]; С2; ...; Сп — каждый из возможных вариантов ситуации развития событий; значения 3ц; Э12; Э1п; Э21; Э22; Э2п; Эпи Эп2; ...; Эпп — конкретный уровень эффективности решения, соответствующий опреде-ленной альтернативе при определенной ситуации.
Приведенная матрица решений характеризует один из ее видов, обозначаемый как " матрица выигрышейтак как она рассматривает показатель эффективности. Возможно построение матрицы решений и другого вида, обозначае-мого как " матрица рисков " в котором вместо показателя эффективности используется показатель финансовых по-терь, соответствующих определенным сочетаниям альтер-натив принятия решений и возможным ситуациям разви-тия событий.
На основе указанной матрицы рассчитываетсся наи-лучшее из альтернативных решений по избранному крите-рию. Методика этого расчета дифференцируется для усло-вий риска и условий неопределенности.
I. Принятие решений в условиях риска основано на том, что каждой возможной ситуации развития событий может быть задана определенная вероятность его осущест-вления. Это позволяет взвесить каждое из конкретных зна-чений эффективности по отдельным альтернативам на значение вероятности и получить на этой основе инте-гральный показатель уровня риска, соответствующий каждой из альтернатив принятия решений. Сравнение этого интегрального показателя по отдельным альтернативам позволяет избрать для реализации ту из них, которая приводит к избранной цели (заданному показателю эффектив-ности) с наименьшим уровнем риска.
Оценка вероятности реализации отдельных ситуаций развития событий может быть получена экспертным путем.
В рамках каждой из альтернатив принятия решений отдельные значения эффективности с учетом их верятности рассматриваются как случайные переменные, подчиняющи-еся определенному закону распределения вероятностей. Рас-пределение вероятностей представляет собой набор значе-ний, которые может принимать случайная переменная (в нашем случае — эффективность решений) при соответству-ющей вероятности возможных ситуаций развития событий.
Для большинства финансовых операций характерно нормальное распределение вероятностей (распределение Гаусса), хотя в практике оценки риска отдельных реаль-ных инвестиционных проектов могут использоваться и другие их виды (распределение Лапласа, распределение Стыодента, треугольное распределение). График нормаль-ного распределения представлен на рис. 4.15.

Рисунок 4.15. График нормального распределения вероятности.
При построении матрицы решений с учетом вероят-ности реализации отдельных ситуаций могут быть исполь-зованы методы анализа сценариев, иммитационного моде-лирования, дерева решений и другие (подробно каждый из этих методов рассматривается в третьем томе Энциклопе-дии на примере оценки рисков отдельных реальных инве-стиционных проектов).
Исходя из матрицы решений, построенной в услови-ях риска с учетом вероятности реализации отдельных си-туаций, рассчитывается интегральный уровень риска по каждой из альтернатив принятия решений. При его расчете используются следующие основные показатели:
179? среднеквадратическое (стандартное) отклонение.
коэффициент вариации.
Для отдельных видов финансовых операций кроме вышеперечисленных для оценки рисков могут применяться также показатели коэффициента корреляции, коэффициента " бета" и другие.
В процессе рассмотрения интегральных значений уровня риска по каждой из альтернатив принятия решения, предпочтение отдается той, по которой уровень риска имеет наименьшее значение (при прочих равных условиях).
Рассмотренный подход к принятию решений в усло-виях риска позволяет получить объективные вероятностные результаты оценки их эффективности. Однако этот подход не учитывает того факта, что каждый из субъектов, принимающих рисковые финансовые решения, исходит из своих субъективных рисковых предпочтений (т.е. из своего субъективного отношения к риску — неприятия риска, нейтральности к риску или склонности к риску). Графически субъективные рисковые предпочтения лиц, принимающих решения, характеризуются " кривыми безразли-чия", представленными на рис. 4.16.
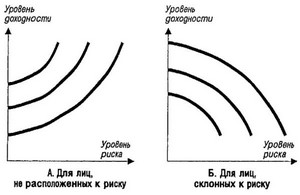
Рисунок 4.17. График „кривых безразличия" для лиц, не распо-ложенных и склонных к риску.
Как видно из приведенного графика, для лиц, не расположенных к риску (вариант " А" ), функции " кривых безраз-личия" являются возрастающими по отношению к уровню доходности и убывающими по отношению к уровню риска. Соотвественно, для лиц, расположенных к риску, функции " кривых безразличия" носят противоположный характер — они являются возрастающими по отношению к уровню риска и убывающими по отношению к уровню доходности.
В основе выбора рисковых финансовых решений с учетом рисковых предпочтений инвестора лежит" принцип Бсрнулли", в соотвествии с которым лицо, принимающее решение, связывает " полезность" этого решения со своим субъективным 01 ношением к риску. На основе этого принципа Дж. Нейманом и О. Монгерштерном была разработана в 1944 году оля практического пользования специальная модель принятия рисковых решений, получивших название " функция полезности Неймана—Монгерштерна В современной модификации эта модель принятия рисковых решений основывается на следующих шести аксиомах:
Аксиома сравнимости. Она состоит в том, что из всех рассматриваемых альтернатив принятия решений субъект оценки исходит из того, что с учетом его личных рисковых предпочтений результат оценки Э1 для него предпочтительней в сравнении с результатом Э2:
Э1? Э2
Аксиома транзитивности. Она состоит в том, что если для субъекта, принимающего решение с учетом рискового предпочтения, результат оценки Э^ предпочтительней результатат Э2, а последний предпочтительней, чем ре- зульгат Э3, то результат оценки Э] автоматически будет предпочтителен результату Э3:

Аксиома измеримости. Она состоит в том, что если для субъекта, принимающего решение, существует ряд результатов Э(> Э2> Эз, то существует вероятность Р (при 0< Р< 1), при которой
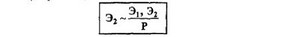

• Аксиома ограничения.
Она состоит в том, что для любого лица, принимающего решение с учетом рискового предпочтения, всегда существует самый большой (максимальный) и самый маленький (минимальный) результат оценки, в рамках которого он осуществляет свой выбор:

• Аксиома доминирования. Она состоит в том, что если две ситуации дают одинаковый результат с учетом рискового предпочтения лица, принимающего решение, то выбор осуществляется в пользу ситуации, имеющей большую вероятность:

• Аксиома независимости. Она состоит в том, что если лицо, принимающее решение, оценивает один из результатов как более предпочтительный и с учетом своих рисковых предпочтений, то выбор делается в пользу такой альтернативы, независимо от вероятности получения этого результата:

С учетом приведенных аксиом, основу " функции полезности Неймана-Монгерштерна" составляет вывод о том, что субъект, принимающий решение исходя из своих рисковых предпочтений, всегда будет стремиться к максимизации ожидаемой полезности, т.е. из всех альтернатив принятия решения он выберет ту, которая обеспечивает наибольшую ожидаемую им полезность. Выбор рисковых решений на основе " функции полез-ности Неймана—Монгерштерна" осуществляется на осно ве специальной компьютерной программы по следующим этапам:
На первом этапе выбирается вид функции полезности, соответствующий рисковым предпочтениям лица, принимающего решения. Программа содержит три вида таких функций: для субъектов, не склонных к риску; для субъектов, нейтральных к риску; для субъектов, склонных к риску
Типы функций полезности Неймана-Монгерштерна, соответствующих различным рисковым предпочтениям субъектов, принимающих рисковые решения, графически представлены на рис. 4 17.
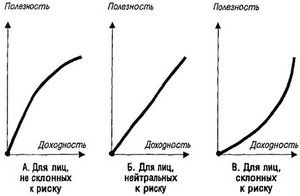
Рисунок 4.17. Графическое представление функций полезности
Неймана-Монгерштерна для лиц с различными рисковыми предпочтениями.
На втором этапе " матрица решений" (рассмотренная нами ранее) трансформируется в " матрицу полезности". В этих целях на основе заданной функции полезности каждый результат эффективности получает количественную оценку полезности (П1). " Матрица полезности", трансформирования из " матрицы решений", приобретает следующий вид (табл. 4.9):

Каждая из альтернатив принятия решений в этом слу чае может быть представлена в следующем виде;

На третьем этапе рассчитываются значения предпочтений каждой из альтернатив принятия решений как ожидаемых величин соответствующих распределений вероятности полезностей:
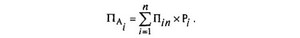
На четвертом этапе из всех рассчетных значений выбирается альтернатива принятия решения с максимально ожидаемой полезностью для субъкта с конкретным видом рискового предпочтения. Исходя из теории Неймана- Монгерштерна, максимально ожидаемая полезность характеризует оптимальную альтернативу принятия решений с учетом рискового предпочтения.
II, Принятие решений в условиях неопределенности ос-новано на том, что вероятности различных вариантов си-туаций развитии событий субъекту, принимающему рисковое решение, неизвестны. В этом случае при выборе альтернативы принимаемого решения субъект руководству-ется, с одной стороны, своим рисковым предпочтением, а с другой, — соответствующим критерием выбора из всех альтернатив по составленной им " матрице решений".
Основные критерии, используемые в процессе принятия решений о условиях неопределенности, представлены на рис. 4.18.

Рисунок 4.18. Система основных критериев, используемых в процессе принятия рисковых решений в условиях неопределенности.
Критерий Вальда (или критерий " максимина" ) предполагает, что из всех возможных вариантов " матрицы решений" выбирается та альтернатива, которая из всех самых неблагоприятных ситуаций развития события (минимизирующих значение эффективности) имеет наибольшее из минимальных значений (т.е. значение эффективности, лучшее из всех худших или максимальное из всех минимальных). Пример выбора альтернативы рискового решения по этому критерию приведен в табл. 4.10.
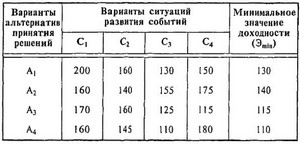
Таблица 4.10 Выбор оптимального рискового решения по критерию Вальда (критерию „максимина" ) на основе „матрицы решений"
Как видно из приведенной таблицы, оптимальная альтернатива рискового решения в условиях неопределенности по критерию Вальда (критерию " максимина" ) находится в затененном поле и соответствует 140 усл. ден. ед. (это значение эффективности является максимальным из всех минимальных ее значений при наихудших вариантах ситуаций).
Критерием Вальда (критерием " максимина" ) руководствуется при выборе рисковых решений в условиях неопределенности, как правило, субъект, не склонный к риску или рассматривающий возможные ситуации как пессимист.
Критерий " максимакса" предполагает, что из всех воз-можных вариантов " матрицы решений" выбирается та аль-тернатива, которая из всех самых благоприятных ситуаций развития событий (максимизирующих значение эффек-тивности) имеет наибольшее из максимальных значений (т.е. значение эффективности лучшее из всех лучших или максимальное из максимальных). Пример выбора альтер-нативы рискового решения по этому критерию приведен в табл. 4.11.
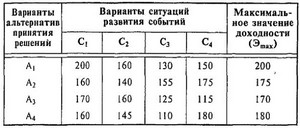
Таблица 4.11
Выбор оптимального рискового решения по критерию „максимакса" на основе „матрицы решений"
Из приведенной таблицы видно, что оптимальная альтернатива рискового решения в условиях неопределенности по критерию " максимакса", находящаяся в затененном
поле, соответствует 200 усл. ден. ед. (это значение эффективности является максимальным из всех максимальных ее значений при наилучших вариантах ситуаций).
Критерий " максимакса" используют при выборе рисковых решений в условиях неопределенности, как правило, субъекты, склонные к риску, или рассматривающие возможные ситуации как оптимисты.
Критерий Гурвица (критерий " оптимизма-пессимизма" или " альфа-критерий" ) позволяет руководствоваться при выборе рискового решения в условиях неопределенности некоторым средним результатом эффективности, находящимся в поле между значениями по критериям " максимакса" и " максимина" (поле между этими значениями связано посредством выпуклой линейной функции). Оптимальная альтернатива решения по критерию Гурвица определяется на основе следующей формулы:


Пример выбора альтернативы рискового решения по критерию Гурвица со значением " альфа-коэффициента", равным 0, 5 приведен в табл. 4.12.

Таблица 4.12
Выбор оптимального рискового решения
по критерию Гурвица на основе ранее рассмотренных „матриц решений"
Как видно из приведенной таблицы, оптимальная альтернатива рискового решения по критерию Гурвица, находится в затененном поле. Его средневзвешенная эффективность составляет 165 усл. ден. ед. Это значение эффективности является наибольшим среди всех средних ее значений, взвешенных по альфа-коэффициенту.
Критерий Гурвица используют при выборе рисковых решений в условиях неопределенности те субъекты, которые хотят максимально точно идентифицировать степень своих конкретных рисковых предпочтений путем задания значения альфа-коэффициента.
Критерий Сэвиджа (критерий потерь от " минимакса" ) предполагает, что из всех возможных вариантов " матрицы решений" выбирается та альтернатива, которая миними-зирует размеры максимальных потерь по каждому из воз-можных решений. При использовании этого критерия " матрица решения" преобразуется в " матрицу потерь" (один из вариантов " матрицы риска" ), в которой вместо значении эффективности проставляются размеры потерь при различных вариантах развития событий. Пример выбора альтернативы рискового решения по критерию Сэвиджа (критерию потерь от " минимакса" ) приведен в табл. 4.13.
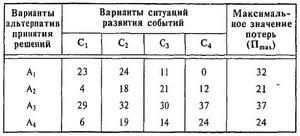
Таблица 4.13
Выбор оптимального рискового решения по критерию Сэвиджа на основе „матрицы потерь''
Из приведенной таблицы видно, что альтернатива рискового решения в условиях неопределенности по критерию Сэвиджа, находящаяся в затененном поле, имеет значение потерь, равное 21 усл. ден. ед. Это значение является наименьшим из всех максимальных значений потерь по каждой альтернативе при наихудшем варианте ситуаций развития событий.
Критерий Сэвиджа используется при выборе рисковых решений в условиях неопределенности, как правило, субъектами, не склонными к риску.
Рассмотренные методы принятия рисковых решений в условиях риска и неопределенности являются наиболее типичными и не охватывают все их многообразие, используемое в современном риск-менеджменте. В специальной литературе излагаются и другие более сложные методы оценки риска при решении конкретных задач.
Выше был рассмотрен методический инструментарий вычислений, наиболее широко используемый в современной практике финансового риск-менеджмента. Методический инструментарий расчетов отдельных специальных показателей рассматривается в последующих разделах книги.
|

