
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Действия с рациональными дробями
сложение и вычитание: или умножение и деление:
полезно помнить, что:
| |||||||||||||||||||||||||||||||
Функция 
| |||||||||||||||||||||||||||||||
| Квадратные уравнения формула корней квадратного уравнения:
пр: теорема Виета: разложение на множители:
метод выделения полного квадрата:
биквадратные уравнения: решают заменой переменной | |||||||||||||||||||||||||||||||
Дробно-рациональные уравнения
приводятся к виду:
 пр:
пр: 




| |||||||||||||||||||||||||||||||
Множества
множество - «набор элементов»
 - элемент a принадлежит множеству A - элемент a принадлежит множеству A
 - множество A принадлежит множеству B
пересечение множеств - множество A принадлежит множеству B
пересечение множеств  - множество элементов, принадлежащих обоим множествам (A и B)
объединение множеств - множество элементов, принадлежащих обоим множествам (A и B)
объединение множеств  - множество элементов, принадлежащих хотя бы одному из этих множеств (A или B)
пр: К - множество точек круга
Т - множество точек треугольника - множество элементов, принадлежащих хотя бы одному из этих множеств (A или B)
пр: К - множество точек круга
Т - множество точек треугольника
пр: множество целых чисел от 0 до 3 (конечное)
пр: множество четных чисел (бесконечное)
основные числовые множества: N - натуральные числа Z - целые числа Q - рациональные числа I - иррациональные числа (не рациональные, бесконечные непериодические десятичные дроби ) пр: R - действительные (вещественные) числа ( все точки числовой оси, от С - комплексные (мнимые) числа (
числовой промежуток - множество точек числовой оси:
| Неравенства
неравенство - отношение величин, записанное с одним из знаков:
 или или  «строгое» неравенство «строгое» неравенство
 или или  «не строгое» неравенство «не строгое» неравенство
 (не равно)
меньше то число, которое на числовой оси находится левее пр: (не равно)
меньше то число, которое на числовой оси находится левее пр: 
 - если
- если  и и 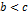 , то , то 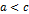 - если
- если  и и  , то , то 
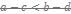  и и  , то , то 
  - если
- если  , то при , то при   при
при 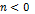  пр:
пр:  - если
- если  , то , то 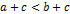
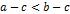 к левой и правой части неравенства можно прибавить (или отнять) одно число; т.е. можно перенести слагаемое из одной части неравенства в другую, изменив знак действия
пр:
к левой и правой части неравенства можно прибавить (или отнять) одно число; т.е. можно перенести слагаемое из одной части неравенства в другую, изменив знак действия
пр: 
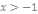 - если
- если  , то при , то при  при при 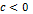 
 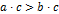
  обе части неравенства можно умножить (или разделить) на положительное число, но при умножении (или делении) на отрицательное число, нужно изменить знак неравенства
обе части неравенства можно умножить (или разделить) на положительное число, но при умножении (или делении) на отрицательное число, нужно изменить знак неравенства
решение неравенства - множество значений переменной, при которых неравенство верно решение системы неравенств - множество значений переменной, при которых все неравенства системы верны (т.е. пересечение множеств решений этих неравенств) решение неравенств (ответ) принято записывать в виде числовых промежутков пр:
| ||||||||||||||||||||||||||||||
Степень с целым показателем
Стандартный вид числа:
пр: | Функция
| ||||||||||||||||||||||||||||||
Погрешность приближения
абсолютная погрешность - модуль разности истинного и приближенного значений
относительная погрешность - отношение абсолютной погрешности к модулю истинного или приближенного значения
пр:  абс. погр.
абс. погр.  отн. погр.
отн. погр.  пр:
пр: 
| |||||||||||||||||||||||||||||||
алгебраическое выражение - конструкция из чисел и букв («переменных»), соединенных скобками и знаками арифметических действий  ОДЗ - область допустимых значений - значения переменных, при которых выражение имеет смысл
ОДЗ - область допустимых значений - значения переменных, при которых выражение имеет смысл
|
| ||||||||||||||||||||||||||||||
| пр: найти ОДЗ выражения | |||||||||||||||||||||||||||||||
| Уравнения n -ой степени | |||||||||||||||||||||||||||||||
| · если
· если пр: попробуем найти целый корень:
| · если  рациональный корень многочлена с целыми коэф-ми, то рациональный корень многочлена с целыми коэф-ми, то 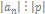 и и  и если
и если  , то , то  пр: рац.корни ур-я
пр: рац.корни ур-я  следует искать среди чисел: следует искать среди чисел:  при всех
при всех 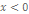  отриц. корней нет
возьмем отриц. корней нет
возьмем  должны выпол-ся условия должны выпол-ся условия  , ,  т.е. подходит только
т.е. подходит только  (но нужно проверить) (но нужно проверить)
| ||||||||||||||||||||||||||||||
Теорема Виета для уравнений n -ой степени




| |||||||||||||||||||||||||||||||
Алгебра - 9 класс
| Функция нули функции (точки пересечения с осью x ) - корни квадратного уравнения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
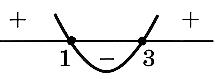
Квадратные неравенства

- решить квадратное уравнение
- схематично изобразить параболу - корни, направление ветвей
- выписать нужные промежутки
| пр: | 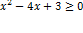

| 
|
|
| ||
| пр: | 
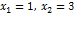

| 
|
| пр: | 


| 
|
| пр: | 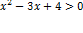
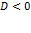

| 
|

| прямая | ||
|
| гипербола | ||
|
| парабола | ||
|
| окружность радиуса r c центром в точке (x0; y0) | ||
| пр: | 
| | |
Функция  (модуль)
(модуль)
|
| решение уравнений и неравенств с модулем:
 рассмотреть две ветви
рассмотреть две ветви
|

|
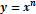 (степенная)
(степенная)

| 
|
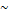 подсчет количества комбинаций
комбинаторное правило умножения - если нужно выбрать k элементов из некоторого множества элементов, и 1-ый элемент можно выбрать
подсчет количества комбинаций
комбинаторное правило умножения - если нужно выбрать k элементов из некоторого множества элементов, и 1-ый элемент можно выбрать 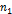 способами, …, k -ый элемент -
способами, …, k -ый элемент - 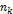 способами, то число всех возможных комбинаций равно
способами, то число всех возможных комбинаций равно  пр: сколько вариантов обеда можно составить, если в столовой есть 2 первых блюда, 4 вторых блюда и 3 напитка?
пр: сколько вариантов обеда можно составить, если в столовой есть 2 первых блюда, 4 вторых блюда и 3 напитка?  факториал
факториал  пр:
пр:  Виды комбинаций:
Виды комбинаций:
| перестановки из n различных элементов | 
|
| пр: сколькими способами можно расставить 5 книг на полке? | |
перестановки с повторениями
если 1-ый элемент повторяется  раз, …, k -ый элемент - раз, …, k -ый элемент -  раз раз
| 
|
| пр: сколькими способами можно расположить в ряд 3 белых и 2 черных шара?
| |
| размещения выбор k элементов из n различных элементов, порядок важен | 
|
| пр: сколькими способами можно выбрать председателя и заместителя из 5 человек?
| |
| размещения с повторениями если элементы могут повторяться | 
|
| пр: сколько трехзначных чисел можно записать с помощью цифр 1, 2, 3, 4, 5?
| |
| сочетания выбор k элементов из n различных элементов, порядок не важен | 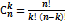
|
пр: сколькими способами можно выбрать 3 дежурных из 5 человек?

| сочетания с повторениями если элементы могут повторяться | 
|
| пр: сколькими способами можно собрать букет из 3 роз, если в магазине есть розы 5-ти цветов?
| |
Бином Ньютона 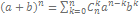
(коэффициенты из треугольника Паскаля)
 отношение числа исходов, благоприятных (подходящих) событию, к общему числу исходов
пр: событию А подходят 2 исхода (выпадет 1 или 2)
отношение числа исходов, благоприятных (подходящих) событию, к общему числу исходов
пр: событию А подходят 2 исхода (выпадет 1 или 2)  вероятность события А
вероятность события А  статистическое определение вероятности (из эксперимента): отношение числа испытаний, в которых произошло событие, к числу всех испытаний
пр: при проверке партии семян выяснилось, что из 1000 посаженных семян взошло 805
статистическое определение вероятности (из эксперимента): отношение числа испытаний, в которых произошло событие, к числу всех испытаний
пр: при проверке партии семян выяснилось, что из 1000 посаженных семян взошло 805
 вероятность того, что семечко из этой партии взойдет:
вероятность того, что семечко из этой партии взойдет:  свойства вероятности:
- достоверное событие:
свойства вероятности:
- достоверное событие:
 (обязательно произойдет)
- невозможное событие:
(обязательно произойдет)
- невозможное событие:
 (обязательно не произойдет)
- противоположное событие:
(обязательно не произойдет)
- противоположное событие:
 - произведение (пересечение) событий:
- произведение (пересечение) событий:
 «произойдет и A, и В»
условная вероятность (наступления события B при условии наступления события A )
«произойдет и A, и В»
условная вероятность (наступления события B при условии наступления события A )
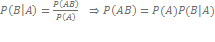 если A и B - независимые события (наступление события A не меняет вероятность наступления события B ), то
если A и B - независимые события (наступление события A не меняет вероятность наступления события B ), то
 - сумма (объединение) событий:
- сумма (объединение) событий:
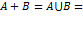 «произойдет или A, или В»
«произойдет или A, или В»
 если A и B - несовместные события (не могут произойти одновременно), то
если A и B - несовместные события (не могут произойти одновременно), то
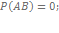
 - разность событий:
- разность событий:
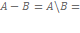 «A произойдет, В не произойдет»
«A произойдет, В не произойдет»
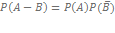

 ( n - показатель, a - подкоренное выражение)
( n - показатель, a - подкоренное выражение)
 при
при 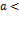 0 определен только для нечетных n
0 определен только для нечетных n

 пр:
пр: 

Последовательности
числовая последовательность - упорядоченный набор чисел (c заданным правилом вычисления каждого следующего числа)
пр: числа Фибоначчи (сумма двух предыдущих)
1, 1, 2, 3, 5, 8, 13, 21…

Арифметическая прогрессия:
 ( d - «разность»)
( d - «разность»)

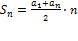
Геометрическая прогрессия:
 ( q - «знаменатель»)
( q - «знаменатель»)
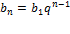

бесконечно убывающая: при 

предел последовательности - число, к которому стремятся члены последовательности
при 



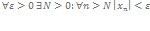
число Эйлера 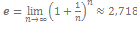
 среднее геометрическое
среднее геометрическое  среднее гармоническое
среднее гармоническое 
Таблица квадратов

|
Таблица степеней
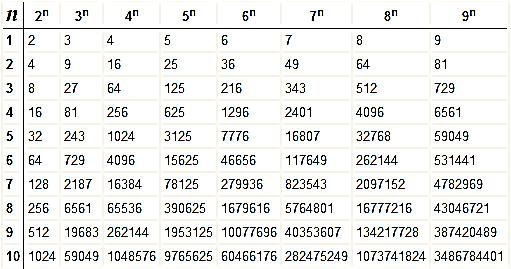
|
Алгебра - 10 класс
Рациональные уравнения
распадающиеся уравнения


Рациональные неравенства
метод интервалов для неравенств вида

 - точки перемены знака
- точки перемены знака
пр: 
«четные» точки:  (т.к. эта скобка входит в выражение в четной степени)
(т.к. эта скобка входит в выражение в четной степени)
«нечетные» точки: 
скобка  входит и в числитель, и в знаменатель – в общем, она входит в выражение в 1ой степени
входит и в числитель, и в знаменатель – в общем, она входит в выражение в 1ой степени
выражение меняет знак только в «нечетных» точках
- отмечаем на оси точки перемены знака
- если неравенство нестрогое, то закрасим точки, которые входят только в числитель (в этих точках выражение равно нулю), а точки из знаменателя оставим незакрашенными (знаменатель не должен быть равен нулю, т.к. в этих точках значение выражения не определено)
- на самом правом промежутке выражение положительно (т.к. все скобки положительны)
- «идем» справа налево через точки перемены знака: в «нечетных» точках знак меняется, в «четных» точках знак остается прежним
пр:

можно условно изобразить дугами промежутки знакопостоянства (в «четных» точках ставим «петлю», чтобы не забыть вставить отдельную точку в ответ)

- записываем ответ в соответствии со знаком исходного неравенства, включая закрашенные точки и исключая незакрашенные
пр: 
если неравенство имеет не совсем подходящий вид, то его нужно преобразовать:
пр: 
разделим нер-во на  (при умножении или делении на отрицательное число знак нер-ва меняется)
(при умножении или делении на отрицательное число знак нер-ва меняется)

«перевернем» скобку (т.е. умножим нер-во на 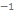 )
)

«вынесем» 5 за скобку

 теперь можно
теперь можно
применить метод интервалов 
Система (уравнений или неравенств)  пересечение решений
пересечение решений
пр: 



Совокупность (уравнений или неравенств)  объединение решений
объединение решений
пр: 



Метод замены неизвестных
пр: 
замена 




пр: 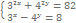 замена
замена 

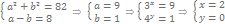
пр:  замена
замена 
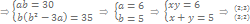
Возвратные (симметричные)
Уравнения n -ой степени

если 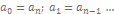 то
то
· если n четно - разделить уравнение на 
и сделать замену переменной 
· если n нечетно – то один из корней равен -1 и при делении  на
на  получится возвратное уравнение четной степени
получится возвратное уравнение четной степени
пр: 
симметричное ур-е нечет. степени  корень -1
корень -1

 выделим полный квадрат
выделим полный квадрат



Ответ: 
Функция  (степенная)
(степенная)


Последнее изменение этой страницы: 2020-02-17; Просмотров: 185; Нарушение авторского права страницы