
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Показательные уравнения и неравенства ⇐ ПредыдущаяСтр 3 из 3
пр: метод приведения к одному основанию: пр: пр: (если основание < 1, при «отбрасывании оснований» знак неравенства меняется) | |||||||||||||
| Функция ( Логарифмические уравнения и неравенства
пр: пр: (если основание < 1, то знак неравенства меняется) метод приведения к одному основанию: пр: пр: ОДЗ: сравнение логарифмов с разными основаниями: пр: | |||||||||||||
Логарифмы
 - «степень, в которую нужно возвести a, чтобы получить b » - «степень, в которую нужно возвести a, чтобы получить b » 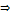
  (основное логарифмическое тождество)
a - «основание логарифма»
b - «выражение под логарифмом»
пр:
(основное логарифмическое тождество)
a - «основание логарифма»
b - «выражение под логарифмом»
пр:  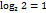 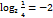  свойства логарифмов:
свойства логарифмов:
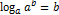




 (переход к другому основанию) (переход к другому основанию)
 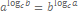 специальные обозначения:
специальные обозначения:
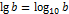 (десятичный логарифм) (десятичный логарифм)
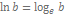 (натуральный логарифм, (натуральный логарифм,  )
пр: )
пр:  ( (  стандартный вид числа) стандартный вид числа)  
| |||||||||||||
|
Тригонометрия | радиан - величина угла, соответствующего дуге окружности, длина которой равна радиусу
(не зависит от окружности)
синус ( sin ),
косинус ( cos ),
тангенс ( tg ),
котангенс ( ctg )
(угла на единичной окружности) - это координаты соответствующего радиус-вектора по осям синусов (x=0), косинусов (y=0), тангенсов (x=1), котангенсов (y=1)


 ( не опред. при
( не опред. при  ) )
 ( не опред. при
( не опред. при 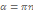 ) )

| ||||||||||||
|
Тригонометрические функции
|
Обратные тригонометрические функции | ||||||||||||
|
Тригонометрические уравнения
или
| ||||||||||||
|
Тригонометрические формулы
| |||||||||||||
Алгебра - 1 1 класс
Равносильность уравнений и неравенств
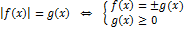


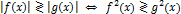 распадающиеся, дробные
распадающиеся, дробные
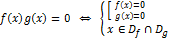


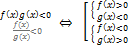 сокращение
сокращение
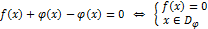

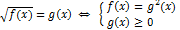
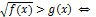

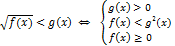 показательные
показательные
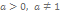

 логарифмические
логарифмические
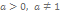

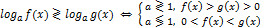 равносильные уравнения/неравенства/системы - имеют одинаковые множества корней
использование формул (свойств корней, логарифмов, тригонометрических функций) может привести к неравносильным преобразованиям
равносильные уравнения/неравенства/системы - имеют одинаковые множества корней
использование формул (свойств корней, логарифмов, тригонометрических функций) может привести к неравносильным преобразованиям
|
Производная | |||||||||||||||||||||||||||||||||||||||||||||||||||
производная (функция): функция, которая в каждой точке равна значению производной от «первообразной» функции в этой точке пр: первообразная производная уравнение касательной к функции
| геометрический смысл: тангенс угла наклона касательной  (угловой коэффициент касательной прямой (угловой коэффициент касательной прямой  )
физический смысл: скорость изменения функции
пр: )
физический смысл: скорость изменения функции
пр: 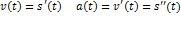 скорость - производная от перемещения по времени, ускорение - производная от скорости по времени
дифференцирование - нахождение производной
правила дифференцирования:
можно пользоваться таблицей производных (см→ )
скорость - производная от перемещения по времени, ускорение - производная от скорости по времени
дифференцирование - нахождение производной
правила дифференцирования:
можно пользоваться таблицей производных (см→ )
пр: Приближенные вычисления
пр: | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интеграл | |||||||||||||||||||||||||||||||||||||||||||||||||||
интегрирование - нахождение функции (первообразной) по ее производной правила интегрирования: можно пользоваться таблицей интегралов (см→ )
пр:
пр:
пр: формула интегрирования по частям:
пр: | определенный интеграл (формула Ньютона-
площадь фигуры между графиками функций: если
физический смысл интеграла: сумма пр: перемещение - интеграл от скорости, работа - интеграл от силы свойства определенного интеграла:
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| таблица производных и интегралов
| предел функции в точке (или на бесконечности) - величина, к которой стремится значение функции, когда аргумент стремится к этой точке (слева и справа)
пр: «замечательные» пределы:
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование графика функции
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
Исследование функции 1) область определения, непрерывность
2) четность/нечетность, периодичность
3) точки пересечения с осями, промежутки знакопостоянства точка пересечения с осью y: точки пересечения с осью x: 4) критические точки, промежутки возрастания/убывания
5) точки перегиба, промежутки выпуклости/вогнутости
6) область значений, ограниченность сверху/снизу, экстремумы
нахождение минимума/максимума функции: сравнить значения функции в критических точках и на границах области определения, в точках разрыва 7) асимптоты (прямые, к которым стремится функция)
8) график (для более точного построения можно найти значения функции в некоторых точках) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2020-02-17; Просмотров: 142; Нарушение авторского права страницы