|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Моделирование геодезической сети.
Моделирование геодезической сети выполняется на карте масштаба 1: 50 000. В заданном районе с требуемой плотностью проектируется сеть триангуляции, и определяются проектные значения координат пунктов. Дирекционные углы и длины сторон вычисляется из решения обратных геодезических задач. Их проектные значения используются в дальнейших вычислениях. Схема сети:
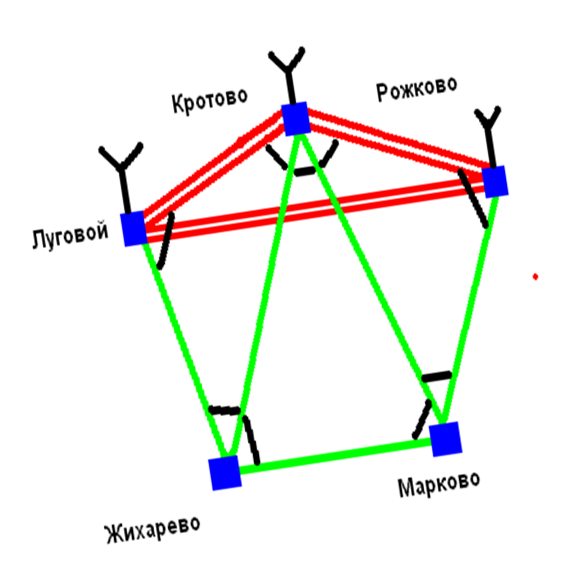
Координаты пунктов данной сети определяются по карте масштаба 1: 50 000. Они имеют следующие значения: Исходные пункты:
Определяемые пункты: х=5 342 374.27м у=6 393 907.75м х=5 342 287.59м у=6 390 919.12м Значения дирекционных углов и длин сторон вычисляются по формулам обратной геодезической задачи: yj-yi
Решение обратных геодезических задач
Составление параметрических уравнений поправок направлений. Параметрические уравнения поправок направлений имеют вид:
где
а и b — коэффициенты параметрических уравнений поправок, вычисляемые по формулам: где
Параметрические уравнения поправок направлений: V15= − δ z1 + a51ξ 5 + b51η 5 +l15 V12= − δ z1 + l12 V23= − δ z2 + l23 V24= − δ z2 + a42ξ 4 + b42η 4+ l24 V25= − δ z2 + a52ξ 5 + b52η 5 + l25 V21= − δ z2 + l21 V34= − δ z3 + a43ξ 4 + b43η 4 + l34 V32= − δ z3 + l32 V43= − δ z4 + a43ξ 4 + b43η 4 + l43 V42= − δ z4 + a42ξ 4 + b42η 4 + l42 V45= − δ z4 + a45ξ 4 + b45η 4 + a54ξ 5 + b54η 5 + l45 V51= − δ z5 + a51ξ 5 + b51η 5 + l51 V52= − δ z5 + a52ξ 5 + b52η 5 + l52 V54= − δ z5 + a54ξ 5 + b54η 5 + a45ξ 4 + b45η 4 + l54 Таблица коэффициентов параметрических уравнений поправок
Составление параметрических уравнений поправок измеренных дирекционных углов. Уравнение поправок дирекционного угла отличается от уравнения поправок направлений тем, что в нем нет поправки в ориентирующий угол. Записывается оно следующим образом:
Параметрические уравнения поправок измеренных дирекционных углов: V15= a51ξ 5 + b51η 5 + l15 V12= l12 V23= l23 V24= a42ξ 4 + b42η 4 + l24 V25= a52ξ 5 + b52η 5 + l25 V21= l21 V34= a43ξ 4 + b43η 4 + l34 V32=l32 V43= a43ξ 4 + b43η 4 + l43 V42= a42ξ 4 + b42η 4 + l42 V45= a45ξ 4 + b45η 4 + a54ξ 5 + b54η 5 + l45 V51= a51ξ 5 + b51η 5 + l51 V52= a52ξ 5 + b52η 5 + l52 V54= a54ξ 5 + b54η 5 + a45ξ 4 + b45η 4 + l54 Таблица коэффициентов параметрических уравнений поправок
Составление параметрических уравнений Поправок измеренных длин сторон. В проектируемой сети могут планироваться измерения отдельных длин сторон. Параметрическое уравнение поправок стороны имеет вид: где с и d — коэффициенты уравнений, вычисляемые по формулам
а l - исключаемая постоянная систематическая ошибка, обусловленная разностью уровней принимаемых сигналов при проведении измерений и определении поправок. Параметрические уравнения поправок измеренных длин сторон: VS51= c15ξ 5 + d15η 5 + l51= cosα 15ξ 5 + sinα 15η 5 + l15 VS52= c25ξ 5 + d25η 5 + l25= cosα 25ξ 5 + sinα 25η 5 + l25 VS42= c24ξ 4 + d24η 4 + l24= cosα 24ξ 4 + sinα 24η 5 + l24 VS43= c34ξ 4 + d34η 4 + l34= cosα 34ξ 4 + sinα 34η 4 + l34 VS35= c35ξ 5 + d35η 5 + l35= cosα 35ξ 5 + sinα 35η 5 + l35 VS45= c45ξ 4 + d45η 4 + c54ξ 5 + d54η 5 + l45= − cosα 45ξ 4 − sinα 45η 4 + cosα 45ξ 5 + sinα 45η 5 + l45 Таблица коэффициентов параметрических уравнений поправок
Установление единицы веса и вычисление исходной весовой матрицы P для уравниваемых величин. Измеряемые углы на пунктах триангуляции представляются рядом равноточных независимых направлений. Поэтому в качестве единицы веса целесообразно взять вес измерения направлений. Тогда корреляционная матрица ошибок направлений, а следовательно, и ее весовая матрица PМ, будут равны единичной матрице Q = PМ = Е. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2020-02-17; Просмотров: 110; Нарушение авторского права страницы
α i, j=arctg xj-xi si, j=√ (xj-xi)2+(yj-yi)2
— поправка в направление; 
— поправка к предварительному значению ориентирующего угла; 
— поправки к предварительным значениям координат определяемых пунктов; 
; 
, 
и 
— модельные значения дирекционных углов и длин сторон проектируемой сети; 
— свободный член уравнения поправок.
, 
