Расчет автоколебательной системы ВДРП и ее динамических характеристик
Расчет автоколебательной системы воздушно-динамического РП проведем по следующему алгоритму:
1. Рассчитаем частоту автоколебаний:
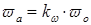 (1.9.1) (1.9.1)
где  = 6÷ 10; = 6÷ 10;
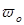 - круговая частота, находится для режима наименьшей точности: - круговая частота, находится для режима наименьшей точности:
 = 70°, Т = +50°, = 70°, Т = +50°, 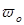 = 2π f = 2π 14, 06 = 88, 3 рад/с. = 2π f = 2π 14, 06 = 88, 3 рад/с.
Примем  = 6, тогда = 6, тогда  = 6ּ 88, 3 = 530 рад/с/ = 6ּ 88, 3 = 530 рад/с/
2. Определим требуемое время эквивалентного запаздывания управляющего электромагнита:
 (1.9.2) (1.9.2)
где φ нел - фазовая характеристика нелинейного элемента,
φ нел = - arcsin λ, λ. = 0, 1 ÷ 0, 15;
φ к  - фазовая характеристика корректирующего фильтра на частоте автоколебаний; - фазовая характеристика корректирующего фильтра на частоте автоколебаний;
 ; ;
φ п  - фазовая характеристика привода на частоте автоколебаний; - фазовая характеристика привода на частоте автоколебаний;
φ к  = arctg = arctg 
Найдем передаточную функцию привода:
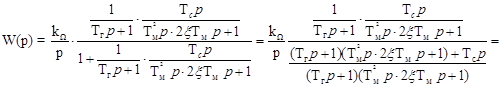

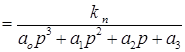 ; ;
 ; ;  ; ;  ; ; 
 ; ;  ; ;  ; ;  ; ;
 ; ;  ; ;
 ; ; 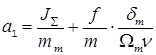 ; ;
 ; ;  ; kn= ; kn=  $ $
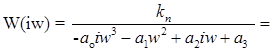
 ; ;  ; ;
Определим фазово-частотную характеристику привода при следующих данных:  кг/см = 3, 3Нּ м; кг/см = 3, 3Нּ м;  кг/см = 0, 72 Нּ м; кг/см = 0, 72 Нּ м;  рад/с; f = 0, 01 кгּ смּ c рад/с; f = 0, 01 кгּ смּ c  Нּ мּ c2; Нּ мּ c2;  = =0, 0436 рад; = =0, 0436 рад; 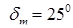 = 0, 44 рад. = 0, 44 рад.
 ; ; 

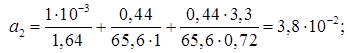
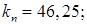   

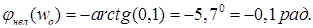
Время эквивалентного запаздывания электромагнита:

без влияния корректирующего фильтра.
3. Рассчитаем амплитуду автоколебаний по зависимости:
 (1.9.3) (1.9.3)
 - амплитудная характеристика привода на частоте автоколебаний. - амплитудная характеристика привода на частоте автоколебаний.
 ; ; 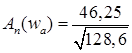 =4, 08 =4, 08
tо- время движения якоря электромагнита от упора до нейтрального положения, tо = 1, 15 мс;
 =0, 21 рад =120 =0, 21 рад =120
4. Определим потребную амплитудную характеристику разомкнутого привода на рабочей частоте из условия обеспечения требуемого фазового сдвига замкнутого рулевого привода.
 , (1.9.4) , (1.9.4)
где 
 - фазовая характеристика электромагнита на рабочей частоте; - фазовая характеристика электромагнита на рабочей частоте;
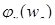 - фазовая характеристика нелинейного элемента - фазовая характеристика нелинейного элемента 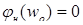 ; ;
 - фазовая характеристика привода на рабочей частоте; - фазовая характеристика привода на рабочей частоте;
 ; ; 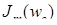 = - 0, 28; = - 0, 28; 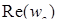 =0, 076; =0, 076;
 -74, 80= 1, 3 рад; -74, 80= 1, 3 рад;  = 88, 3·2, 3·10-3= - 0, 2 рад = - 11, 50 = 88, 3·2, 3·10-3= - 0, 2 рад = - 11, 50
 = -74, 8-11, 5 = -86, 30 = -74, 8-11, 5 = -86, 30
Потребная амплитудная характеристика разомкнутого привода на рабочей частоте будет равна:

5. Определим необходимость установки корректирующего фильтра:
 , (1.9.5) , (1.9.5)
где  ; ;  ; ; 
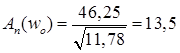 ; ;
 ; ;  =1, 065 =1, 065
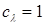 ; ;  . .
Так как ск > 1, то делаем вывод о том, что необходимо ставить корректитрующий фильтр.
7. Ставим корректирующий фильтр вида  , ,
где постоянные времени определим по зависимости:
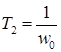 ; ;  ; ;  , ,
тогда  , , 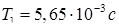 . .
Определим фазовую характеристику фильтра на рабочей частоте:
 ; ;
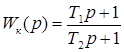 ; ;
 ; ;  ; ; 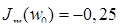 ; ;  ; ;
 . .
Амплитудная характеристика фильтра на рабочей частоте:
 . .
Фазовая характеристика фильтра на частоте автоколебаний:
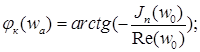   ; ;

Амплитудная характеристика фильтра на частоте автоколебаний:
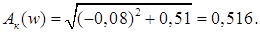
Определим параметр корректирующего фильтра на частоте автоколебаний:
ск 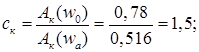
Значит, выбранный параметр подходит для системы.
Определим амплитудно-фазовые характеристики системы с учетом корректирующего фильтра. Расчет произведем по следующим зависимостям:
 ; ;
 ; ;
tg 
 = - 104, 70; = - 104, 70;
 ; ;
tg  = - 0, 354; = - 0, 354;  = - 19, 40. = - 19, 40.
Так как полученный фазовый сдвиг на рабочей частоте удовлетворяет требованиям, то выбранный фильтр подходит для системы.
8. Теперь необходимо рассчитать и построить динамические характеристики привода для различных режимов работы и при различных входных сигналах. Для расчета динамических характеристик воспользуемся программой, предназначенной для расчета амплитудно-фазовых характеристик замкнутой системы. Для каждого режима будем считать динамические характеристики при трех различных входных сигналах: Uвx1 = 0, 088 рад; U вx2 = 0, 314 рад; U вx2 = 0, 44 рад.
1 режим:  ; Т = +50° С; t = 9, 8 с; f = 14, 06 Гц, Ω м = 65, 6 рад/с; ; Т = +50° С; t = 9, 8 с; f = 14, 06 Гц, Ω м = 65, 6 рад/с;
Мm = 3, 3 Н•м; Мн = 0, 72 Н•м; Ризб = 4, 85 атм; w0 = 88, 3 рад/с.
Рассчитаем необходимые данные для ввода:
 
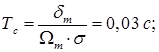  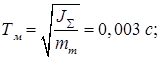
 
Результаты расчета приведены в таблицах 1.9.1-1.9.3.
Таблица 1.9.1
| UBX = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 8
| 1, 7
| 0, 94
| -0, 54
| -10, 9
| | 10
| 1, 8
| 0, 96
| -0, 35
| -13, 5
| | 12
| 1, 88
| 0, 97
| -0, 26
| -16, 2
| | 14, 06
| 1, 95
| 0, 98
| -0, 175
| -17, 7
| | 16
| 2
| 0, 99
| -0, 09
| -21
|
Таблица 1.9.2
| Uвх = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 8
| 1, 7
| 0, 94
| -0, 54
| -9, 5
| | 10
| 1, 8
| 0, 96
| -0, 35
| -11
| | 12
| 1, 88
| 0, 96
| -0.35
| -9, 8
| | 14, 06
| 1, 95
| 0, 99
| -0, 09
| -10
| | 16
| 2
| 1, 01
| 0, 09
| -15
| | Таблица
| 1.9.3
|
|
|
| | Uвх = 0, 44 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 8
| 1, 7
| 0, 98
| -0.175
| -5, 4
| | 10
| 1, 8
| 0, 984
| -0, 14
| -7, 7
| | 12
| 1, 88
| 0, 987
| -0.113
| -11, 1
| | 14, 06
| 1, 95
| 0, 95
| -0, 45
| -13
| | 16
| 2
| 0, 966
| -0, 3
| -9, 4
| | | | | | | | | | |
2 режим:  = 70°; Т = -50° С; t = 0, 6 с; f = 3, 59 Гц, = 70°; Т = -50° С; t = 0, 6 с; f = 3, 59 Гц, 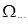 = 65, 631, 5 рад/с; Мт = 0, 82 Н•м; Мн = 0, 324 Н•м; Ризб = 1, 22 атм; w0 = 22, 57 рад/с, Тн = 4, 5-10-3с, = 65, 631, 5 рад/с; Мт = 0, 82 Н•м; Мн = 0, 324 Н•м; Ризб = 1, 22 атм; w0 = 22, 57 рад/с, Тн = 4, 5-10-3с,  = 0, 15, = 0, 15,  = 722, 5. = 722, 5.
Результаты расчета приведены в таблицах 1.9.4-1.9.6.
Таблица 1.9.4
| UBX = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 1, 6
| 1, 0
| 0, 88
| -1, 11
| -3, 5
| | 2.5
| 1, 2
| 0, 9
| -0, 91
| ■ 5, 7
| | 3.59
| 1, 35
| 0, 91
| -0, 82
| -9, 08
| | 4
| 1, 4
| 0, 916
| -0, 76
| -9, 3
| | 6, 33
| 1, 6
| 0, 93
| -0, 63
| -15, 2
|
Таблица 1.9.5
| UBX = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 1, 6
| 1, 0
| 0, 88
| -1, 11
| -3, 2
| | 2, 5
| 1, 2
| 0, 9
| -0, 92
| -5, 3
| | 3, 59
| 1, 35
| 0, 91
| -0, 82
| -7, 3
| | 4
| 1, 4
| 0, 914
| -0, 78
| -7, 6
| | 6, 33
| 1, 6
| 0, 95
| -0, 44
| -9, 3
|
Таблица 1.9.6
| Ubx = 0, 44 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 1.6
| 1, 0
| 0, 9
| -0, 92
| -3, 0
| | 2, 5
| 1, 2
| 0, 93
| -0, 63
| -4, 8
| | 3, 59
| 1, 35
| 0, 95
| -0, 44
| -5, 6
| | 4
| 1, 4
| 0, 97
| -0, 26
| -5, 4
| | 6, 33
| 1, 6
| 1, 016
| -0, 14
| -8, 7
|
3 режим:  = 70°; Т = -50°С; t = 11, 58 с; f = 11, 57 Гц, = 70°; Т = -50°С; t = 11, 58 с; f = 11, 57 Гц,  = 59, 6 рад/с; = 59, 6 рад/с;
Мт = 2, 49 Н•м; Мн = 0, 764 Н•м; Ризб = 3, 699 атм;
w0 = 72, 76 рад/с, 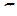 = 0, 307, mт = 1, 74, Тс = 0, 024с, Тг = 0, 0074с, = 0, 307, mт = 1, 74, Тс = 0, 024с, Тг = 0, 0074с,
Тн = 2, 9 -10-3 с,  = 0, 098, kΩ = 1367. = 0, 098, kΩ = 1367.
Результаты расчета приведены в таблицах 1.9.7-1.9.9.
Таблица 1.9.7
| Ubx = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 87
| -1, 2
| -6, 8
| | 6, 33
| 1, 6
| 0, 89
| -1, 01
| -10, 7
| | 10.04
| 1, 8
| 0, 918
| -0, 74
| -16, 5
| | 11, 5
| 1, 85
| 0, 93
| -0, 63
| -19, 0
| | 15, 9
| 2
| 0, 96
| -0, 35
| -20, 8
| | Таблица 1.9.8
|
|
|
|
| | Ubx = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 88
| -1, 11
| -6, 6
| | 6, 33
| 1, 6
| 0, 9
| -0, 91
| -10, 1
| | 10.04
| 1, 8
| 0, 94
| -0, 54
| -12, 4
| | 11, 5
| 1, 85
| 0, 943
| -0, 51
| -13, 3
| | 15, 9
| 2
| 1, 023
| -0, 19
| -18, 7
| | Таблица 1.9.9
|
|
|
|
| | Ubx = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 93
| -0, 63
| -4, 8
| | 6, 33
| 1, 6
| 0, 94
| -0, 53
| -7, 8
| | 10.04
| 1, 8
| 0, 97
| -0, 26
| -11, 3
| | 11, 5
| 1, 85
| 1, 0
| 0
| -15, 2
| | 15, 9
| 2
| 1, 04
| 0, 34
| -7
|
= 70°; Т = -50°С; t = 11, 58 с; f = 11, 57 Гц, = 59, 6 рад/с;
Мт = 2, 49; Мн = 0, 764 Н•м; Ризб = 3, 699 атм;
w0 = 72, 76 рад/с, 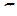 = 0, 307, mт = 1, 74, Тс = 0, 024с, Тг = 0, 0074с, = 0, 307, mт = 1, 74, Тс = 0, 024с, Тг = 0, 0074с,
Тн = 2, 9 -10-3 с,  = 0, 098, = 1367. = 0, 098, = 1367.
4 режим:  = 0°; Т = +50°С; t = 1, 5 с; f = 13, 75Гц, = 0°; Т = +50°С; t = 1, 5 с; f = 13, 75Гц,  = 58, 02 рад/с; = 58, 02 рад/с;
Мт = 30, 05 Н•м; Мн = 4, 8 Н•м; Ризб = 44, 53 атм;
wо = 86, 4 рад/с, 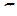 = 0, 16, mm = 10, 9, Тс = 0, 047с, Тг = 0, 0076с, = 0, 16, mm = 10, 9, Тс = 0, 047с, Тг = 0, 0076с,
Тн= 1, 17-10-3с,  = 0, 04, kΩ = 1331. = 0, 04, kΩ = 1331.
Результаты расчета приведены в таблицах 1.9.10-1.9.12.
Таблица 1.9.10
| Ubx = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0.96
| -0, 35
| -3, 6
| | 6, 33
| 1, 6
| 0, 98
| -0, 175
| -5, 05
| | 10.04
| 1, 8
| 1, 01
| 0, 086
| -6, 2
| | 11, 5
| 1, 85
| 1, 05
| 0, 42
| -5, 9
| | 15, 9
| 2
| 1, 063
| 0, 53
| -6, 14
| Таблица 1.9.11
| Ubx = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 98
| -0, 175
| -1, 5
| | 6, 33
| 1, 6
| 0, 99
| -0, 087
| -2, 2
| | 10.04
| 1, 8
| 1, 01
| 0, 086
| -4, 6
| | 11, 5
| 1, 85
| 1, 03
| 0, 26
| -6, 7
| | 15, 9
| 2
| 1, 033
| 0, 28
| -8, 6
|
Таблица 1.9.12
| Ubx = 0, 44 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 98
| -0, 175
| -1, 32
| | 6, 33
| 1, 6
| 1, 0
| 0
| -2, 65
| | 10.04
| 1, 8
| 1, 0
| 0
| -5
| | 11, 5
| 1, 85
| 1, 01
| 0, 086
| -8, 4
| | 15, 9
| 2
| 1, 03
| 0, 256
| -6, 6
|
5 режим:  = 70°; Т = -50°С; t = 5, 8 с; f = 12, 96 Гц, = 70°; Т = -50°С; t = 5, 8 с; f = 12, 96 Гц,  = 55 рад/с; = 55 рад/с;
Mffl = 8, 38 Н•м; Мн = 2, 502 Н • м; Ризб = 12, 41 атм;
w0 = 81, 4 рад/с, σ = 0, 3, mm = 5, 686, Тс = 0, 0267с, Тг = 0, 008с,
Тн = 1, 16 -10'3с, ζ = 0, 054, кΩ = 1261, 5.
Результаты расчета приведены в таблицах 1.9.13-1.9.15.
Таблица 1.9.13
| UBX = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 6, 33
| 1, 6
| 0, 94
| -0, 54
| -7, 8
| | 7, 98
| 1, 7
| 0, 95
| -0, 44
| -10
| | 10, 04
| 1, 8
| 0, 96
| -0, 35
| -13, 2
| | 12, 95
| 1, 9
| 0, 98
| -0, 175
| -18, 2
| | 15, 9
| 2
| 1, 0
| 0
| -21, 8
|
Таблица 1.9.14
| UBX = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 6, 33
| 1, 6
| 0, 94
| -0, 54
| -6, 6
| | 7, 98
| 1, 7
| 0, 96
| -0, 35
| -7, 8
| | 10, 04
| 1, 8
| 1, 0
| 0
| -6, 4
| | 12, 95
| 1, 9
| 1, 0
| 0
| -9, 8
| | 15, 9
| 2
| 1, 01
| 0, 086
| -12, 5
|
Таблица 1.9.15
| UBX = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 6, 33
| 1, 6
| 0, 98
| -0, 175
| -4, 6
| | 7, 98
| 1, 7
| 1, 0
| 0
| -5, 3
| | 10, 04
| 1, 8
| 1, 0
| 0
| -7, 6
| | 12, 95
| 1, 9
| 1, 02
| 0, 172
| -7, 7
| | 15, 9
| 2
| 1, 04
| 0, 34
| -17, 9
|
6 режим:  = 0°; Т = -50°С; t = 10, 1 с; f = 7, 5 Гц, = 0°; Т = -50°С; t = 10, 1 с; f = 7, 5 Гц,  = 58, 055, 92 рад/с; = 58, 055, 92 рад/с;
Mm = 15, 3 Н•м; Мн = 3, 75 Н•м; Ризб= 22, 69 атм;
w0 = 47, 12 рад/с; σ = 0, 245; mm = 8, 52; Тс = 0, 032с;
Тг = 0, 00787с, Тн = 1, 33 •10-3с, ζ = 0, 044, кΩ = 1282.
Результаты расчета приведены в таблицах 1.9.16-1.9.18.
Таблица 1.9.16
| UBX = 0, 088 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 94
| - 0, 54
| - 4, 4
| | 6, 33
| 1, 6
| 0, 95
| - 0, 44
| - 7, 2
| | 7, 5
| 1, 7
| 0, 96
| - 0, 35
| - 8, 7
| | 10, 04
| 1, 8
| 0, 97
| - 0, 26
| - 12, 3
| | 15, 9
| 2
| 1, 005
| 0, 04
| - 21, 5
|
Таблица 1.9.17
| UBX = 0, 314 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 95
| - 0, 44
| - 3, 84
| | 6, 33
| 1, 6
| 0, 98
| - 0, 175
| - 3, 6
| | 7, 5
| 1, 7
| 0, 987
| - 0, 114
| - 3, 16
| | 10, 04
| 1, 8
| 1, 0
| 0
| - 5, 4
| | 15, 9
| 2
| 1, 0
| 0
| - 10, 7
|
Таблица 1.9.18
| UBX = 0, 44 рад
| | f, Гц
| lgw
| Азам
| Lзам, дБ
| φ зам, 0
| | 4
| 1, 4
| 0, 98
| - 0, 175
| - 2, 98
| | 6, 33
| 1, 6
| 0, 99
| - 0, 09
| - 2, 8
| | 7, 5
| 1, 7
| 1, 0
| 0
| - 4, 5
| | 10, 04
| 1, 8
| 1, 0
| 0
| - 6, 7
| | 15, 9
| 2
| 1, 06
| 0, 5
| - 12, 8
|
По результатам расчета построим динамические характеристики привода на различных режимах.

Рис 1.9.1 Динамические характеристики привода.
|

