СИНХРОННЫЙ ПРИЁМ СИМВОЛОВ ДВОИЧНОГО ЦИФРОВОГО КОДА ПРИ ДЕЙСТВИИ БЕЛОГО ШУМА. КРИТЕРИЙ ИДЕАЛЬНОГО НАБЛЮДАТЕЛЯ.

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒

Пусть двоичный цифровой код используется для передачи значения некоторой случайной величины. Тогда ошибочные решения при приёме символа k-го разряда кода могут заключаться либо при приёме 1, когда был передан 0, либо в приёме 0, когда была передана 1. Абсолютное значение вызываемой этим ошибки в передаваемой величине в обоих случаях равно 2^k^-1, различие состоит лишь в знаке этой ошибки. Поэтому стоимость потерь при приёме символа k-го разряда в обоих случаях может быть принята одинаковой . Правильному приёму символа можно приписать нулевые потери . Тогда минимизация среднего риска R сведётся к минимизации среднего числа ошибок в приёме символов каждого разряда независимо от характера этих ошибок. Критерий минимума среднего числа ошибок был назван В.А. Котельниковым критерием “идеального наблюдателя” (т.е. наблюдателя, беспристрастно фиксирующего все ошибки).

Допустим, что передаваемая цифровым кодом случайная величина с равной вероятностью может принимать любое значение от 0 до . В этом случае вероятность передачи в каждом из разрядов символов 0 и 1 одинаковые: . При указанных условиях по формуле (4.15) получим , а 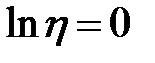и критерий оптимального обнаружения символа любого разряда на фоне белого шума согласно (5.5) примет вид:

(5.6)

Найдём теперь вероятность ошибочного приёма символов двоичного кода (приём 1 вместо 0) и (приём 0 вместо 1).

Рассмотрим два случая передачи символов:

а) двоичный код с “пассивным нулём”: символ 1 передаётся сигналом , имеющим длительность Т и энергию Е, а символ 0 соответствует отсутствию этого сигнала на интервале длительности Т ;

б) двоичный код с “активным нулём”: символы 1 и 0 передаются различными сигналами 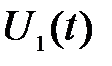и , имеющими одинаковые длительность и энергию.

В первом случае критерий (5.6) принимает вид:

или

(5.7)

В (5.7) для обозначения гипотез вместо и используются принимаемые оценки 1 и 0.

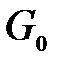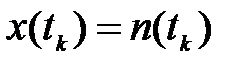Вероятность трансформации нуля в единицу есть вероятность того, что случайная величина , соответствующая левой части (5.7) при отсутствии сигнала в принятой реализации , т.е. при , будет больше . Найдём закон распределения случайной величины:

(5.8)

Так как (5.8) представляет линейное преобразование белого шума, то 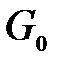является центрированной случайной величиной с нормальным законом распределения:

где - дисперсия случайной величины .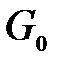

(5.9)

В силу некоррелированности , представляющей дискретную выборку реализации белого шума с интервалами между отсчётами :

Учитывая, что , получаем:

(5.10)

Вероятность того, что случайная величина 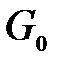с нормальным законом распределения и дисперсией (5.10) будет больше Е/2:

(5.11)

где - интеграл вероятности.

Вероятность 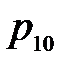трансформации единицы в нуль представляет вероятность того, что случайная величина , соответствующая левой части (5.7) при передаче сигнала , т.е. при будет меньше Е/2.

Случайная величина может быть представлена в виде:

(5.12)

где 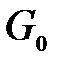определяется из (5.8).

Поэтому условие эквивалентно условию , т.е.:

Таким образом, вероятности трансформации символов и одинаковы и определяются формулой (5.11).

Равенство и - прямое следствие применения критерия идеального наблюдателя, исходящего из равнозначности обеих ошибок.

При достаточно широкой полосе (малом ) сумму левой части (5.7) можно заменить интегралом

(5.13)

по форме записи совпадающим с взаимной корреляционной функцией и имеющим название корреляционного интеграла.

Распознавание символов двоичного кода с “пассивным нулём” сводится, таким образом, к сравнению корреляционного интеграла с пороговым значением, равным половине энергии сигнала .

В случае передачи обоих символов сигналами и с одинаковой энергией Е (двоичный код с “активным нулём”) критерий (5.6) при принимает вид:

(5.14)

Или

(5.15)

То есть, решение принимается в пользу того символа, для которого корреляционный интеграл принимает большее значение. В этом случае есть вероятность того, что при передаче сигнала левая часть (5.14) превысит нуль, а - вероятность того, что при передаче сигнала левая часть (5.14) будет меньше нуля.

При передаче сигнала левая часть (5.14) будет представлять некоторую случайную величину , равную:

(5.16)

где:

(5.17) (5.18)

Величину назовём коэффициентом различимости символов. Если и тождественны (символы неразличимы), то =0. При передаче сигнала левая часть (5.14) будет представлять случайную величину , равную:

(5.19)

Из (5.16) и (5.19) следует, что условие > 0 и < 0, представляющие условие трансформации символов, эквивалентны условию при трансформации 0 в 1 и при трансформации 1 в 0.

Из сравнения (5.8) и (5.18) следует, что случайная величина 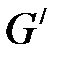получается из 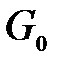заменой на .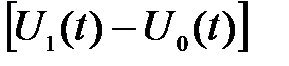

Поэтому дисперсия нормальной случайной величины 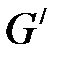на основании (5.9) при переходе от суммы к интегралу равна:

(5.20)

Вероятности трансформации символов по аналогии (5.11) равны:

(5.21)

Рассмотрим геометрический смысл коэффициента различимости символов. Расстояние между сигналами и при совмещении интервалов их существования Т:

(5.22)

Из (5.22) следует, что является мерой расстояния между сигналами. При правая часть (5.12) равна нулю, что соответствует совпадению сигналов (они неразличимы). Максимальное значение получается при строго противофазных сигналов и , и соответствует максимальному расстоянию между ними.

Из формулы (5.21) видно, что чем больше , тем при том же отношении сигнал-шум меньше вероятность трансформации двоичных сигналов. При :

(5.23)

, а при :

, что соответствует “гаданию вслепую”.

При различении символов с использовании фазовой манипуляции несущей на сигналы и противофазны и . Вероятность трансформации символов при этом максимальна (5.23). При частотной манипуляции, когда разность частот много больше величины и сигналы на интервале Т ортогональны, коэффициент различимости . При этом вероятность трансформации символов больше, чем при фазовой манипуляции, но меньше, чем для двоичного кода с “пассивным нулём” (5.11). При АМ - вероятность трансформации символов при этом ещё больше. Только в частном случае импульсной АМ при условии, что импульсы и не перекрываются, т.е. при ортогональности этих сигналов, АМ и ЧМ при равных энергиях сигналов эквивалентны. Критерий (5.6) означает, что выбирается тот из вариантов обнаруживаемых сигналов, которому соответствует меньшее расстояние до данной реализации сигнала . Этот критерий естественен в условиях, когда оба варианта ошибочных решений одинаково опасны, а сами обнаруживаемые сигналы равновероятны.

Формула (5.12) для вероятностей трансформации символов двоичного цифрового кода с “активным нулём” с учётом (5.22) может быть записана:

(5.24)

Таким образом, при обнаружении бинарных сигналов с использованием критерия идеального наблюдателя мерой помехоустойчивости символов служит половина расстояния между обнаруживаемыми сигналами.

Это отражает факт, что трансформация символов наступает тогда, когда реализация из-за действия помехи отличается от передаваемого сигнала более, чем на , и ближайшем к принятой реализации окажется не переданной, а другой сигнал. Критерий принятия решений получен в предположении, что сигналы и совмещены в пространстве сигнала с полезной составляющей , при этом . В задачах приёма символов двоичного кода выполнение этого условия обеспечивается синхронизацией, задающей начало приёма очередного символа.

Решающая схема может быть реализована с использованием коррелятора, вычисляющего корреляционные интегралы, входящие в критерий принятия решения (5.13) и (5.15) и порогового устройства. На рис. 5.1а приведена структура решающего устройства для обнаружения сигналов двоичного кода с “пассивным нулём”, а на рис. 5.1б – двоичного кода с “активным нулём”.

===

В задачах различения наиболее обоснованным является выбор критерия идеального наблюдателя, на основании которого считается верной гипотеза Н₁, если

, (7.3)

откуда следует с учётом (7.1) и (7.2), что гипотеза Н₁ верна, если

(7.4)

Для симметричной системы передачи двоичных сигналов выполняются равенства:

(7.5)

где р(S₁/S₂) - условная вероятность.

⇐ Предыдущая 123 4 5 6 Следующая ⇒