для различных видов правых частей
Таблица 3.1
| №
| Правая часть
диф. уравнения
| Корни характеристического уравнения
| Виды частного решения
|
|
| 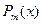
| 1. Число 0 не является корнем характеристического уравнения
| 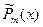
|
2. Число 0 является корнем характеристического уравнения кратности 
| 
|
|
| 
| 1. Число  не является корнем характеристического уравнения не является корнем характеристического уравнения
| 
|
2. Число  является корнем характеристического уравнения кратности является корнем характеристического уравнения кратности 
| 
|
|
| 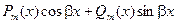
| 1. Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 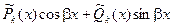

|
2. Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 
| 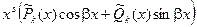

|
|
| 
| 1. Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
|  
|
2. Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 
|  
|
Здесь  - многочлены от
- многочлены от 
 -й степени общего вида с неопределенными коэффициентами.
-й степени общего вида с неопределенными коэффициентами.
Пример 3.15.Найти общее решение уравнение 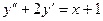 .
.
Решение.Общее решение неоднородного линейного уравнения:  . Соответствующее однородное уравнение имеет вид:
. Соответствующее однородное уравнение имеет вид: 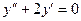 . Составим характеристическое уравнение
. Составим характеристическое уравнение  . Его корни
. Его корни  ,
, 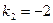 . В силу формулы (3.16)
. В силу формулы (3.16) 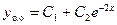 . Частное решение неоднородного уравнения будем искать в виде
. Частное решение неоднородного уравнения будем искать в виде  (см. таблицу 3.1). Находим производные и подставляем в заданное уравнение:
(см. таблицу 3.1). Находим производные и подставляем в заданное уравнение:
 ,
, 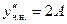 ,
,
 ,
, 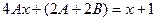 .
.
Приравниваем коэффициенты при одинаковых степенях  в левой и правой части:
в левой и правой части:
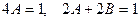 ,
,
откуда  ,
,  ,
,  .
.
Общее решение исходного уравнения будет 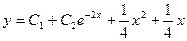 .
.
Пример 3.15.Найти общее решение системы дифференциальных уравнений
 .
.
Решение.Дифференцируя одно из уравнений системы по 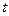 (например, первое уравнение) и исключая функцию
(например, первое уравнение) и исключая функцию  , сведем уравнение системы к решению уравнения второго порядка с постоянными коэффициентами. Решая это уравнение, найдем функцию
, сведем уравнение системы к решению уравнения второго порядка с постоянными коэффициентами. Решая это уравнение, найдем функцию 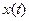 , а затем из первого уравнения найдем и функцию
, а затем из первого уравнения найдем и функцию 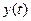 .
.
Итак,
 . .
| (3.19)
|
Из второго уравнения находим  и подставим в уравнение (3.19):
и подставим в уравнение (3.19):
 ;
;  .
.
Наконец, найдем  из первого уравнения систем:
из первого уравнения систем:
 , ,
| (3.20)
|
 .
.
После преобразования получаем однородное уравнение второго порядка с постоянными коэффициентами:
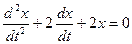 .
.
Решая характеристическое уравнение  , получим
, получим  , откуда
, откуда
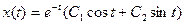 .
.
Функцию 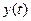 находим, подставляя
находим, подставляя 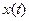 и
и 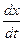 в формулу (3.20), после преобразований получим
в формулу (3.20), после преобразований получим
 .
.
Контрольная работа №4.
«Интегральное исчисление функции одной независимой переменной»
Задача 1. Вычислить неопределенные интегралы
| 1.1
| 1. 
| 2. 
| 3. 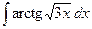
| 4. 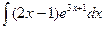
|
| 1.2
| 1. 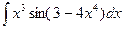
| 2. 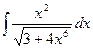
| 3. 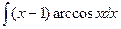
| 4. 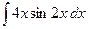
|
| 1.3
| 1. 
| 2. 
| 3. 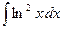
| 4. 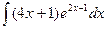
|
| 1.4
| 1. 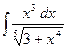
| 2. 
| 3. 
| 4. 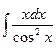
|
| 1.5
| 1. 
| 2. 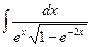
| 3. 
| 4. 
|
| 1.6
| 1. 
| 2. 
| 3. 
| 4. 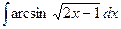
|
| 1.7
| 1. 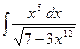
| 2. 
| 3. 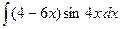
| 4. 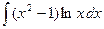
|
| 1.8
| 1. 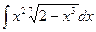
| 2. 
| 3. 
| 4. 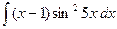
|
| 1.9
| 1. 
| 2. 
| 3. 
| 4. 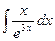
|
| 1.10.
| 1. 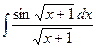
| 2. 
| 3. 
| 4. 
|
| 1.11.
| 1. 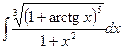
| 2. 
| 3. 
| 4. 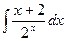
|
| 1.12.
| 1. 
| 2. 
| 3. 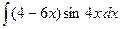
| 4. 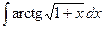
|
| 1.13.
| 1. 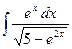
| 2. 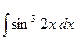
| 3. 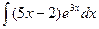
| 4. 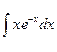
|
| 1.14.
| 1. 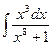
| 2. 
| 3. 
| 4. 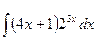
|
| 1.15.
| 1. 
| 2. 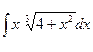
| 3. 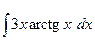
| 4. 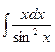
|
| 1.16.
| 1. 
| 2. 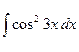
| 3. 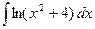
| 4. 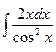
|
| 1.17.
| 1. 
| 2. 
| 3. 
| 4. 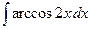
|
| 1.18.
| 1. 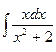
| 2. 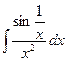
| 3. 
| 4. 
|
| 1.19.
| 1.  
| 2. 
| 3. 
| 4. 
|
| 1.20.
| 1. 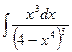
| 2. 
| 3. 
| 4. 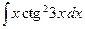
|
| 1.21.
| 1. 
| 2. 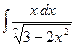
| 3. 
| 4. 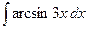
|
| 1.22.
| 1. 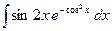
| 2. 
| 3. 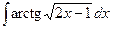
| 4. 
|
| 1.23.
| 1. 
| 2. 
| 3. 
| 4. 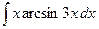
|
| 1.24.
| 1. 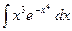
| 2. 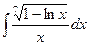
| 3. 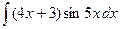
| 4. 
|
| 1.25.
| 1. 
| 2. 
| 3. 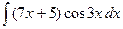
| 4. 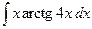
|
| 1.26.
| 1. 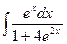
| 2. 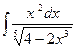
| 3. 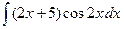
| 4. 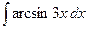
|
| 1.27.
| 1. 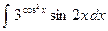
| 2. 
| 3. 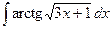
| 4. 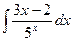
|
| 1.28.
| 1. 
| 2. 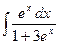
| 3. 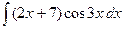
| 4. 
|
| 1.29.
| 1. 
| 2. 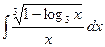
| 3. 
| 4. 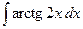
|
| 1.30.
| 1. 
| 2. 
| 3. 
| 4. 
|
Задача 2. Вычислить неопределенные интегралы
| 2.1.
| 1.
| 2.
|
| 2.2.
| 1.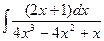
| 2.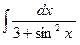
|
| 2.3.
| 1.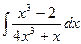
| 2.
|
| 2.4.
| 1.
| 2.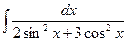
|
| 2.5.
| 1.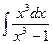
| 2.
|
| 2.6.
| 1.
| 2.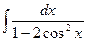
|
| 2.7.
| 1.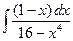
| 2.
|
| 2.8.
| 1.
| 2.
|
| 2.9.
| 1.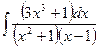
| 2.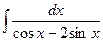
|
| 2.10.
| 1.
| 2.
|
| 2.11.
| 1.
| 2.
|
| 2.12.
| 1.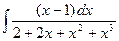
| 2.
|
| 2.13.
| 1.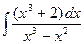
| 2.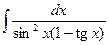
|
| 2.14.
| 1.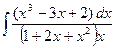
| 2.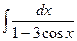
|
| 2.15.
| 1.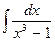
| 2.
|
| 2.16.
| 1.
| 2.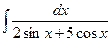
|
| 2.17.
| 1.
| 2.
|
| 2.18.
| 1.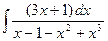
| 2.
|
| 2.19.
| 1.
| 2.
|
| 2.20.
| 1.
| 2.
|
| 2.21.
| 1.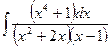
| 2.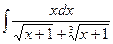
|
| 2.22.
| 1.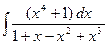
| 2.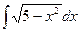
|
| 2.23.
| 1.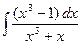
| 2.
|
| 2.24.
| 1.
| 2.
|
| 2.25.
| 1.
| 2.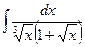
|
| 2.26.
| 1.
| 2.
|
| 2.27.
| 1.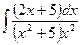
| 2.
|
| 2.28.
| 1.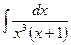
| 2.
|
| 2.29.
| 1.
| 2.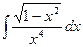
|
| 2.30.
| 1.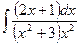
| 2.
|
Задача 3. Вычислить площадь фигур, ограниченных графиками функций
3.1.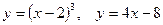
| 3.2.
|
3.3.
| 3.4.
|
3.5.
| 3.6.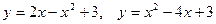
|
3.7.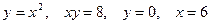
| 3.8.
|
3.9.
| 3.10.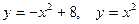
|
3.11.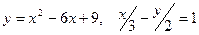
| 3.12.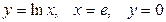
|
3.13. 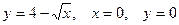
| 3.14.
|
3.15.
| 3.16.
|
3.17.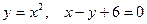
| 3.18.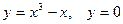
|
3.19. 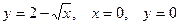
| 3.20.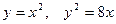
|
3.21.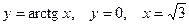
| 3.22.
|
3.23.
| 3.24.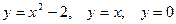
|
3.25.
| 3.26.
|
3.27.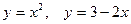
| 3.28.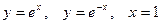
|
3.29.
| 3.30.
|
Задача 4. Вычислить длину дуги кривой, заданной параметрическими уравнениями (для 1-14 вариантов)
4.1. 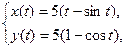 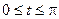 . .
| 4.2.  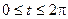 . .
|
4.3.  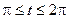 . .
| 4.4. 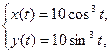  . .
|
4.5.  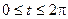 . .
| 4.6.  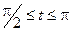 . .
|
4.7.  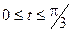 . .
| 4.8. 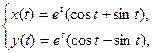 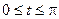 . .
|
4.9.  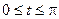 . .
| 3.10.  , ,  . .
|
4.11.  , , 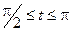 . .
| 4.12.  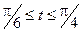 . .
|
4.13.  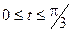 . .
| 4.14. 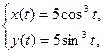  . .
|
Вычислить длину дуги кривой, заданной уравнением в полярных координатах (для 15-30 вариантов)
4.15.  , , 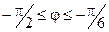 . .
| 4.16. 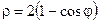 , ,  . .
|
4.17.  , ,  . .
| 4.18. 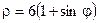 , , 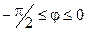 . .
|
4.19. 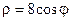 , ,  . .
| 4.20. 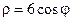 , ,  . .
|
4.21.  , , 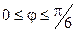 . .
| 4.22. 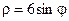 , ,  . .
|
4.23. 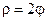 , , 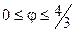 . .
| 4.24.  , , 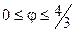 . .
|
4.25.  , ,  . .
| 4.26.  , , 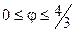 . .
|
4.27.  , ,  . .
| 4.28.  , ,  . .
|
4.29.  , ,  . .
| 4.30.  , ,  . .
|
Контрольная работа №5.
«Дифференциальное исчисление функций многих переменных»
Задача 1. Найти область определения указанных функций.
1.1.
| 1.2.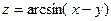
|
1.3.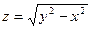
| 1.4.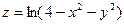
|
1.5.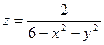
| 1.6.
|
1.7.
| 1.8. 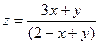
|
1.9.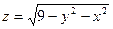
| 1.10.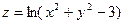
|
1.11.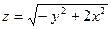
| 1.12.
|
1.13.
| 1.14.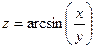
|
1.15.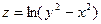
| 1.16.
|
1.17.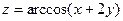
| 1.18.
|
1.19.
| 1.20.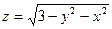
|
1.21.
| 1.22.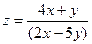
|
1.23.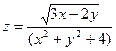
| 1.24.
|
1.25.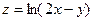
| 1.26.
|
1.27.
| 1.28.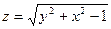
|
1.29.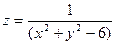
| 1.30.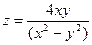
|
Задача 2. Найти частные производные первого порядка функции 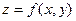 .
.
2.1.
| 2.2.
|
2.3.
| 2.4.
|
2.5.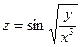
| 2.6.
|
2.7.
| 2.8. 
|
2.9.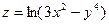
| 2.10.
|
2.11.
| 2.12.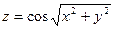
|
2.13.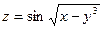
| 2.14.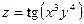
|
2.15.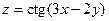
| 2.16.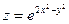
|
2.17.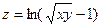
| 2.18.
|
2.19.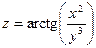
| 2.20.
|
2.21.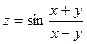
| 2.22.
|
2.23.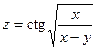
| 2.24.
|
2.25.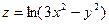
| 2.26.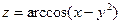
|
2.27.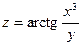
| 2.28.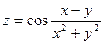
|
2.29.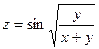
| 2.30.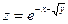
|
Задача 3. Найти градиент функции 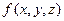 в точке
в точке  . Вычислить производную по направлению вектора
. Вычислить производную по направлению вектора 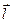 от функции
от функции 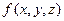 в точке
в точке  .
.
| 3.1.
|  . .
|
| 3.2.
|  . .
|
| 3.3.
| 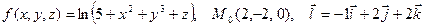 . .
|
| 3.4.
| 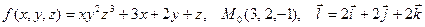 . .
|
| 3.5.
| 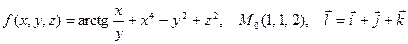 . .
|
| 3.6.
| 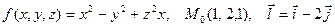 . .
|
| 3.7.
|  . .
|
| 3.8.
| 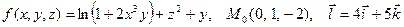 . .
|
| 3.9.
|  . .
|
| 3.10.
| 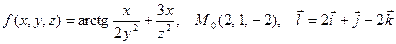 . .
|
| 3.11.
| 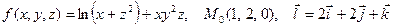 . .
|
| 3.12.
| 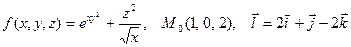 . .
|
| 3.13.
| 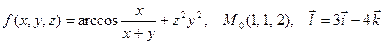 . .
|
| 3.14.
|  . .
|
| 3.15.
|  . .
|
| 3.16.
| 
|
| 3.17.
| 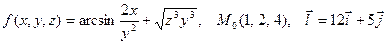 . .
|
| 3.18.
| 
|
| 3.19.
|  . .
|
| 3.20.
|  . .
|
| 3.21.
| 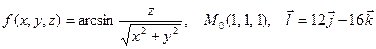 . .
|
| 3.22.
| 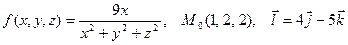 . .
|
| 3.23.
|  . .
|
| 3.24.
|  . .
|
| 3.25.
|  . .
|
| 3.26.
| 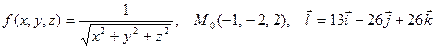 . .
|
| Ё3.27.
|  . .
|
| 3.28.
|  . .
|
| 3.29.
| 
|
| 3.30.
| 
|
Задача 4. Найти частные производные второго порядка функции 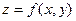 . Убедиться, что
. Убедиться, что 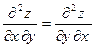 .
.
4.1.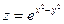
| 4.2.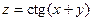
|
4.3.
| 4.4.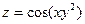
|
4.5.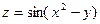
| 4.6.
|
4.7.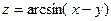
| 4.8. 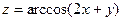
|
4.9.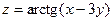
| 4.10.
|
4.11.
| 4.12.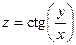
|
4.13.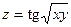
| 4.14.
|
4.15.
| 4.16.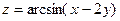
|
4.17.
| 4.18.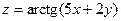
|
4.19.
| 4.20.
|
4.21.
| 4.22.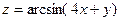
|
4.23.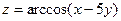
| 4.24.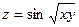
|
4.25.
| 4.26.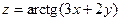
|
4.27.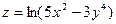
| 4.28.
|
4.29.
| 4.30.
|
Задача 5. Проверить, удовлетворяет ли указанному уравнению данная функция  .
.
| 5.1.
|  . .
|
| 5.2.
| 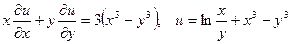 . .
|
| 5.3.
|  . .
|
| 5.4.
|  . .
|
| 5.5.
|  . .
|
| 5.6.
| 
|
| 5.7.
| 
|
| 5.8.
|  . .
|
| 5.9.
| 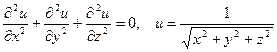
|
| 5.10.
| 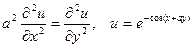 . .
|
| 5.11.
|  . .
|
| 5.12.
| 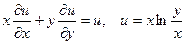 . .
|
| 5.13.
| 
|
| 5.14.
| 
|
| 5.15.
|  . .
|
| 5.16.
| 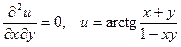 . .
|
| 5.17.
| 
|
| 5.18.
| 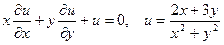 . .
|
| 5.19.
|  . .
|
| 5.20.
| 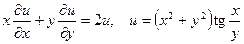 . .
|
| 5.21.
|  . .
|
| 5.22.
|  . .
|
| 5.23.
| 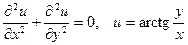 . .
|
| 5.24.
| 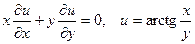 . .
|
| 5.25.
| 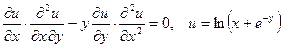 . .
|
| 5.26.
|  . .
|
| 5.27.
|  . .
|
| 5.28.
| 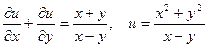 . .
|
| 5.29.
| 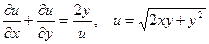 . .
|
| 5.30.
|  . .
|
Задача 6. Найти экстремум функции  .
.
Популярное:

