Дисперсия и поляризация света

⇐ ПредыдущаяСтр 3 из 3

Теоретические вопросы. Дисперсия света; нормальная и аномальная дисперсия; поглощение света; рассеяние света; излучение ускоренно движущегося заряда; диаграмма направленности излучения электрического диполя (линейного осциллятора); линейная поляризация; плоскость поляризации; излучение циркулирующего заряда; круговая поляризация; базисные состояния поляризации; эллиптическая поляризация; естественное или неполяризованное излучение; идеальный поляризатор; закон Малюса; поляризация при отражении; угол Брюстера; степень поляризации; двойное лучепреломление; поляроиды; вращение плоскости поляризации.

Особое внимание следует обратить на следующее. Если заряд движется с ускорением a вдоль оси z, то в его электрическом поле, кроме кулоновской составляющей,

, (2.1)

имеется волновая составляющая

, (2.2)

направленная перпендикулярно радиус-вектору , проведенному от заряда в точку наблюдения P (рис. 2.1).

При r → ∞ становится пренебрежимо малой по сравнению с . Величина представляет собой проекцию вектора ускорения заряда на направление, перпендикулярное направлению распространения волны. Вдоль оси z . Это означает, что заряд не излучает электромагнитные волны в направлении своего ускорения.

Учитывая, что электромагнитной волне требуется время Δ t = r/c (c – скорость света), чтобы дойти до точки наблюдения, для напряженности электрического поля в электромагнитной волне получаем выражение

. (2.3)

Если заряд колеблется гармонически вдоль оси z: z = Acosω t (такой заряд называется линейным осциллятором), его ускорение тоже будет меняться по гармоническому закону:

a = –Aω ²cosω t. (2.4)

Значит, напряженность электрического поля в электромагнитной волне этого заряда будет совершать гармонические колебания, причем колебания вектора будут происходить в фиксированной плоскости, проходящей через ось z и радиус-вектор . При больших r зависимостью амплитуды волны E₀ от r можно пренебречь и волну считать плоской. Фрагмент такой волны в фиксированный момент времени изображен на рис. 2.2. Плоскость, в которой происходят колебания вектора , называется плоскостью поляризации, а волна, испускаемая линейным осциллятором, называется линейно поляризованной.

Пусть теперь заряд движется равномерно по окружности, плоскость которой лежит в плоскости xy (рис. 2.3). При этом заряд обладает центростремительным ускорением, постоянным по величине, но меняющим свое направление. Для направления, лежащего в плоскости вращения заряда, например, вдоль оси y, будет изменяться по гармоническому закону: = acosω t, причем плоскость колебаний проекции будет фиксированной. Таким образом, вдоль оси y будет распространяться линейно поляризованная волна.

Для направления вдоль оси z будет вращаться по окружности, сохраняя свою величину неизменной. Значит, вектор в электромагнитной волне также будет вращаться по окружности, сохраняя свою величину. Так будет происходить в любой точке на оси z. Но, с учетом времени запаздывания, точки, расположенные правее, соответствуют более ранним моментам времени движения заряда. Если соединить концы векторов вдоль оси z, то получится спираль, изображенная на рис. 2.3.

Если смотреть против направления распространения электромагнитной волны, и вектор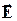

вращается по часовой стрелке, волна называется правополяризованной, а если против часовой стрелки – левополяризованной. На рис. 2.3 в направлении +z распространяется левополяризованная волна, а в направлении –z – правополяризованная.

Если в одном направлении распространяются правополяризованная и левополяризованная волны одинаковой амплитуды и частоты, то суммарная волна будет линейно поляризованной. Это проиллюстрировано на рис. 2.4, где по принципу суперпозиции найден суммарный вектор напряженности электрического поля. Видно, что колебания этого вектора происходят вдоль одного фиксированного направления. Таким образом, при сложении двух волн, поляризованных по кругу, можно получить линейно поляризованную волну.

Наоборот, можно получить волну круговой поляризации при сложении двух линейно поляризованных волн, плоскости поляризации которых взаимно перпендикулярны. Это проиллюстрировано на рис. 2.5, где суммарный вектор в волне круговой поляризации спроецирован на оси x и y. Проекции зависят от времени по закону

E_x = E₀cosω t; (2.5)

E_y = E₀sinω t = E₀cos(ω t – π /2). (2.6)

Следовательно, если вдоль оси +z распространяются две волны одинаковой амплитуды и частоты, поляризованные во взаимно перпендикулярных плоскостях, то в результате получится волна круговой поляризации, если колебания в исходных волнах происходят со сдвигом по фазе π /2. Причем, если колебания в волне, поляризованной вдоль оси x, отстают по фазе на π /2 от колебаний в волне, поляризованной вдоль оси y, то результирующая волна получится левополяризованной, в противном случае волна получится правополяризованной.

Таким образом, волны левой и правой круговой поляризации можно принять за базисные состояния поляризации, поскольку из них можно получить волну любой поляризации, в частности, линейно поляризованную волну. Для этого нужно складывать волны круговой поляризации с соответствующими амплитудами и сдвигами фаз относительно друг друга.

Волны линейной поляризации, поляризованные во взаимно перпендикулярных плоскостях, также можно выбрать в качестве базисных состояний поляризации, поскольку из них тоже можно получить волну любой поляризации, в частности, волну, поляризованную по кругу. В общем случае имеет место эллиптическая поляризация, когда конец вектора в электромагнитной волне при своем вращении описывает эллипс.

Поляризация света может наблюдаться также при его рассеянии. Например, электроны молекул воздуха под действием электрического поля падающего солнечного излучения начинают колебаться и излучать электромагнитные волны. Это излучение называется рассеянным. Оказывается, рассеянное солнечное излучение является частично поляризованным, а для некоторых направлений степень поляризации достигает 100 %.

Чтобы понять причину поляризации рассеянного излучения, необходимо вспомнить, что электромагнитные волны являются поперечными, и что ускоренно движущийся заряд не излучает электромагнитные волны в направлении своего ускорения.

Рассмотрим молекулу воздуха, находящуюся в начале координат (рис. 2.6). Пусть солнечное излучение падает на молекулу вдоль оси z. В солнечном излучении присутствуют волны всевозможной поляризации, и электроны молекулы начнут совершать колебания вдоль этих направлений, т.е. вдоль направлений, расположенных в плоскости xy. Электроны, колеблющиеся вдоль оси y, не будут излучать волны вдоль этой оси. Таким образом, свет, рассеянный молекулой вдоль оси y, будет линейно поляризован вдоль оси x. Для других направлений при J ¹ 90° будет иметь место частичная поляризация.

Таблица 2

Вопросы для самоконтроля	Справочный материал
1 Что такое дисперсия света?	§142 [2]
2 Что такое нормальная и аномальная дисперсия?	§§142, 144 [2]
3 По какому закону происходит поглощение света?	§145 [2]
4 Как происходит рассеяние света?	§146 [2] и данное пособие
5 Сформулируйте закон Релея.	§146 [2]
6 Как происходит излучение ускоренно движущего заряда?	Данное пособие

Окончание табл. 2

7 Как зависит интенсивность излучения линейного осциллятора (электрического диполя) от направления излучения?	§110 [2] и данное пособие
8 Что такое линейно поляризованная волна?	§§105, 134 [2] и данное пособие
9 Что такое плоскость поляризации?	Данное пособие
10 Как получается и что собой представляет волна круговой поляризации?	§134 [2] и данное пособие
11 Что такое базисные состояния поляризации?	Данное пособие
12 Что такое эллиптическая поляризация?	§134 [2] и данное пособие
13 Почему естественный свет является неполяризованным?	§110 [2]
14 Что такое идеальный поляризатор?	§134 [2]
15 Сформулируйте закон Малюса.	§134 [2]
16 Какая доля интенсивности естественного света пройдет через идеальный поляризатор?	§134 [2]
17 Что такое степень поляризации?	§134 [2]
18 Почему при рассеянии получается поляризованный свет?	Данное пособие
19 Сформулируйте закон Брюстера.	§135 [2]
20 Что такое двойное лучепреломление?	§136 [2]
21 Чем объясняется двойное лучепреломление?	§136 [2]
22 Что такое поляроид?	§136 [2]
23 Что такое оптически активные вещества?	§141 [2]
24 От чего зависит угол поворота плоскости поляризации в оптически активных веществах?	§141 [2]

Задачи

2.1 Во сколько раз изменится интенсивность линейно поляризованного света, прошедшего через идеальный поляризатор, ось свободного пропускания которого составляет угол 60° с плоскостью поляризации падающей световой волны?

2.2 Солнечный свет, пройдя через 2 поляризатора, ослаб в 4 раза. Чему равен угол между осями пропускания первого и второго поляризаторов?

2.3 Солнечный свет проходит через два поляризатора, угол между осями пропускания которых равен 60°. Во сколько раз уменьшится интенсивность света?

2.4 Свет падает на поверхность стекла под углом 60°. Чему равен показатель преломления стекла, если отраженный свет максимально поляризован?

Интерференция и дифракция

Теоретические вопросы. Метод векторных диаграмм; условия наблюдения интерференционной картины; когерентность световых волн; временная когерентность; пространственная когерентность; общая схема наблюдения интерференции света с использованием естественных источников; оптическая разность хода; интерференция на тонких пленках; кольца Ньютона; принцип Гюйгенса-Френеля; зоны Френеля; дифракция света на одной щели; разрешающая сила оптических приборов; критерий Релея; дифракционная решетка; главные максимумы и добавочные минимумы дифракционной решетки; разрешающая сила дифракционной решетки; угловая и линейная дисперсия; голография; дифракция рентгеновских лучей; закон Вульфа-Брэгга.

Особое внимание следует обратить на следующее. Когерентные световые волны обладают следующими свойствами: а) одинаковой частотой или длиной волны; б) одинаковой поляризацией; в) сравнимыми интенсивностями; г) постоянством разности фаз во времени.

Согласно формуле (122.3) [2], оптическая разность хода при отражении света от тонкой пленки равна

, (3.1)

где b – толщина пленки; n – абсолютный показатель преломления пленки; J₁ – угол падения света; l₀ – длина световой волны в вакууме.

При нормальном падении света на пленку sinJ₁ = 0 и оптическая разность хода становится равной

D = 2bn – l₀/2. (3.2)

Дифракция – это отклонение распространения света от прямолинейного направления и проникновение его в область геометрической тени.

В соответствии с формулой (127.5) [2] радиус m-й зоны Френеля для сферической волны равен

, (3.3)

где a – расстояние от источника до фронта волны; b – расстояние от фронта волны до точки наблюдения; l – длина волны.

В случае плоской волны можно считать, что a → ∞. Тогда для радиуса m-й зоны Френеля получаем

. (3.4)

Таблица 3

Вопросы для самоконтроля	Справочный материал
1 Что такое интерференция?	§119 [2]
2 Как методом векторных диаграмм найти амплитуду суммарного колебания при сложении колебаний одинаковой частоты?	§55 [1], §119 [2]
3 Каковы условия когерентности световых волн?	Данное пособие
4 Почему волны, испущенные независимыми естественными источниками, не являются когерентными?	§119 [2]
5 Как получить когерентные световые волны с использованием естественных источников?	§119 [2]
6 Что такое оптическая разность хода?	§119 [2]
7 Запишите условия интерференционных минимумов и максимумов.	§119 [2]
8 Что такое время когерентности?	§120 [2]
9 Что такое длина когерентности (длина цуга)?	§120 [2]
10 Каким образом происходит интерференция света при его отражении от тонких пленок?	§122 [2]
11 Чему равна оптическая разность хода при интерференции на тонких пленках?	§122 [2] и данное пособие
12 Какой должна быть толщина пленки, чтобы при отражении от нее солнечного света наблюдалась интерференция?	§122 [2]
13 Как образуются кольца Ньютона?	§122 [2]
14 Чему равны радиусы светлых и темных колец Ньютона?	§122 [2]
15 Что такое дифракция света?	Данное пособие

Окончание табл. 3

16 В чем заключается принцип Гюйгенса-Френеля?	§126 [2]
17 Что такое зоны Френеля?	§127 [2]
18 Чему равны радиусы зон Френеля?	§127 [2] и данное пособие
19 Что такое зонная пластинка?	§127 [2]
20 Запишите формулу для дифракционных минимумов при дифракции света на щели.	§129 [2]
21 Как соотносятся интенсивности нулевого, первого, второго и т.д. максимумов при дифракции света на щели?	§129 [2]
22 Сформулируйте критерий Релея для оптических приборов.
23 Как найти разрешающую силу объектива?	§132 [2]
24 Что такое дифракционная решетка?	§130 [2]
25 Что такое период дифракционной решетки?	§130 [2]
26 Запишите формулу для главных максимумов дифракционной решетки.	§130 [2]
27 Почему дифракционная решетка является спектральным прибором?	§130 [2]
28 Запишите формулу для добавочных минимумов дифракционной решетки.	§130 [2]
29 Что такое угловая и линейная дисперсия?	§130 [2]
30 Что такое разрешающая сила спектрального прибора?	§130 [2]
31 Чем определяется разрешающая сила дифракционной решетки?	§130 [2]
32 Каким образом происходит дифракция рентгеновских лучей?	§131 [2]
33 Сформулируйте закон Вульфа-Брэгга.	§131 [2]

Задачи

3.1 Найти амплитуду суммарного колебания при сложении колебаний E₁ = 3cos(w t – p/6) (В/м) и E₂ = 4cos(w t + p/3) (В/м).

3.2 Найти амплитуду суммарного колебания при сложении колебаний E₁ = 4cos(w t + p/3) (В/м) и E₂ = 4cos(w t + p) (В/м).

3.3 Определите амплитуду суммарного колебания при сложении двух колебаний одинаковой частоты: E₁ = sinw t; E₂ = 4cosw t (В/м).

3.4 Минимальная разность хода двух когерентных волн, при которой наблюдается минимум интенсивности, равна 300 нм. Чему равна длина волны?

3.5 На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l = 500 нм. Отраженный свет максимально усилен вследствие интерференции. Показатель преломления пленки n = 1, 4. Определить минимальную толщину пленки.

3.6 На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l = 500 нм. Пленка нанесена на стекло с показателем преломления 1, 5. Отраженный от пленки свет максимально усилен вследствие интерференции. Показатель преломления пленки 1, 4. Определить минимальную толщину пленки.

3.7 Чему равен номер темного кольца при наблюдении колец Ньютона в отраженном свете, если радиус этого кольца 4 мм, длина волны 500 нм, а радиус кривизны линзы 2 м?

3.8 Чему равен радиус 9-го темного кольца Ньютона при наблюдении интерференционной картины в отраженном свете, если длина световой волны 500 нм, а радиус кривизны линзы 2 м?

3.9 Чему равен радиус четвертой зоны Френеля, если длина световой волны 500 нм, а расстояние до точки наблюдения 2 м?

3.10 Радиус второй зоны Френеля равен 4 мм. Чему равна длина световой волны, если расстояние до точки наблюдения 10 м?

3.11 Площади зон Френеля равны 3, 14 мм². Чему равно расстояние до точки наблюдения, если длина световой волны 500 нм?

3.12 Площади зон Френеля равны 3, 14 мм². Чему равна длина световой волны, если расстояние до точки наблюдения 2, 5 м?

3.13 Как будет выглядеть векторная диаграмма, если открыто 1, 5 зоны Френеля?

3.14 Нарисуйте векторную диаграмму, если открыты вторая, третья и пятая зоны Френеля.

3.15 На пути плоской волны поместили экран с отверстиями, соответствующими 1-й и 3-й зонам Френеля. Во сколько раз изменится интенсивность в точке наблюдения?

3.16 Нарисуйте векторную диаграмму для первого максимума при дифракции света на щели.

3.17 Нарисуйте векторную диаграмму для второго минимума при дифракции света на щели.

3.18 Чему равна ширина щели, если при дифракции света с длиной волны 400 нм на ней четвертый дифракционный минимум наблюдается при угле отклонения 30°. Чему равна длина световой волны?

3.19 Третий дифракционный минимум при дифракции света на щели шириной 4, 8 мкм наблюдается при угле отклонения 30°. Чему равна длина волны?

3.20 Чему равна расходимость светового пучка с длиной волны 500 нм при дифракции на отверстии диаметром 10 мкм?

3.21 При дифракции света на отверстии диаметром 20 мкм расходимость светового пучка равна 0, 04 рад. Чему равна длина волны?

3.22 Определите постоянную дифракционной решетки, если максимум первого порядка света длины волны 500 нм наблюдается под углом 30°.

3.23 Нарисуйте векторную диаграмму для первого дополнительного минимума в случае дифракционной решетки, состоящей из 5 щелей.

3.24 Чему равен порядок главного максимума при дифракции света с длиной волны 400 нм на решетке с периодом 3, 2 мкм, если угол отклонения света равен 30°?

3.25 При дифракции света на решетке с периодом 5 мкм пятый главный максимум наблюдается при угле отклонения 30°. Чему длина световой волны?

3.26 Разрешающая сила дифракционной решетки для третьего главного максимума равна 18000. Чему равно число щелей решетки?

3.27 Чему равно межплоскостное расстояние в кристалле, если при дифракции рентгеновских лучей с длиной волны 0, 2 нм дифракционный максимум первого порядка наблюдается для угла 30°?

Квантовая оптика

Теоретические вопросы. Тепловое излучение; поглощательная способность; абсолютно черное тело; испускательная способность; энергетическая светимость; спектр абсолютно черного тела; закон Стефана-Больцмана; закон смещения Вина; закон Кирхгофа; ультрафиолетовая катастрофа; гипотеза Планка; фотоэффект; законы фотоэффекта; формула Эйнштейна для фотоэффекта; опыт Боте; корпускулярно-волновой дуализм; фотоны; эффект Комптона.

Особое внимание следует обратить на следующее. Экспериментально установлены следующие законы фотоэффекта: 1) число вырываемых электронов пропорционально интенсивности света; 2) скорость вырываемых электронов не зависит от интенсивности света, а зависит лишь от его частоты; 3) существует граничная частота падающего излучения ν ₀ (красная граница фотоэффекта), такая, что при ν < ν ₀ фотоэффект прекращается.

Таблица 4

Вопросы для самоконтроля	Справочный материал
1 Что такое тепловое излучение?	§1 [3]
2 Что такое поглощательная способность?	§2 [3]
3 Что такое абсолютно черно тело?	§2 [3]
4 Что такое испускательная способность?	§2 [3]
5 Что такое энергетическая светимость?	§2 [3]
6 Как выглядит типичный спектр абсолютно черного тела?	§2 [3]
7 Сформулируйте закон Стефана-Больцмана.	§4 [3]
8 Сформулируйте закон смещения Вина.	§4 [3]
9 Что такое ультрафиолетовая катастрофа?	§6 [3]
10 В чем заключается гипотеза Планка?	§7 [3]
11 Что такое фотоэффект?	§9 [3]
12 Сформулируйте законы фотоэффекта.	Данное пособие
13 Что такое красная граница фотоэффекта?	§9 [3] и данное пособие
14 Как Эйнштейн объяснил законы фотоэффекта?	§9 [3]
15 Что доказал опыт Боте?	§10 [3]
16 Чему равна энергия фотона?	§10 [3]
17 Чему равен импульс фотона?	§10 [3]
18 Что такое корпускулярно-волновой дуализм?	§10 [3]
19 В чем состоит эффект Комптона?	§11 [3]
20 Что такое комптоновская длина волны?	§11 [3]
21 Как найти длину волны рассеянного рентгеновского излучения?	§11 [3]

Задачи

4.1 Во сколько раз увеличится энергетическая светимость тела, если его абсолютную температуру увеличить в два раза?

4.2 Абсолютно черное тело имеет температуру 500 К. Какова будет температура тела, если в результате нагревания поток излучения увеличится в 16 раз?

4.3 Как и во сколько раз изменится температура абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (l₁ = 780 нм) на фиолетовую (l₂ = 390 нм)?

4.4 Вычислить энергию, излучаемую за 1 мин с площади 1 см² абсолютно черного тела, температура которого 1000 К (s = 5, 67·10^–8 Вт/м²К⁴).

4.5 Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, равна 0, 6 мкм. Определить температуру тела (b = = 0, 0029 м·К).

4.6 Температура абсолютно черного тела 2000 К. Определить длину волны, на которую приходится максимум энергии излучения (b = 0, 0029 м·К).

4.7 Длина волны излучения увеличилась в 2 раза. Во сколько раз изменилась энергия фотонов?

4.8 На поверхность металла падает поток фотонов с энергией 10 эВ. Красная граница фотоэффекта данного металла 4 эВ. На сколько нужно увеличить энергию фотонов, чтобы кинетическая энергия фотоэлектронов увеличилась в 2 раза?

4.9 На поверхность металла падают монохроматические лучи с длиной волны l = 0, 1 мкм. Красная граница фотоэффекта l₀ = 0, 3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?

4.10 Минимальная энергия фотона, вызывающего фотоэффект, равна 3 эВ. Во сколько раз возрастет кинетическая энергия фотоэлектрона, если энергия фотона, вызывающего фотоэффект, изменится от 5 до 9 эВ?

4.11 При облучении металлической пластинки светом с энергией фотонов 8 эВ максимальная энергия фотоэлектронов равна 6 эВ. Какова будет максимальная энергия фотоэлектронов, если эту же пластинку облучать светом с энергией фотонов, равной 10 эВ?

4.12 Минимальная энергия фотона, вызывающего фотоэффект, равна 2 эВ. Какова будет энергия фотона, вызывающего фотоэффект, если кинетическая энергия фотоэлектрона равна 6 эВ?

Атомная физика

Теоретические вопросы. Закономерности в атомных спектрах; формула Бальмера; модель атома Томсона; ядерная модель атома; постулаты Бора; гипотеза де Бройля; определенные и неопределенные состояния и события; недетерминированные события и состояния; опыт по интерференции электронов на двух щелях; амплитуда вероятности; принципы квантовой механики; бозе- и ферми-частицы; рассеяние тождественных частиц; принцип запрета Паули; базисные состояния; уравнения движения; гамильтонова матрица; стационарные состояния; уравнение Шредингера; волновая функция; решение уравнения Шредингера для свободной частицы; графическое решение уравнения Шредингера; локализованные состояния в потенциальной яме; квантование энергии; туннельный эффект; принцип неопределенности Гейзенберга; квантование момента импульса; азимутальное и магнитное квантовые числа; решение уравнения Шредингера для атома водорода; главное квантовое число; спин электрона; спин-орбитальное взаимодействие; периодическая система элементов.

Особое внимание следует обратить на следующее. В физике микромира появляется качественно новый класс состояний и событий, не существовавших в классической физике: недетерминированные состояния и события. В классической физике существуют определенные и неопределенные состояния и события. В случае определенных состояний мы можем точно сказать, что происходит с наблюдаемым объектом. В случае неопределенных состояний мы точно не знаем, что происходит с объектом, но при желании можем это узнать.

Например, если есть частица, которая может находиться в одной из трех ячеек, и мы точно знаем, в какой именно она находится, то это определенное состояние. Если же мы точно не знаем, в какой ячейке находится частица, но при желании можем узнать, например, осветив поочередно ячейки пучком фотонов и регистрируя рассеянные частицей фотоны, то это неопределенное состояние. Если же нет никакой возможности зафиксировать частицу даже с помощью фотонов, то мы приходим к понятию недетерминированного состояния. Иными словами, если исключить возможность взаимодействия частицы с окружающей средой, то она будет находиться в недетерминированном состоянии.

Например, чтобы доказать существование орбиты у электрона в атоме, электрон надо зафиксировать в нескольких точках его орбиты с помощью рассеянных фотонов. Для этого надо использовать свет с длиной волны как минимум в 10 раз меньшей размеров атома, т.е. порядка 10^–11 м. Энергия таких фотонов в тысячи раз превосходит энергию ионизации валентных электронов. Поэтому при столкновении с фотоном такой энергии электрон будет выброшен за пределы атома, и обнаружить его в следующей точке траектории не будет никакой возможности. Таким образом, состояние электрона в атоме – это пример недетерминированного состояния.

Событие – это переход системы из одного состояния в другое. События также подразделяются на определенные, неопределенные и недетерминированные. В случае определенного события мы точно знаем, каким способом система перешла из одного состояния в другое. В случае неопределенного события нам неизвестно, каким способом система перешла из одного состояния в другое, но при желании мы можем это узнать.

Например, человек может попасть из пункта А в пункт B через перевал 1 или через перевал 2. Если известно точно, через какой перевал прошел человек, то это определенное событие. Если неизвестно, через какой перевал прошел человек, то это неопределенное событие. Так же, как и в случае с состояниями, неопределенное событие при желании можно сделать определенным. В данном случае человек может либо сам предъявить доказательства своего маршрута (отметки на траектории) или это может сделать посторонний наблюдатель, предъявив фотографии, сделанные скрытой камерой.

В случае макрообъектов (каким является человек) неопределенное событие всегда можно сделать определенным, поскольку макрообъект обязательно рассеивает электромагнитное излучение (солнечный свет, космические лучи и т.д.). Совсем иная ситуация наблюдается в микромире.

Рассмотрим, например, эксперимент на интерференцию электронов на двух щелях, схема которого представлена на рис. 5.1. На этом рисунке П – электронная пушка (источник монохроматических электронов); Э – непрозрачный экран с двумя одинаковыми щелями 1 и 2; за экраном помещена фотопластинка Фп, регистрирующая попадающие на нее электроны. В том случае, если между источником электронов и экраном с фотопластинкой нет никаких фотонов, нет никакой возможности узнать, через какую щель прошел электрон. В этом случае мы имеем дело с недетерминированным событием, и на фотопластинке после обработки будет наблюдаться отчетливая интерференционная картина для вероятности попадания электрона P₁₂ (рис. 5.1, а).

Если же между источником электронов и фотопластинкой обеспечить достаточно высокую плотность фотонов, чтобы каждый электрон, прошедший через щель 1 или 2 обязательно рассеивал фотон, результат эксперимента существенно изменится: вместо интерференционной картины мы будем наблюдать простую сумму вероятностей прохождения электрона через каждую щель отдельно. На рис. 5.1, б представлена вероятность регистрации электрона при открытой только щели 1 (P₁) или только щели 2 (P₂), а на рис. 5.1, в – сумма вероятностей P₁ + P₂. При этом неважно, будем ли мы регистрировать рассеянные

фотоны (определенное событие) или нет (неопределенное событие).

Для работы с недетерминированными событиями в квантовой механике вводятся три принципа. Первый принцип заключается в том, что каждое событие микромира характеризуется амплитудой вероятности F, квадрат модуля которой дает вероятность данного события:

P = |F|² = F*F. (5.1)

Второй принцип: если сложное событие состоит из нескольких простых событий, то его амплитуда F_с равна произведению амплитуд простых событий F_i:

F_с = F₁·F₂·F₃·...·F_N. (5.2)

Третий принцип (принцип суперпозиции). Если событие может произойти несколькими независимыми способами, причем не имеется никакой возможности выяснить, каким именно способом произошло событие (недетерминированное событие), то результирующая амплитуда этого события F равна сумме амплитуд этого события для каждого способа (F_i):

. (5.3)

Если же возможно, в принципе, выяснить, каким именно способом произошло событие (неопределенное событие), то вероятность этого события P равна сумме вероятностей этого события для каждого способа (P_i):

. (5.4)

Например, в упомянутом эксперименте на прохождение электронов через две щели мы имеем дело либо с неопределенным или определенным событием (при достаточно высокой плотности фотонов между источником электронов и фотопластинкой), либо с недетерминированным событием (если между источником электронов и фотопластинкой фотоны отсутствуют). В первом случае вероятность регистрации электрона равна

P₁₂ = P₁ + P₂, (5.5)

и мы будем иметь вероятность регистрации электронов, изображенную на рис. 5.1, в.

Во втором случае амплитуда вероятности регистрации электрона равна

F₁₂ = F₁ + F₂, (5.6)

где F₁ и F₂ – амплитуды вероятности прохождения электронов через щель 1 и 2 соответственно. Тогда вероятность регистрации электрона в соответствии с первым принципом будет равна

. (5.7)

Последние два слагаемых в (5.7) называются интерференционными, в них заключено отличие вероятности (5.5) от (5.7). В том случае, когда сумма интерференционных слагаемых равна с обратным знаком P₁ + P₂, вероятность регистрации электронов будет равна нулю. В том случае, когда сумма интерференционных слагаемых равна P₁ + P₂, вероятность регистрации электронов будет в два раза больше, чем сумма вероятностей при открытой сначала первой, а затем второй щели. В результате мы будем иметь вероятность регистрации электронов, изображенную на рис. 5.1, а.

Если же плотность фотонов между источником электронов и фотопластинкой будет недостаточна для их рассеяния на каждом электроне, мы будем иметь промежуточную картину почернения фотопластинки между изображенными на рис. 5.1, а и 5.1, в. И при увеличении плотности фотонов мы будем наблюдать плавный переход от распределения, изображенного на рис. 5.1, а, к распределению, изображенному на рис. 5.1, в.

Зависящее от времени уравнение Шредингера для микрочастицы массы m имеет вид:

, (5.8)

где i – мнимая единица, ћ – постоянная Планка " h с чертой", связанная с обычной постоянной h соотношением ћ = h/2p; Y – волновая функция (пси-функция); U(x, y, z) – потенциальная энергия частицы.

В случае стационарного состояния

, (5.9)

где E – энергия частицы.

Подставляя функцию (5.9) в уравнение (5.8), получаем уравнение Шредингера для стационарных состояний:

. (5.10)

Для одномерного случая уравнение (5.10) превращается в одномерное уравнение Шредингера для стационарных состояний:

. (5.11)

Для свободной частицы U(x) = 0 и вместо (5.11) имеем

. (5.12)

Решением этого уравнения является функция

, (5.13)

где k – волновое число, связанное с длиной волны l частицы соотношением k = 2p/l.

При подстановке функции (5.13) в (5.12) для кинетической энергии получаем

. (5.14)

Из формулы (5.14) видно, что кинетическая энергия обратно пропорциональна квадрату длины волны частицы. На рис. 5.2 изображены мнимые части волновых функций свободной частицы с кинетическими энергиями E = E₀/4, E₀ и 4E₀ соответственно.

В том случае, если потенциальная энергия частицы не равна нулю, но является постоянной величиной (U(x) = const), можно ввести обозначение E_кин = = E – U, и снова прийти к уравнению (5.12) с энергией E_кин вместо E.

Таблица 5

⇐ Предыдущая 1 23