D.3. Системы эконометрических уравнений
Рассмотрим пример. Изучается модель вида

где  – расходы на потребление в период – расходы на потребление в период  , ,  – совокупный доход в период – совокупный доход в период  , , 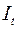 – инвестиции в период – инвестиции в период  , , 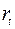 – процентная ставка в период – процентная ставка в период  , , 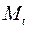 – денежная масса в период – денежная масса в период  , , 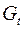 – государственные расходы в период – государственные расходы в период  , , 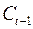 – расходы на потребление в период – расходы на потребление в период  , , 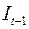 инвестиции в период инвестиции в период  . Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода. . Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.
Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные  и четыре предопределенные переменные (две экзогенные переменные – и четыре предопределенные переменные (две экзогенные переменные – 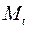 и и 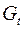 и две лаговые переменные – и две лаговые переменные – 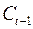 и и 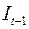 ). ).
Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое уравнение:  . Это уравнение содержит две эндогенные переменные . Это уравнение содержит две эндогенные переменные  и и  и одну предопределенную переменную и одну предопределенную переменную 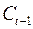 . Таким образом, . Таким образом,  , а , а  , т.е. выполняется условие , т.е. выполняется условие  . Уравнение сверхидентифицируемо. . Уравнение сверхидентифицируемо.
Второе уравнение:  . Оно включает две эндогенные переменные . Оно включает две эндогенные переменные 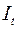 и и 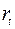 и одну экзогенную переменную и одну экзогенную переменную 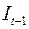 . Выполняется условие . Выполняется условие 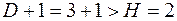 . Уравнение сверхидентифицируемо. . Уравнение сверхидентифицируемо.
Третье уравнение:  . Оно включает две эндогенные переменные . Оно включает две эндогенные переменные  и и 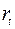 и одну экзогенную переменную и одну экзогенную переменную 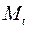 . Выполняется условие . Выполняется условие 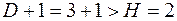 . Уравнение сверхидентифицируемо. . Уравнение сверхидентифицируемо.
Четвертое уравнение:  . Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет. . Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
|
| 
| 
| 
| 
| 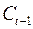
| 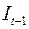
| 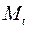
| 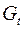
| | I уравнение
| –1
|
|
| 
| 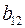
|
|
|
| | II уравнение
|
| –1
| 
|
|
| 
|
|
| | III уравнение
|
|
| –1
| 
|
|
| 
|
| | Тождество
|
|
|
| –1
|
|
|
|
| В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
| 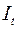
| 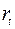
| 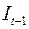
| 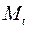
| 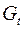
| | II уравнение
| –1
| 
| 
|
|
| | III уравнение
|
| –1
|
| 
|
| | Тождество
|
|
|
|
|
| Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 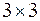 не равен нулю: не равен нулю:
 . .
Достаточное условие идентификации для данного уравнения выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
| 
| 
| 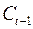
| 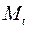
| 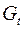
| | I уравнение
| –1
| 
| 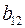
|
|
| | III уравнение
|
| 
|
| 
|
| | Тождество
|
| –1
|
|
|
| Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 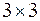 не равен нулю: не равен нулю:
 . .
Достаточное условие идентификации для данного уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
| 
| 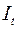
| 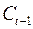
| 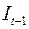
| 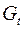
| | I уравнение
| –1
|
| 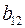
|
|
| | II уравнение
|
| –1
|
| 
|
| | Тождество
|
|
|
|
|
| Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 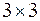 не равен нулю: не равен нулю:
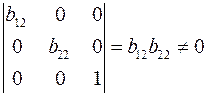 . .
Достаточное условие идентификации для данного уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом:

Варианты индивидуальных заданий
Даны системы эконометрических уравнений.
Требуется
1. Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2. Определите метод оценки параметров модели.
3. Запишите в общем виде приведенную форму модели.
Вариант 1
Модель протекционизма Сальватора (упрощенная версия):

где 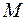 – доля импорта в ВВП; – доля импорта в ВВП;  – общее число прошений об освобождении от таможенных пошлин; – общее число прошений об освобождении от таможенных пошлин; 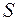 – число удовлетворенных прошений об освобождении от таможенных пошлин; – число удовлетворенных прошений об освобождении от таможенных пошлин;  – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет; – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;  – реальный ВВП; – реальный ВВП;  – реальный объем чистого экспорта; – реальный объем чистого экспорта;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 2
Макроэкономическая модель (упрощенная версия модели Клейна):

где  – потребление; – потребление; 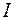 – инвестиции; – инвестиции;  – доход; – доход;  – налоги; – налоги; 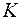 – запас капитала; – запас капитала;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 3
Макроэкономическая модель экономики США (одна из версий):

где  – потребление; – потребление;  – ВВП; – ВВП; 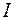 – инвестиции; – инвестиции;  – процентная ставка; – процентная ставка; 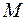 – денежная масса; – денежная масса;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 4
Модель Кейнса (одна из версий):

где  – потребление; – потребление;  – ВВП; – ВВП; 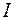 – валовые инвестиции; – валовые инвестиции;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 5
Модель денежного и товарного рынков:

где  – процентные ставки; – процентные ставки;  – реальный ВВП; – реальный ВВП; 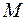 – денежная масса; – денежная масса; 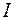 – внутренние инвестиции; – внутренние инвестиции;  – реальные государственные расходы. – реальные государственные расходы.
Вариант 6
Модифицированная модель Кейнса:

где  – потребление; – потребление;  – доход; – доход; 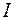 – инвестиции; – инвестиции;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 7
Макроэкономическая модель:

где  – расходы на потребление; – расходы на потребление;  – чистый национальный продукт; – чистый национальный продукт;  – чистый национальный доход; – чистый национальный доход; 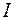 – инвестиции; – инвестиции;  – косвенные налоги; – косвенные налоги;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
Вариант 8
Гипотетическая модель экономики:

где  – совокупное потребление в период – совокупное потребление в период  ; ;  – совокупный доход в период – совокупный доход в период  ; ;  – инвестиции в период – инвестиции в период  ; ;  – налоги в период – налоги в период  ; ;  – государственные доходы в период – государственные доходы в период  . .
Вариант 9
Модель денежного рынка:

где  – процентные ставки; – процентные ставки;  – ВВП; – ВВП; 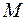 – денежная масса; – денежная масса; 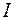 – внутренние инвестиции. – внутренние инвестиции.
Вариант 10
Конъюнктурная модель имеет вид:

где  – расходы на потребление; – расходы на потребление;  – ВВП; – ВВП; 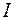 – инвестиции; – инвестиции;  – процентная ставка; – процентная ставка; 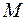 – денежная масса; – денежная масса;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период.
D.4. Временные ряды
Рассмотрим пример. Пусть имеются некоторые условные данные об общем количестве правонарушений на таможне одного из субъектов РФ (например, Республики Татарстан).
Таблица 4.1
| Год
| Квартал
| 
| Количество возбужденных дел, 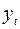
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| |
| I
|
|
| | II
|
|
| | III
|
|
| | IV
|
|
| Построим поле корреляции:

Рис. 4.4.
Уже исходя из графика видно, что значения  образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу. образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу.
Таблица 4.2

| 
| 
| 
| 
| 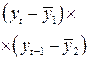
| 
| 
| |
|
|
|
|
|
|
|
| |
|
| –
| –
| –
| –
| –
| –
| |
|
|
| -328, 33
| -288, 13
| 94601, 72
| 107800, 59
| 83018, 90
| |
|
|
| 169, 67
| -292, 13
| -49565, 70
| 28787, 91
| 85339, 94
| |
|
|
| 315, 67
| 205, 87
| 64986, 98
| 99647, 55
| 42382, 46
| |
|
|
| -342, 33
| 351, 87
| -120455, 66
| 117189, 83
| 123812, 50
| |
|
|
| -228, 33
| -306, 13
| 69898, 66
| 52134, 59
| 93715, 58
| |
|
|
| 292, 67
| -192, 13
| -56230, 69
| 85655, 73
| 36913, 94
| |
|
|
| 320, 67
| 328, 87
| 105458, 74
| 102829, 25
| 108155, 48
| |
|
|
| -309, 33
| 356, 87
| -110390, 60
| 95685, 05
| 127356, 20
| |
|
|
| -344, 33
| -273, 13
| 94046, 85
| 118563, 15
| 74600, 00
| |
|
|
| 292, 67
| -308, 13
| -90180, 41
| 85655, 73
| 94944, 10
| |
|
|
| 205, 67
| 328, 87
| 67638, 69
| 42300, 15
| 108155, 48
| |
|
|
|
|
|
|
|
| |
|
|
| -238, 33
| 241, 87
| -57644, 88
| 56801, 19
| 58501, 10
| |
|
|
| -245, 33
| -202, 13
| 49588, 55
| 60186, 81
| 40856, 54
| |
|
|
| 220, 67
| -209, 13
| -46148, 72
| 48695, 25
| 43735, 36
| |
|
|
| 227, 67
| 256, 87
| 58481, 59
| 51833, 63
| 65982, 20
| | Сумма
|
|
| 9, 05
| 0, 05
| 74085, 16
| 1153766, 39
| 1187469, 73
| | Среднее значение
| 699, 33
| 663, 13
| –
| –
| –
| –
| –
| Следует заметить, что среднее значение получается путем деления не на 16, а на 15, т.к. у нас теперь на одно наблюдение меньше.
Теперь вычисляем коэффициент автокорреляции первого порядка по формуле
 (4.1) (4.1)
где

 . .
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка.
Таблица 4.3

| 
| 
| 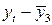
| 
| 
| 
| 
| |
|
|
|
|
|
|
|
| |
|
| –
| –
| –
| –
| –
| –
| |
|
| –
| –
| –
| –
| –
| –
| |
|
|
| 145, 57
| -269, 79
| -39273, 33
| 21190, 62
| 72786, 64
| |
|
|
| 291, 57
| -273, 79
| -79828, 95
| 85013, 06
| 74960, 96
| |
|
|
| -366, 43
| 224, 21
| -82157, 27
| 134270, 94
| 50270, 12
| |
|
|
| -252, 43
| 370, 21
| -93452, 11
| 63720, 90
| 137055, 44
| |
|
|
| 268, 57
| -287, 79
| -77291, 76
| 72129, 84
| 82823, 08
| |
|
|
| 296, 57
| -173, 79
| -51540, 90
| 87953, 76
| 30202, 96
| |
|
|
| -333, 43
| 347, 21
| -115770, 23
| 111175, 56
| 120554, 78
| |
|
|
| -368, 43
| 375, 21
| -138238, 62
| 135740, 66
| 140782, 54
| |
|
|
| 268, 57
| -254, 79
| -68428, 95
| 72129, 84
| 64917, 94
| |
|
|
| 181, 57
| -289, 79
| -52617, 17
| 32967, 66
| 83978, 24
| |
|
|
| -262, 43
| 347, 21
| -91118, 32
| 68869, 50
| 120554, 78
| |
|
|
| -269, 43
| 260, 21
| -70108, 38
| 72592, 52
| 67709, 24
| |
|
|
| 196, 57
| -183, 79
| -36127, 60
| 38639, 76
| 33778, 76
| |
|
|
| 203, 57
| -190, 79
| -38839, 12
| 41440, 74
| 36400, 82
| | Сумма
|
|
| -0, 02
| -0, 06
| -1034792, 71
| 1037835, 43
| 1116776, 36
| | Среднее значение
| 723, 43
| 644, 79
| –
| –
| –
| –
| –
| Следовательно
 . .
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу.
Таблица 4.4
| Лаг
| Коэффициент автокорреляции уровней
| |
| 0, 063294
| |
| –0, 961183
| |
| –0, 036290
| |
| 0, 964735
| |
| 0, 050594
| |
| –0, 976516
| |
| –0, 069444
| |
| 0, 964629
| |
| 0, 162064
| |
| -0, 972918
| |
| -0, 065323
| |
| 0, 985761
| Коррелограмма:
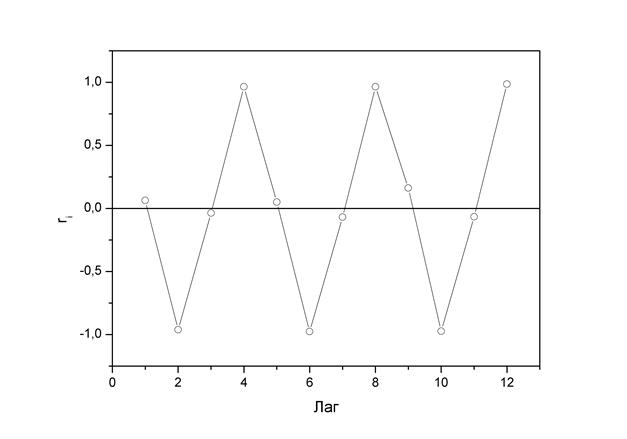
Рис. 4.5.
Анализ коррелограммы и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
2. Построение аддитивной модели временного ряда. Обратимся к данным об объеме правонарушений на таможне за четыре года, представленным в табл. 4.1.
Было показано, что данный временной ряд содержит сезонные колебания периодичностью 4, т.к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 4.5).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 4.5). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 4.5).
Таблица 4.5
№ квартала,

| Количество правонарушений,
| Итого за четыре квартала
| Скользящая средняя за четыре квартала
| Центрированная скользящая средняя
| Оценка сезонной компоненты
| |
|
|
|
|
|
| |
|
| –
| –
| –
| –
| |
|
|
| 657, 5
| –
| –
| |
|
|
|
| 655, 25
| 213, 75
| |
|
|
|
| 665, 5
| 349, 5
| |
|
|
| 708, 75
| 693, 75
| -336, 75
| |
|
|
|
| 709, 375
| -238, 375
| |
|
|
| 718, 25
| 714, 125
| 277, 875
| |
|
|
| 689, 25
| 703, 75
| 316, 25
| |
|
|
| 689, 25
| 689, 25
| -299, 25
| |
|
|
| 660, 5
| 674, 875
| -319, 875
| |
|
|
| 678, 25
| 669, 375
| 322, 625
| |
|
|
|
| 690, 625
| 214, 375
| |
|
|
|
|
| -233
| |
|
|
| 690, 5
| 687, 75
| -233, 75
| |
|
| –
| –
| –
| –
| |
|
| –
| –
| –
| –
| Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 4.5). Используем эти оценки для расчета значений сезонной компоненты  (табл. 4.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты (табл. 4.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты  . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 4.6
| Показатели
| Год
| № квартала, 
| | I
| II
| III
| IV
| |
|
| –
| –
| 213, 75
| 349, 5
| |
| -336, 75
| -238, 375
| 277, 875
| 316, 25
| |
| -299, 25
| -319, 875
| 322, 625
| 214, 375
| |
| -233
| -233, 75
| –
| –
| Всего за  -й квартал -й квартал
|
| -869
| -792
| 814, 25
| 880, 125
| Средняя оценка сезонной компоненты для  -го квартала, -го квартала, 
|
| -289, 667
| -264
| 271, 417
| 293, 375
| Скорректированная сезонная компонента, 
|
| -292, 448
| -266, 781
| 268, 636
| 290, 593
| Для данной модели имеем:
 . .
Корректирующий коэффициент:  . .
Рассчитываем скорректированные значения сезонной компоненты (  ) и заносим полученные данные в таблицу 4.6. ) и заносим полученные данные в таблицу 4.6.
Проверим равенство нулю суммы значений сезонной компоненты:
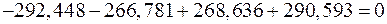 . .
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины  (гр. 4 табл. 4.7). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту. (гр. 4 табл. 4.7). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Таблица 4.7

| 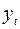
| 
| 
| 
| 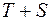
| 
| 
| |
|
|
|
|
|
|
|
| |
|
| -292, 448
| 667, 448
| 672, 700
| 380, 252
| -5, 252
| 27, 584
| |
|
| -266, 781
| 637, 781
| 673, 624
| 406, 843
| -35, 843
| 1284, 721
| |
|
| 268, 636
| 600, 364
| 674, 547
| 943, 183
| -74, 183
| 5503, 117
| |
|
| 290, 593
| 724, 407
| 675, 470
| 966, 063
| 48, 937
| 2394, 830
| |
|
| -292, 448
| 649, 448
| 676, 394
| 383, 946
| -26, 946
| 726, 087
| |
|
| -266, 781
| 737, 781
| 677, 317
| 410, 536
| 60, 464
| 3655, 895
| |
|
| 268, 636
| 723, 364
| 678, 240
| 946, 876
| 45, 124
| 2036, 175
| |
|
| 290, 593
| 729, 407
| 679, 163
| 969, 756
| 50, 244
| 2524, 460
| |
|
| -292, 448
| 682, 448
| 680, 087
| 387, 639
| 2, 361
| 5, 574
| |
|
| -266, 781
| 621, 781
| 681, 010
| 414, 229
| -59, 229
| 3508, 074
| |
|
| 268, 636
| 723, 364
| 681, 933
| 950, 569
| 41, 431
| 1716, 528
| |
|
| 290, 593
| 614, 407
| 682, 857
| 973, 450
| -68, 450
| 4685, 403
| |
|
| -292, 448
| 753, 448
| 683, 780
| 391, 332
| 69, 668
| 4853, 630
| |
|
| -266, 781
| 720, 781
| 684, 703
| 417, 922
| 36, 078
| 1301, 622
| |
|
| 268, 636
| 651, 364
| 685, 627
| 954, 263
| -34, 263
| 1173, 953
| |
|
| 290, 593
| 636, 407
| 686, 550
| 977, 143
| -50, 143
| 2514, 320
| Шаг 4. Определим компоненту  данной модели. Для этого проведем аналитическое выравнивание ряда ( данной модели. Для этого проведем аналитическое выравнивание ряда (  ) с помощью линейного тренда. Результаты аналитического выравнивания следующие: ) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
 . .
Подставляя в это уравнение значения  , найдем уровни , найдем уровни  для каждого момента времени (гр. 5 табл. 4.7). для каждого момента времени (гр. 5 табл. 4.7).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням  значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 4.7). значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 4.7).
На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Рис. 4.6.
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
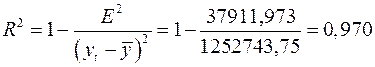 . .
Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.
Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года. Прогнозное значение  уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
 . .
Получим
 ; ;
 . .
Значения сезонных компонент за соответствующие кварталы равны:  и и  . Таким образом, . Таким образом,
 ; ;
 . .
Т.е. в первые два квартала 2003 г. следовало ожидать порядка 395 и 422 правонарушений соответственно.
Построение мультипликативной модели рассмотрим на данных предыдущего примера.
Шаг 1. Методика, применяемая на этом шаге, полностью совпадает с методикой построения аддитивной модели.
Таблица 4.8
№ квартала,

| Количество правонарушений,

| Итого за четыре квартала
| Скользящая средняя за четыре квартала
| Центрированная скользящая средняя
| Оценка сезонной компоненты
| |
|
|
|
|
|
| |
|
| –
| –
| –
| –
| |
|
|
| 657, 5
| –
| –
| |
|
|
|
| 655, 25
| 1, 3262
| |
|
|
|
| 665, 5
| 1, 5252
| |
|
|
| 708, 75
| 693, 75
| 0, 5146
| |
|
|
|
| 709, 375
| 0, 6640
| |
|
|
| 718, 25
| 714, 125
| 1, 3891
| |
|
|
| 689, 25
| 703, 75
| 1, 4494
| |
|
|
| 689, 25
| 689, 25
| 0, 5658
| |
|
|
| 660, 5
| 674, 875
| 0, 5260
| |
|
|
| 678, 25
| 669, 375
| 1, 4820
| |
|
|
|
| 690, 625
| 1, 3104
| |
|
|
|
|
| 0, 6643
| |
|
|
| 690, 5
| 687, 75
| 0, 6601
| |
|
| –
| –
| –
| –
| |
|
| –
| –
| –
| –
| Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 4.8). Эти оценки используются для расчета сезонной компоненты 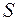 (табл. 4.9). Для этого найдем средние за каждый квартал оценки сезонной компоненты (табл. 4.9). Для этого найдем средние за каждый квартал оценки сезонной компоненты  . Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4. . Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 4.9
| Показатели
| Год
| № квартала, 
| | I
| II
| III
| IV
| |
|
| –
| –
| 1, 3262
| 1, 5252
| |
| 0, 5146
| 0, 6640
| 1, 3891
| 1, 4494
| |
| 0, 5658
| 0, 5260
| 1, 4820
| 1, 3104
| |
| 0, 6643
| 0, 6601
| –
| –
| Всего за  -й квартал -й квартал
|
| 1, 7447
| 1, 8501
| 4, 1973
| 4, 2850
| Средняя оценка сезонной компоненты для  -го квартала, -го квартала, 
|
| 0, 5816
| 0, 6167
| 1, 3991
| 1, 4283
| Скорректированная сезонная компонента, 
|
| 0, 5779
| 0, 6128
| 1, 3901
| 1, 4192
| Имеем
 . .
Определяем корректирующий коэффициент:
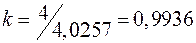 . .
Скорректированные значения сезонной компоненты  получаются при умножении ее средней оценки получаются при умножении ее средней оценки  на корректирующий коэффициент на корректирующий коэффициент  . .
Проверяем условие равенство 4 суммы значений сезонной компоненты:
 . .
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины  (гр. 4 табл. 4.10), которые содержат только тенденцию и случайную компоненту. (гр. 4 табл. 4.10), которые содержат только тенденцию и случайную компоненту.
Таблица 4.10
Популярное:
|

