
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Глава 3.Основы электродинамикиСтр 1 из 6Следующая ⇒
Глава 3.Основы электродинамики Предметом изучения электродинамики являетсяэлектромагнитное взаимодействие тел, обусловленное наличием в составе атомов вещества элементарных частиц, обладающих особым свойством, называемым«электрический заряд». Электромагнитное взаимодействие проявляется в виде сил притяжения или отталкивания. В результате действия этих силможет изменяться пространственное распределение заряженных частиц, возникать деформация и механическое движение тел. Среди известных типов физических взаимодействий электромагнитное отличается наибольшим разнообразием своих проявлений: оно ответственно за возникновение сил упругости и трения, оно приводит к ряду специфических, тепловых, химических, оптических и механических эффектов. Электромагнитными взаимодействиями обусловлена структура материи в областях пространственных масштабов от 10-14 до 105м (на меньших расстояниях более важны ядерные взаимодействия, а на больших – гравитационные). Электромагнитные процессы играют главную роль в развитии современной техники (энергетики, транспорта, связи) Общие понятия Термин «электрический заряд»используется в трех смыслах: как свойство частиц и тел, как физическая величина и как обозначение идеализированной модели заряженных тел. Электрический заряд–это свойство элементарных частиц вещества, благодаря которому они способны к особого рода взаимодействию, проявляющемуся в действии сил притяжения или отталкивания. Электрический заряд частицы нельзя увеличить, уменьшить, снять или сообщить – это неотъемлемое свойство частицы, подобное массе.Электрический заряд – это биполярное свойство. Бывают положительные и отрицательные заряды. Присвоение зарядам знаков + и - выражает тот факт, что при соединении объектов, обладающих зарядами противоположной полярности, происходит компенсация зарядов так, что получившаяся система не будет проявлять электрических свойств.Одноименные (однополярные) заряды отталкиваются, разноименные (разнополярные) ‒ притягиваются. Электрический зарядq – скалярная физическая величина, определяющая интенсивность электромагнитного взаимодействия заряженных тел или частиц. При статических проявлениях определяется по силовому взаимодействию на основе закона Кулона, при динамических проявлениях – через силу тока (в системе СИ за единицу заряда принят 1 Кулон (Кл) – электрический заряд, переносимый черезпоперечное сечение Sза 1 секунду при постоянной силе тока, равной 1 Амперу). Дискретность электрического заряда проявляется в том, что существует минимальный элементарный (неделимый) заряд. Элементарным положительным зарядом обладают протоны(qp=+e =+1, 6∙ 10-19 Кл), элементарным отрицательным зарядом обладают электроны (qe= -e= =-1, 6∙ 10-19 Кл). Атомы вещества в целом нейтральны, так как суммарный заряд всех протонов в ядре атома компенсируется суммарным зарядом электронов. При определенных условиях (при трении тел, при их облучении и др.)баланс положительно и отрицательно заряженных частицможет нарушаться и тогда макротело становится заряженным. Таким образом, зарядлюбого телаявляется целым кратным от элементарного заряда e: Идеализированные модели заряженных тел: 1) точечный заряд – заряженное тело формой и размерами которого можно пренебречь по сравнению с расстояниями, рассматриваемыми в задаче; 2)бесконечно длинная нить и бесконечная плоскость‒ заряженные тела, размеры которых много больше расстояний, рассматриваемых в задаче. Движущиеся заряженные частицы вещества могут вызывать ряд специфических эффектов (тепловых, магнитных, химических), которые не наблюдаются для статических зарядов. Поэтому движение заряженных частиц можно рассматривать как особое явление. Микроток – это движение отдельно взятой заряженной частицы. Например, в модели атома Резерфорда движение электрона вокруг ядра можно рассматривать как микроток. Макроток– упорядоченное движение совокупности заряженных частиц. Тепловое хаотическое движение элементарных частиц вещества не создает макротока, так как в силу равновероятности всех направлений движения соответствующие микротоки компенсируют друг друга. Ток проводимости– упорядоченное движение свободных заряженных частиц в среде или в вакууме (ток в металлах, в растворах электролитов, пучок электронов в вакуумной электронно-лучевой трубке и т.п.), вызванное действием электрического поля. Конвекционный ток– упорядоченное движение заряженных частиц, вызванное причинами, не связанными с электрическим полем. Многие специфические эффекты, вызванные движением заряженных частиц, зависят не от величины перенесенного заряда, а от скорости его переноса. Сила тока (I) – скалярная физическая величина, характеризующая скорость переноса заряда через рассматриваемую поверхность, численно равна абсолютной величине заряда, прошедшего через поперечное сечение проводника за единицу времени:
Сила тока измеряется в Амперах. Ампер относится к основным единицам СИ. Электромагнитное поле – особая материальная среда, передающаявзаимодействие между заряженными телами или частицами. Согласно модели Максвелла, электромагнитное поле распространяется в пространстве со скоростью 300000 км/св виде электромагнитной волны. Частными проявлениями электромагнитного поля являются электрическое и магнитное поля, обнаружение которых определяется условиями возникновения и выбранной для наблюдения системой отсчета. Электрическое поле ‒ одна из составляющих электромагнитного поля.Электрическое поле может быть создано двумя способами: ‒ неподвижными зарядами (электростатическое поле); ‒ переменным магнитным полем (вихревое электрическое поле). Электростатическое поле‒ это особый вид материи, передающий взаимодействие между неподвижными заряженными частицами или телами. Электростатическое поле создается неподвижными электрическими зарядами и обнаруживается по действию сил на помещенные в него заряженные тела.Таким образом, заряды по отношению к полю могут выполнять две функции: источника поля и индикатора поля. Магнитное поле – одна из составляющих электромагнитного поля. Это особый вид материи, передающий взаимодействие между движущимися зарядами или токами.Магнитное поле может быть создано двумя способами: ‒ движущимися зарядами (токами); ‒ переменным электрическим полем. Магнитное поле обнаруживается по действию сил на движущиеся частицы, токи или на магнитную стрелку.Таким образом, токи по отношению к магнитному полю могут выполнять две функции: источника поля и индикатора поля. Электростатическое поле Основные задачи, возникающие при изучении электростатического поля: ‒ введение количественных характеристик поля и анализ его свойств; ‒ расчет полей при известных зарядах, создающих поле; ‒ расчет действий поля на помещенные в него заряды и особенности движения заряженных частиц в электрических полях. Создающих поле Напряженность и потенциал поля в некоторой точкезависят от: ‒ величины зарядов, создающих поле; ‒ их конфигурации (формы заряженных тел); ‒ положения точки в поле; ‒ электрических свойств среды, в которой существует поле. В нижеприведенных формулах для расчета модуля напряженностизаряд|Q| берется по абсолютной величине, без учета знака заряда, а в формулах для расчета потенциала знак заряда, создающего поле, учитывается–( Модульнапряженностии потенциал поля, создаваемоготочечным зарядом:
где r – расстояние от заряда Q до точки, в которой определяются напряженность и потенциал. Модуль напряженности и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы: E=0;
Модуль напряженностии потенциал поля, создаваемогобесконечной прямой равномерно заряженной нитью или бесконечно длинным цилиндром с линейной плотностью заряда
где r – расстояние от нити или оси цилиндра до точки, в которой определяются характеристики поля. Модуль напряженности и потенциал поля, создаваемого бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда
где r – расстояние от плоскости до точки, в которой определяется потенциал поля. Принцип суперпозиции электрических полей Если в одной и той же точке пространства созданы два или несколько полей, то эти поля не взаимодействуюти не искажают друг друга, а их характеристики складываются, причем напряженности складываются векторно, а потенциалы – алгебраически:
В случае зарядов, непрерывно распределенных по длине тела, по его поверхности или объему, напряженность и потенциал поля, создаваемого этими зарядами, так же можно найти на основании принципа суперпозиции, поскольку любое заряженное тело можно рассматривать как систему бесконечно большого числа точечных зарядов. В этом случае принцип суперпозиции принимает вид:
Например, когда заряд равномерно распределен вдоль нити с линейной плотностью τ , то на нити выделяется малый участок длиной dl с зарядомdQ = τ dl. Такой заряд можно рассматривать как точечный и применять соответствующие формулы:
где Интегрирование по формулам (3.23) и (3.24) с учетом (3.25) ведется по всей длинеl заряженной нити(см. примеры 2 и 3, стр. 115- 120). Магнитное поле Основные задачи, возникающие при изучении магнитного поля: ‒ введение количественных характеристик поля и анализ его свойств; ‒ расчет полей при известных токах, создающих поле; ‒ расчет действий поля на помещенные в него токи и заряды, особенности движения заряженных частиц в магнитных полях. Теорема Остроградского – Гаусса (теорема о потоке вектора В) длямагнитного поля Поток вектора индукции магнитного поля через произвольную замкнутую поверхность равен нулю:
Эта теорема является математическим выражениемвихревого характера магнитного поля, то есть свойства замкнутостиего силовых линий. Закон Био-Савара-Лапласа Закон Био-Савара-Лапласа позволяет вычислять индукцию магнитного поля, созданного бесконечно малым элементом токаIdlна расстоянииrот этого элемента:
где α – угол между направлением элемента провода μ – магнитная проницаемость среды, в которой существует поле. L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA1yTc38MA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPzW7CMAzH75N4h8hIu410oCHoCAhNQkzjNOABrMY0 FY1TkkC7t58Pk3az5f/Hz6vN4Fv1oJiawAZeJwUo4irYhmsD59PuZQEqZWSLbWAy8EMJNuvR0wpL G3r+pscx10pCOJVowOXclVqnypHHNAkdsdwuIXrMssZa24i9hPtWT4tirj02LA0OO/pwVF2Pdy+9 fbzd35qDm11258P8K+6X++vMmOfxsH0HlWnI/+I/96cV/KngyzMygV7/AgAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEA1yTc38MAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" strokecolor="black [3213]" strokeweight="1pt">
 определяется правилом векторного произведения: вектор определяется правилом векторного произведения: вектор  перпендикулярен плоскости, в которой лежат векторы перпендикулярен плоскости, в которой лежат векторы 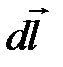 и и  , и направлен в ту сторону, откуда кратчайший поворот от , и направлен в ту сторону, откуда кратчайший поворот от 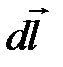 к к  кажется происходящим против часовой стрелки (см. Pис. 3.12). кажется происходящим против часовой стрелки (см. Pис. 3.12).
Коэффициент Магнитные свойства вещества По магнитным свойствам все вещества делятся на три группы: диамагнетики, парамагнетики, ферромагнетики. Каждый электрон, движущийся вокруг ядра атома можно рассматривать, как микроток, обладающий магнитным моментом Диамагнетики – вещества, атомы которых в отсутствие магнитного поля не обладают собственным магнитным моментом. Парамагнетики – вещества, атомы которых в отсутствие магнитного поляобладают собственным магнитным моментом, но, вследствие тепловогодвижения атомов, эти моменты ориентированы в пространстве хаотически так, что суммарный магнитный момент всего образца равен нулю. Ферромагнетики – вещества, у которых существуют макрообласти спонтанного намагничивания - домены с размерами порядка (1-10)мкм. В отсутствие внешнего поля магнитные моменты доменов ориентированы хаотически, поэтому образец в целом не намагничен. Внешнее магнитное поле меняет состояние не отдельных атомов, а доменов, именно с этим связаныособыесвойства ферромагнетиков (см. ниже). Заряды Объединяя ранее рассмотренные силы, действующие на заряженную частицу со стороны электрического имагнитного поля, получим уравнение для обобщенной силы Лоренца:
Материальныеуравнения Материальные уравнения – этоуравнения, отражающие реакцию вещества на поле. Они связываютхарактеристики вещества, характеристики поля и характеристики явлений, возникающих в веществе под действием поля. Будем записывать этиуравнениядля ситуации, когда среда, в которой существует поле однородная, изотропная и линейная. Последнее свойство означает, что изменения, происходящие в веществе, пропорциональны соответствующей характеристике поля. ‒ Для металловплотность тока пропорциональна напряженности электрического поля:
‒ Для диэлектриков вектор поляризации (поляризованность) пропорционален напряженности электрического поля:
‒ Для магнетиков вектор намагничивания (намагниченность) пропорционалениндукции магнитного поля:
Уравнения (3.84) и (3.85) иногда преобразуют к виду:
где ε – диэлектрическая проницаемость вещества (для линейных сред – постоянная величина, не зависящая от напряженности поля); μ – магнитная проницаемость вещества (для линейных сред – постоянная величина, не зависящая от индукцииполя);
D – индукция электрического поля (вектор электрического смещения) – дополнительная характеристика электрического поля, описывающая внешнее поле, создаваемое свободными зарядами с учетом их перераспределения в пространстве, вызванного появлением индуцированных связанных зарядов в диэлектрике; Н – напряженность магнитного поля– дополнительная характеристика магнитного поля, описывающая внешнее поле, создаваемое свободными токами. Пример 1. Два точечных электрических заряда Решение. В данной задаче рассматривается ситуация, когда заряды
Вектор Модуль вектора
где
Подставляя выражение
В соответствии с принципом суперпозиции электрических полей, потенциал φ результирующего поля, создаваемого двумя зарядами
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
В нашем случае согласно формулам (5) и (6) получим
или
Сила, действующая на точечный зарядQ, находящийся в электрическом поле в точке А
где напряженность находится из выражения (4). Произведем вычисления:
Ответ: Пример 2. Определить напряженность электрического поля, созданного бесконечной равномерно заряженной (с линейной плотностью заряда Решение. В данной задаче электрическое поле создается бесконечно заряженной нитью, заряд которой линейно распределен. Разобьем нить на элементы длиной По принципу суперпозиции напряженность
Направления
Модуль вектора напряжённости равен:
Замечаем, что под интегралом три переменных l, r и a, находим
 (2) (2)
Чтобы связать переменные dl и Рассмотрим сначала вспомогательный отрезок
используя (2)
Подставляем (2) и (3) в (1), получим
При интегрировании по всей длине нити угол a будет меняться в пределах от -p/2 до +p/2(так как aотсчитывается от оси х, а нить бесконечная и ее концы расположены симметрично относительно точки A).
Аналогично можно найти
Проверим выражение (5) по размерности:
Ответ: Пример 3. На тонком стержне длиной l = 10см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 5 см от ближайшего конца находится точечный заряд Q1=40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне. Найти потенциал φ в точке А, расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l. Решение.(1 часть) Для определения линейной плотности заряда стержня предположим, что заряженный стержень создает поле, а заряд
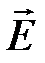 напряженность поля, созданного стержнем в точке, где расположен заряд напряженность поля, созданного стержнем в точке, где расположен заряд  . Для определения напряженности выделим на стержне элемент длиной dr с зарядом dQ = τ dr (рис. 3.19). Этот заряд можно рассматривать как точечный, тогда численное значение напряженности в этой точке определим по формуле для точечного заряда: . Для определения напряженности выделим на стержне элемент длиной dr с зарядом dQ = τ dr (рис. 3.19). Этот заряд можно рассматривать как точечный, тогда численное значение напряженности в этой точке определим по формуле для точечного заряда:
По принципу суперпозиции напряженность
Направления
Согласно (1), сила взаимодействия равна
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
Найденная единица является единицей линейной плотности заряда.Произведем вычисления:
(2 часть) Электрическое поле в точке А создают точечный заряд
где Потенциал dφ , создаваемыйточечным зарядом
Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке
Выполним интегрирование:
Подставим (5) в (4)
Подставим числовые значения физических величин вСИ (1/(4π ε 0)=9.109 м/Ф,
Ответ:
 в точке А, находящейся на расстоянии а. в точке А, находящейся на расстоянии а.
Решение. В данной задаче плоскость является источником электрического поля, конфигурация силовых линий которого изображена на рис. 3.20. Для определения напряженности Евоспользуемся теоремой Остроградского-Гаусса для электростатики
Проведем вспомогательную гауссову поверхность S.Из соображений симметрии, вспомогательную поверхность выбираем так, чтобы она содержала две плоскости, параллельные заряженной, например, цилиндр, ось которого располагается параллельно силовым линиям, а основания симметрично относительно заряженной плоскости и одно из них проходит через точку А. Определим поток через выбранную поверхность:
где Заряд сосредоточен на участке плоскости, который вырезается цилиндром (заштрихованный участок плоскости) равен
Подставляя (2) и (3) в (1), получим:
откуда
Проверим полученное выражение по размерности:
Ответ:
 10 см заряжен равномерно с объемной плотностью зарядов 10 см заряжен равномерно с объемной плотностью зарядов  =15нКл/м3. Определить напряженность поля в точках 1 и 2, лежащих на расстояниях =15нКл/м3. Определить напряженность поля в точках 1 и 2, лежащих на расстояниях  , ,  от центра шара (см. Рис. 3.21). от центра шара (см. Рис. 3.21).
Популярное: |
Последнее изменение этой страницы: 2016-07-12; Просмотров: 1082; Нарушение авторского права страницы