
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Система уравнений Максвелла для электромагнитного поля в вакууме ⇐ ПредыдущаяСтр 6 из 6
Окончание табл. 3.3
В веществе под действием поля происходят изменения в расположении и характере движении микрочастиц, в результате чего возникают разнообразные явления: электризация, поляризация, намагничивание, электрический ток. Вещество, в свою очередь, влияет на характеристики поля. Таким образом, для полного описания электромагнитных взаимодействий помимо записанных уравнений Максвелла необходимы ещё две группы уравнений. Уравнения, определяющие действие поля на находящиеся в нем Заряды Объединяя ранее рассмотренные силы, действующие на заряженную частицу со стороны электрического имагнитного поля, получим уравнение для обобщенной силы Лоренца:
Материальныеуравнения Материальные уравнения – этоуравнения, отражающие реакцию вещества на поле. Они связываютхарактеристики вещества, характеристики поля и характеристики явлений, возникающих в веществе под действием поля. Будем записывать этиуравнениядля ситуации, когда среда, в которой существует поле однородная, изотропная и линейная. Последнее свойство означает, что изменения, происходящие в веществе, пропорциональны соответствующей характеристике поля. ‒ Для металловплотность тока пропорциональна напряженности электрического поля:
‒ Для диэлектриков вектор поляризации (поляризованность) пропорционален напряженности электрического поля:
‒ Для магнетиков вектор намагничивания (намагниченность) пропорционалениндукции магнитного поля:
Уравнения (3.84) и (3.85) иногда преобразуют к виду:
где ε – диэлектрическая проницаемость вещества (для линейных сред – постоянная величина, не зависящая от напряженности поля); μ – магнитная проницаемость вещества (для линейных сред – постоянная величина, не зависящая от индукцииполя);
D – индукция электрического поля (вектор электрического смещения) – дополнительная характеристика электрического поля, описывающая внешнее поле, создаваемое свободными зарядами с учетом их перераспределения в пространстве, вызванного появлением индуцированных связанных зарядов в диэлектрике; Н – напряженность магнитного поля– дополнительная характеристика магнитного поля, описывающая внешнее поле, создаваемое свободными токами. Пример 1. Два точечных электрических заряда Решение. В данной задаче рассматривается ситуация, когда заряды
Вектор Модуль вектора
где
Подставляя выражение
В соответствии с принципом суперпозиции электрических полей, потенциал φ результирующего поля, создаваемого двумя зарядами
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
В нашем случае согласно формулам (5) и (6) получим
или
Сила, действующая на точечный зарядQ, находящийся в электрическом поле в точке А
где напряженность находится из выражения (4). Произведем вычисления:
Ответ: Пример 2. Определить напряженность электрического поля, созданного бесконечной равномерно заряженной (с линейной плотностью заряда Решение. В данной задаче электрическое поле создается бесконечно заряженной нитью, заряд которой линейно распределен. Разобьем нить на элементы длиной По принципу суперпозиции напряженность
Направления
Модуль вектора напряжённости равен:
Замечаем, что под интегралом три переменных l, r и a, находим
 (2) (2)
Чтобы связать переменные dl и Рассмотрим сначала вспомогательный отрезок
используя (2)
Подставляем (2) и (3) в (1), получим
При интегрировании по всей длине нити угол a будет меняться в пределах от -p/2 до +p/2(так как aотсчитывается от оси х, а нить бесконечная и ее концы расположены симметрично относительно точки A).
Аналогично можно найти
Проверим выражение (5) по размерности:
Ответ: Пример 3. На тонком стержне длиной l = 10см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 5 см от ближайшего конца находится точечный заряд Q1=40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность τ заряда на стержне. Найти потенциал φ в точке А, расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l. Решение.(1 часть) Для определения линейной плотности заряда стержня предположим, что заряженный стержень создает поле, а заряд
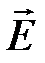 напряженность поля, созданного стержнем в точке, где расположен заряд напряженность поля, созданного стержнем в точке, где расположен заряд  . Для определения напряженности выделим на стержне элемент длиной dr с зарядом dQ = τ dr (рис. 3.19). Этот заряд можно рассматривать как точечный, тогда численное значение напряженности в этой точке определим по формуле для точечного заряда: . Для определения напряженности выделим на стержне элемент длиной dr с зарядом dQ = τ dr (рис. 3.19). Этот заряд можно рассматривать как точечный, тогда численное значение напряженности в этой точке определим по формуле для точечного заряда:
По принципу суперпозиции напряженность
Направления
Согласно (1), сила взаимодействия равна
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы:
Найденная единица является единицей линейной плотности заряда.Произведем вычисления:
(2 часть) Электрическое поле в точке А создают точечный заряд
где Потенциал dφ , создаваемыйточечным зарядом
Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке
Выполним интегрирование:
Подставим (5) в (4)
Подставим числовые значения физических величин вСИ (1/(4π ε 0)=9.109 м/Ф,
Ответ:
 в точке А, находящейся на расстоянии а. в точке А, находящейся на расстоянии а.
Решение. В данной задаче плоскость является источником электрического поля, конфигурация силовых линий которого изображена на рис. 3.20. Для определения напряженности Евоспользуемся теоремой Остроградского-Гаусса для электростатики
Проведем вспомогательную гауссову поверхность S.Из соображений симметрии, вспомогательную поверхность выбираем так, чтобы она содержала две плоскости, параллельные заряженной, например, цилиндр, ось которого располагается параллельно силовым линиям, а основания симметрично относительно заряженной плоскости и одно из них проходит через точку А. Определим поток через выбранную поверхность:
где Заряд сосредоточен на участке плоскости, который вырезается цилиндром (заштрихованный участок плоскости) равен
Подставляя (2) и (3) в (1), получим:
откуда
Проверим полученное выражение по размерности:
Ответ:
 10 см заряжен равномерно с объемной плотностью зарядов 10 см заряжен равномерно с объемной плотностью зарядов  =15нКл/м3. Определить напряженность поля в точках 1 и 2, лежащих на расстояниях =15нКл/м3. Определить напряженность поля в точках 1 и 2, лежащих на расстояниях  , ,  от центра шара (см. Рис. 3.21). от центра шара (см. Рис. 3.21).
Решение. В данной задаче электрическое поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает сферической симметрией: силовые линии ‒ прямые выходящие из центра шара (заряд шара считается положительным).Вспомогательные гауссовы поверхности выбираем сферической формы. Характер функциональной зависимости Определим поток через выбранную сферическую поверхность
где Заряд, попадающий внутрь выделенной поверхности а) внутри шара при
б) вне шарапри
Воспользуемся теоремой Остроградского-Гаусса для электростатики
Подставляя (1) и (2) в (3), получим:
Откуда напряженность внутри шара
напряженность вне шара
Проверим выражение (4) и (5) по размерности
Произведем вычисления:
Ответ: Пример 6. Электрическое поле создается двумя зарядами
 и и 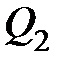 , а заряд , а заряд 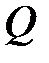 есть пробный заряд, помещенный в это поле. Для определения работы есть пробный заряд, помещенный в это поле. Для определения работы  сил поля воспользуемся соотношением сил поля воспользуемся соотношением
где
Тогда
или
Проверим, дает ли правая часть равенства единицу работы (Дж):
Подставим числовые значения физических величин в СИ: Q=50 .10-9Кл, Q1=4.10-6Кл, Q2= 2.10-6Кл, a= 0, 1 м,
Ответ: Пример 7. В пространство между пластинами плоского конденсатора влетает электрон со скоростью Решение. В задаче рассматривается сложное криволинейное движение электрона в электрическом поле конденсатора. На основании принципа независимости движений его можно представить состоящим из двух движений – по горизонтали (по оси х) и по вертикали (по оси у). Характер поступательного движения определяется на основе II закона Ньютона, а конкретные параметры движения на основе кинематических законов.
 На электрон действует единственная сила со стороны электрического поля: На электрон действует единственная сила со стороны электрического поля:  Поскольку напряженность поля направлена вверх, а заряд электрона отрицательный, Поскольку напряженность поля направлена вверх, а заряд электрона отрицательный,  направлена вниз и по модулю равна: направлена вниз и по модулю равна:
В проекциях на координатные оси:
По рисунку видно, что Запишем кинематические законы для этих видов движения:
Модуль скорости определяется выражением:
а направление
Откуда
Учитывая, что для однородного электрического поля
Проверим полученные выражения по единицам измерения
Проведем вычисления:
Ответ: Пример 8. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью Решение. В данной задаче рассматривается движущийся поступательно в электрическом поле электрон. На него действует электрическая сила, под действием которой он движется равноускорено против направления поля. При этом электрическая сила будет совершать работу по перемещению электрона против поля, равную изменению кинетической энергии электрона:
где m – масса электрона; Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда е на разность потенциалов U: A=eU.(2) Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона. Приравняв правые части равенств (1) и (2), получим:
где Отсюда искомая разность потенциалов Проверим выражение это по размерности:
Произведем вычисления:
Ответ: U=204, 7 B. Пример 9. Пластины плоского конденсатора изолированы друг от друга слоем диэлектрика. Конденсатор заряжен до разности потенциалов 1 кВ и отключен от источника напряжения. Определите диэлектрическую проницаемость диэлектрика, если при его удалении разность потенциалов между пластинами конденсатора возрастает до3 кВ. Решение. В данной задаче рассматривается влияние диэлектрика на емкость конденсатора.Поскольку конденсатор отключен от источника напряжения, то его заряд в обоих случаях будет одинаковым:
Тогда Произведем вычисления: Ответ: Пример 10. Конденсатор емкостью Решение. В данной задаче рассматриваются конденсаторы, устройства для накопления электрического заряда. Энергия заряженного конденсатора определяется по формуле
где С – емкость конденсатора или батареи конденсаторов. Энергия, израсходованная на образование искры:
где Выразив в формуле (2) энергии
где Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов
Подставив выражение
или
Проверим полученное выражение по размерности:
Произведем вычисления:
Ответ: Пример 11.Определите ЭДСи внутреннее сопротивление Решение. В данной задаче рассмотрена замкнутая цепь постоянного тока. Силы токаI1и I2 определим по закону Ома для замкнутой цепи
Популярное:
|
Последнее изменение этой страницы: 2016-07-12; Просмотров: 946; Нарушение авторского права страницы