Элективные и факультативные курсы

Содержание

Введение…………………………………………………………………………
Глава I Профильная школа в условиях модернизации образования………. 1.1 Основные понятие профильного обучения информатике……………….
1.2 Элективные и факультативные курсы…………………………………….
1.3 Особенности элективных курсов по информатике ……………………… 1.4 Вывод по первой главе………………………………………………………
Глава II Методика преподавания темы «Решение прикладных задач» в курсе информатики в классах социально-экономического профиля………
2.1Математические методы для решения экономических задач…………… 2.1.1 Линейное программирование…………………………………….. 2.1.2 Транспортная задача………………………………………………. 2.1.3 Теория игр…………………………………………………………..
2.2.Экономико-математические методы в различных УМК по информатике
2.3 Элективный курс «Решение прикладных задач» в классах социально-экономического профиля………………………………………………………. 2.4. Методика преподавания элективного курса «Решение прикладных задач» в классах социально-экономического профиля………………………. 2.4.1Методические рекомедации по изучению темы «Решение прикладных задач»………………………………………………………. 2.4.2 Поурочное планирование………………………………………….. 2.4.3 Апробация элективного курса «Решение прикладных задач»….. 2.5 Вывод по II главе…………………………………………………………….
Заключение....................................................................................................
Литература.....................................................................................................
Приложения................................................................................................

Введение

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания. Термин " модель" широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений.

Модель - объект или описание объекта, системы для замещения (при определенных условиях предложениях, гипотезах) одной системы (т.е. оригинала) другой системы для изучения оригинала или воспроизведения его каких - либо свойств. Модель - результат отображения одной структуры на другую.

Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез. Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.

Возможности моделирования, то есть перенос результатов, полученных в ходе построения и исследования модели, на оригинал основаны на том, что модель в определенном смысле отображает (воспроизводит, моделирует, описывает, имитирует) некоторые интересующие исследователя черты объекта. Моделирование как форма отражения действительности широко распространено, и достаточно полная классификация возможных видов моделирования крайне затруднительна, хотя бы в силу многозначности понятия " модель", широко используемого не только в науке и технике, но и в искусстве, и в повседневной жизни.

Применительно к естественным и техническим наукам принято различать следующие виды моделирования:

1. концептуальное моделирование, при котором совокупность уже известных фактов или представлений относительно исследуемого объекта или системы истолковывается с помощью некоторых специальных знаков, символов, операций над ними или с помощью естественного или искусственного языков;

2. физическое моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы, причем между процессами в объекте-оригинале и в модели выполняются некоторые соотношения подобия, вытекающие из схожести физических явлений;

3. структурно-функциональное моделирование, при котором моделями являются схемы (блок-схемы), графики, чертежи, диаграммы, таблицы, рисунки, дополненные специальными правилами их объединения и преобразования;

4. математическое (логико-математическое) моделирование, при котором моделирование, включая построение модели, осуществляется средствами математики и логики;

5. имитационное (программное) моделирование, при котором логико-математическая модель исследуемого объекта представляет собой алгоритм функционирования объекта, реализованный в виде программного комплекса для компьютера.

Разумеется, перечисленные выше виды моделирования не являются взаимоисключающими и могут применяться при исследовании сложных объектов либо одновременно, либо в некоторой комбинации. Кроме того, в некотором смысле концептуальное и, скажем, структурно-функциональное моделирование неразличимы между собой, так как те же блок-схемы, конечно же, являются специальными знаками с установленными операциями над ними.

Изучение " Решение прикладных задач" в классах социально-экономического профиля поможет сформировать у учащихся умение анализировать условие задачи, продумывать последовательность действий, направленных на ее выполнение. Контролировать правильность своих действий на всех этапах работы и корректировать их в случаях допущенной ошибки, то есть направить учащихся на формирование широкого спектра умений, которые будут необходимы в дальнейшей учебной и учебно-трудовой деятельности ученика, а в будущем и любой профессиональной деятельности.

Цель: изучение теоретических положений по исследованию операций и создание элективного курса " Решение прикладных задач" в классах социально-экономического профиля.

Объект исследования: методы исследования по информатике.

Предмет исследования: экономико-математические методы в классах социально-экономического профиля.

Задачи исследования:

1. Изучить теоретический материал

2. Выбрать задачи из различных учебных и методических пособий для практической реализации

3. Применять алгоритмы для решения задач

4. Разработать элективный курс «Решение прикладных задач» для классов социально-экономического профиля

5. Методика преподавания элективного курса в классах социально-экономического профиля

Гипотеза: создать методику преподавания элективного курса, а также улучшить логическое мышление и повысит уровень подготовки по информатике.

Новизна работы заключается в создании своего элективного курса для классов социально-экономического профиля.

Теоретическое значение – данная работа поможет в обучении экономико-математических задач и моделированию учащихся старших классов в рамках элективного курса по информатике.

Практическая значимость состоит в том, что конкретный теоретический и практический материал может быть использован для лекций по методике преподавания информатики и математики.

Глава 1. Профильная школа в условиях модернизации образования

1.1 Понятие электив профильного образования

В последние годы резко повысилась роль образования в жизни каждого человека. Учение на протяжении всей жизни как единственно возможный в современных условиях способ жизнедеятельности человека – необходимая предпосылка и условие для эффективной деятельности во всех сферах общественного и личного бытия, а также поступательного развития человеческого общества. Для выполнения данных задач требуется образование иного качества, чем раньше.

В условиях постоянного возрастания объема информации человеку нужно уметь ориентироваться в ней, уметь ставить перед собой цель, достигать ее, уметь адекватно оценивать себя и прогнозировать развитие дальнейших событий. Но в массовой школе преобладает традиционная модель обучения, ориентированная на усвоение знаний, умений и навыков в каждой области знаний. В результате этого в образовании появляются различные противоречия. Также у многих учащихся школ не сформирована потребность в своём дальнейшем саморазвитии и получении образования после окончания школы, нет также устойчивой мотивации на приложение усилий для получения качественного профессионального образования, слишком рано, уже в школьный период, наступает замедление процессов развития учащихся как личности. Это и есть неудовлетворительные результаты, которые должна устранить профильная школа.

В наше время активно модернизируется вся система образования. Данная модернизация направлена на значительное обновление содержания и процесса обучения, а именно:

1. введение системно-деятельностного и личностно-ориентированного подходов к обучению и воспитанию;

2. формирование самостоятельной учебно-познавательной активности учащихся.

Таким образом, после модернизации школа должна будет предоставить учащимся возможность самообучения, саморазвития и самосовершенствования в различных направлениях.

Одним из направлений для модернизации является переход к профильной школе. Профильное обучение предоставляет новые возможности в организации учебно-воспитательного процесса в школе. Профильная школа может способствовать осознанному профессиональному самоопределению и необходимой социальной зрелости ученика.

Согласно реформе образования в двух последних классах каждому гражданину России должна быть предоставлена возможность выбора одной из 5-6 программ: гуманитарной, естественнонаучной, математики и информатики, экономики и права, технической, эколого-аграрной. Каждый школьник должен иметь возможность получить профильное образование за счет государства. Профильная школа позволит преодолеть не только формальный универсализм старшей школы, но и объективный разрыв между требованиями вуза и возможностями системы общего образования. Такую школу предполагалось сделать к 2004-2005 годам. На данный момент во многих школах сделаны профильные классы, однако вопросы перехода к профильному образованию не достаточно проработаны.

Исследования показали, что в школах по-разному понимают особенности профильного обучения, как правило, затруднения связаны с преодолением его содержания, комплектования методического сопровождения. Также, согласно исследованиям, профильное обучение дает положительные результаты.

В соответствии с одобренной Минобразованием России «Концепцией профильного обучения на старшей ступени общего образования» дифференциация содержания обучения в старших классах осуществляется на основе различных сочетаний курсов трех типов: базовых, профильных, элективных. Каждый из курсов этих трех типов вносит свой вклад в решение задач профильного обучения. Однако можно выделить круг задач, приоритетных для курсов каждого типа.

Базовые общеобразовательные курсы отражают обязательную для всех школьников инвариативную часть образования и направлены на завершение общеобразовательной подготовки обучающихся.

Профильные курсы обеспечивают углубленное изучение отдельных предметов и ориентированы, в первую очередь, на подготовку выпускников школы к последующему профессиональному образованию.

Элективные же курсы связаны, прежде всего, с удовлетворением индивидуальных образовательных интересов, потребностей и склонностей каждого школьника. Именно они по существу и являются важнейшим средством построения индивидуальных образовательных программ, так как в наибольшей степени связаны с выбором каждым школьником содержания образования в зависимости от его интересов, способностей, последующих жизненных планов. Элективные курсы как бы «компенсируют» во многом достаточно ограниченные возможности базовых и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников.

Ранее было сказано, что профильное обучение направлено на реализацию личностно-ориентированного учебного процесса, таким образом, переход к профильному обучению преследует следующие цели:

1. обеспечить углублённое изучение отдельных дисциплин программы полного общего образования;

2. создать условия для значительной дифференциации содержания обучения старшеклассников, с широкими и гибкими возможностями построения школьниками индивидуальных образовательных программ;

3. способствовать установлению равного доступа к полноценному образованию разным категориям учащихся в соответствии с их индивидуальными склонностями и потребностями;

4. расширить возможности социализации учащихся, обеспечить преемственность между общим и профессиональным образованием, в том числе более эффективно подготовить выпускников школы к освоению программ высшего профессионального образования.

Вывод по первой главе.

В этой главе рассмотрены особенности элективных курсов, а также основные понятия профильного обучения. Элективные курсы, хотя и различаются по целям и содержанию, должны соответствовать запросам учащихся, которые их выбирают. Элективные курсы как бы «компенсируют» во многом достаточно ограниченные возможности базовых и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников.

Глава II Методика преподавания темы «Решение прикладных задач» в курсе информатики в классах социально-экономического профиля.

2.1 Математические методы для решения экономических задач

Экономико-математические методы необходимы в повседневной жизни для принятия правильного решения, дать надежный обоснованный вариант решения экономической задачи. Решение большинства задач экономической практики базируется на элементарной математике: арифметике, алгебре, геометрии, комбинаторике, логике. Это задачи с дробями, процентами, пропорциями, прогрессиями, уравнениями, а также на построение функций и графиков.

Наряду с элементарной математикой и логикой рассматриваются также задачи, требующие применения аппарата высшей математики, особенно в теории вероятностей и математической статистике, а также в таких сравнительно молодых методах, как математическое программирование (линейное, нелинейное, динамическое), теория игр и статистических решений, теория массового обслуживания (теория очередей), метод статистических испытаний (Монте-Карло), сетевое планирование.

Каждый из экономико-математических методов, имеет свою область применения.

Элементарная арифметика и алгебра (уравнения, функции и графики) применяются для экономических расчетов, связанных с определением долей, процентов материальных ресурсов, составлением пропорций, счетом денег, вычислением прибыли, налогов, рентабельности и т.п.

Арифметические и геометрические прогрессии позволяют вести расчеты, связанные с последовательностями экономических показателей и объектов (например, так называемые " пирамиды" ).

Комбинаторика дает возможность определять результаты, возникающие при различных сочетаниях экономических объектов, их перестановках и размещениях.

Геометрия предназначена для вычислений, связанных с пространственными отношениями и формами объектов, интересующих экономиста.

Логика позволяет оценить экономическую ситуацию с точки зрения истинности или ложности используемой информации, разобраться в запутанных обстоятельствах, найти рациональный выход из затруднительного положения.

Линейное программирование предназначено для выработки оптимального решения экономической задачи для случая, когда, ее условия и имеющиеся ограничения описываются уравнениями или неравенствами 1-й степени.

Нелинейное программирование служит для выработки оптимального решения экономической задачи в том случае, когда ее условия и ограничения описываются уравнениями или неравенствами 2-й и более степени.

Динамическое программирование дает возможность выбора оптимального плана многоэтапных действий, в которых результат каждого последующего этапа зависит от предыдущего.

Теория вероятностей обосновывает экономические расчеты, связанные с явлениями случайного характера. Математическая статистика обеспечивает сбор, обработку и анализ экономических статистических материалов.

Теория массового обслуживания (теория очередей) дает расчеты производственно-экономических показателей и выработку необходимых рекомендаций для массовых повторяющихся процессов обслуживания. Метод статистических испытаний (Монте-Карло) служит для производства экономических расчетов, связанных с явлениями случайного характера, на основе искусственно произведенных статистических материалов.

Теория игр служит для выработки экономических решений в условиях неопределенности, неясности ситуации, вызванной сознательными, злонамеренными действиями конфликтующей стороны. Теория статистических решений применяется для выработки экономических решений в условиях неопределенности, вызванной объективными обстоятельствами, которые либо неизвестны, либо носят случайный характер.

Сетевое планирование применяется для составления и реализации рациональных планов ведения экономических операций, предусматривающих решение задачи в кратчайший срок и с наилучшими результатами.

В своей дипломной работе рассматриваются методы которые широко и наиболее часто используются в экономике, а также соответствует требованиям знаний, умений и навыков для учащихся социально-экономического профиля. На школьном этапе изучения математики, информатики и ИКТ наиболее эффективным будет изучение таких методов как арифметика, арифметические и геометрические прогрессии, комбинаторика, линейное программирование, теория вероятности и теория игр.

Одной из научных дисциплин по решению прикладных задач в экономике является исследование операций.

Линейное программирование.

Исследование операций в экономике – это научная дисциплина, целью которой является количественное обоснование принимаемых решений.

С помощью специальных математических методов решается определенный класс экономических задач. К таким задачам относятся:

1. задача об оптимальном использовании ограниченных ресурсов (сырьевых, трудовых, временных);

2. задача сетевого планирования и управления;

3. задачи массового обслуживания;

4. задачи составления расписания (календарного планирования);

5. задачи выбора маршрута и другие.

Оптимизационная задача, в которой целевая функция и неравенства (уравнения), входящие в систему ограничений являются линейными функциями, называется задачей линейного программирования.

Общая задача линейного программирования имеет вид:

(1.1) (1.2)

(1.3)

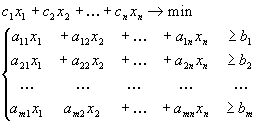
Функция (1.1) называется целевой функцией. Система (1.2) называется системой ограничений, а условие (1.3) – условием неотрицательности.

Геометрическая интерпретация ЗЛП. Графический метод решения ЗЛП

Графический метод решения ЗЛП основан на следующих утверждениях.

Система ограничений ЗЛП геометрически представляет собой выпуклый многоугольник или выпуклую многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы.

Целевая функция Z = c₁x₁ + c₂x₂ геометрически изображает семейство параллельных прямых, перпендикулярных вектору нормали N(с₁, с₂). Эти прямые называются линиями уровня.

Линия уровня – это прямая, вдоль которой целевая функция принимает фиксированное значение.

Теорема. При перемещении линии уровня в направлении вектора нормали N значение целевой функции возрастает, в противоположном направлении - убывает.

Графического метода решения ЗЛП.

1. В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;

2. Найти полуплоскость решения каждого неравенства системы (обозначить стрелками). Для определения полуплоскости необходимо выбрать любую контрольную точку, не лежащую на данной прямой. Подставить ее координаты в систему ограничений. Если неравенство выполняется, то нужно выбрать полуплоскость, содержащую контрольную точку. Если неравенство не выполняется нужно выбрать полуплоскость, не содержащую контрольную точку. В качестве контрольной точки рекомендуется выбирать точку с координатами (0; 0);

3. Найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;

4. Построить вектор нормали N. Начало вектора нормали в точке с координатами (0; 0), конец вектора в точке с координатами (с₁, с₂);

5. Через начало координат построить линию уровня, перпендикулярно к вектору нормали;

6. Перемещать линию уровня параллельно самой себе по области решения в угловые точки, достигая max f при движении вектора N (min f при движении в противоположном направлении);

7. Найти координаты точки max (min). Для этого необходимо решить систему уравнений прямых, которые пересекаются в этой точке или определить координаты по графику;

8. Вычислить значение целевой функции в этой точке (ответ).

Симплексный метод решения ЗЛП

Симплексный метод представляет собой схему получения оптимального плана за конечное число шагов.

Для использования симплексного метода ЗЛП должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.

Оптимизационные исследования ЗЛП удобно проводить, пользуясь симплекс-таблицами. Существует достаточно большое количество форм симплекс-таблиц. Воспользуемся одной из форм, по которой рекомендуется следующий порядок решения ЗЛП:

1. Математическая модель задачи приводится к канонической форме с помощью дополнительных неотрицательных переменных.

2. Определяется начальное базисное допустимое решение. Для этого переменные разбивают на две группы – основные (базисные) и неосновные. В качестве основных переменных следует выбрать (если возможно) переменные, каждая из которых входит только в одно из уравнений системы ограничений. Дополнительные переменные удовлетворяют этому правилу.

3. Составляется исходная симплекс-таблица (таблица 1), в которую записывают параметры, соответствующие начальному базисному допустимому решению:

3.1. Весовые коэффициенты c_j при переменных x_j(j = 1,..., n) целевой функции (строка C).

3.2. Весовые коэффициенты c_i при базисных переменных x_i(i = 1,..., m) целевой функции (столбец C_b).

3.3. Переменные x_i(i = 1, ..., m), которые входят в текущий базис (столбец A_b ).

3.4. Свободные коэффициенты b_i(i =1, ..., m) уравнений ограничений (столбец B). В этом же столбце находим оптимальный план задачи.

3.5. Элементы a_ij (i = 1, ..., m; j = 1, ..., n) матрицы условий задачи (столбцы A₁, ..., A_n ).

Таблица 1

А_б	С_б	В	c₁	...	c_j	...	c_k	...	c_n
A₁	...	A_j	...	A_k	...	A_n
А₁	c₁	b₁	a₁₁	...	a_1j	...	a_1k	...	a_1n
…	...	...	...	...	...	...	...	...	...
А_i	c_i	b_i	a_i1	...	a_ij	...	a_ik	...	a_in
…	...	...	...	...	...	...	...	...	...
A_r	c_r	b_r	a_r1	...	a_rj	...	a_rk	...	a_rn
…	...	...	...	...	...	...	...	...	...
A_m	c_m	b_m	a_m1	...	a_mj	...	a_mk	...	a_mn
m+1		S	S₁	...	S_j	...	S_k	...	S_n

3.6. Оценки S_j(j=1, ..., n) векторов условий A_j, которые определяются по формуле:

где c_i - весовые коэффициенты при базисных переменных.

Из этой формулы следует, что коэффициенты z_j вычисляются для каждого столбца как сумма почленных произведений коэффициентов c_iна одноименные коэффициенты j-го столбца. При заполнении симплекс-таблицы при условии, что рассматривается задача максимизации целевой функции, необходимо иметь в виду:

1. если S_j ³ 0 для всех j = 1, ..., n, то полученное решение является оптимальным;

2. если имеются S_j< 0и в столбцах A_j, соответствующих этим отрицательным оценкам, существует хотя бы один элемент a_ij> 0, то возможен переход к новому решению, связанному с большим значением целевой функции;

3. Из отрицательных оценок выбирают ту, у которой значение по абсолютной величине больше. Если имеется несколько одинаковых отрицательных оценок, то выбирают ту, которой соответствует максимальный коэффициент целевой функции c_i.

4. если имеются S_k< 0 и в столбце A_k все элементы a_ik£ 0, то в области допустимых решений целевая функция не ограничена сверху.

4. Определяется вектор A_k, который необходимо ввести в базис для улучшения решения, по наибольшему значению S_k. Переменная этого столбца x_k будет новой базисной переменной, которая вводится в базис. Столбец, содержащий эту переменную, называетсянаправляющим столбцом.

5. Определяется вектор, который нужно вывести из базиса, используя равенство:

Это условие позволяет найти направляющую строку. Переменная x_r, соответствующая этой строке, выводится из базисного решения и заменяется переменной x_k направляющего столбца. Элемент a_rk, который стоит на пересечении направляющего столбца и направляющей строки, называется разрешающим элементом.

6. Заполняется таблица соответствующая новому базисному решению. В этой таблице, прежде всего заполняются клетки строки r с вводимой переменной x_k. Для этого все элементы этой строки делятся на направляющий элемент. Получаются элементы новой строки:

b_r/a_rk, a_r₁/a_rk, ..., a_rn/a_rk.

Остальные элементы новой таблицы определяются по правилу прямоугольника:

Процесс вычислений заканчивается, когда найдено оптимальное решение.

Критерий оптимальности решения для нахождения максимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.

Критерий оптимальности решения для нахождения минимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

Метод искусственного базиса.

Если ограничения исходной задачи содержат единичную матрицу порядка М, то при неотрицательности правых частей уравнений определен первоначальный план, из которого с помощью симплекс – таблиц находится оптимальный план.

Если ограничения можно привести к виду:

Ах≤ А₀ при А₀≥ 0, то система ограничений содержит единичную матрицу всегда.

Если задача не содержит единичной матрицы и не приводится к указанному виду, то для решения задачи используется метод искусственного базиса.

Для получения единичной матрицы к каждому ограничению прибавляют по одной неотрицательной переменной, которые называются искусственными. Единичные вектора, соответствующие искусственным переменным, образуют искусственный базис.

В целевую функцию искусственные переменные добавляются с коэффициентом М, если задана задача на нахождение минимума. В этом случае величина М предполагается достаточно большим положительным числом. Если необходимо найти минимальное значение целевой функции, то искусственные переменные записывают с коэффициентом (-М), который предполагается достаточно малым отрицательным числом. Для нахождения оптимального плана в случае, если заранее не задана величина М, применяется симплекс-метод, который в таблице имеет на одну строку больше, чем обычная симплекс-таблица.

Строка оценок разбивается на две:

(m+1) – оценка, не зависящая от М;

(m+2) – коэффициент при М.

По (m+2) строке определяют вектор, подлежащий включению в базис. Итерационный процесс проводят до исключения из базиса всех искусственных векторов. Затем процесс продолжают по (m+1) строке обычным симплекс-методом.

Транспортная задача

Классическая транспортная задача формулируется следующим образом:

Имеется m пунктов отправления (производства) A₁, A₂, ..., A_m, в которых расположены запасы некоторого однородного продукта (груза). Объём этого продукта в пункте A_i составляет a_i единиц. Кроме того, имеется n пунктов потребления B₁, B₂, ..., B_n. Объём потребления в пункте B_j составляет b_j единиц. Предполагается, что из каждого пункта отправления возможна транспортировка продукта в любой пункт потребления. Известна также стоимость c_ij перевозки единицы продукта из пункта A_i в пункт B_j.

Требуется составить такой план перевозок, при котором все заявки пунктов потребления полностью выполнялись бы пунктами отправления, а общая стоимость перевозок была минимальной.

При такой постановке данную задачу называют транспортной задачей по критерию стоимости.

В общем виде исходные данные представлены в таблице 2.

Таблица 2

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения

Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой.

Метод минимального элемента.

1. Из распределительной таблицы 2 выбирают наименьшую стоимость и в клетку, которая ей соответствует, помещают меньшее из чисел a_i или b_j (если таких клеток несколько, то выбирают любую);

2. Из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и то и другое;

3. Из оставшейся части таблицы снова выбирают наименьшую стоимость и процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;

4. Рассчитывают транспортные расходы: сумма произведений количества перевезенной продукции на стоимость для занятых клеток.

Метод северо-западного угла.

1. Пользуясь таблицей 2 распределяют груз, начиная с левой верхней, условно называемой северо-западной, клетки (1, 1). Необходимо удовлетворить потребности В₁ за счет поставщика А₁;

2. а). Если b₁> a₁, в клетку (1, 1) записывают a₁ и строку 1 вычеркивают из рассмотрения;

b). Если a₁> b₁, в клетку (1, 1) записывают b₁ и столбец 1 вычеркивают из рассмотрения;

3. а). Если b₁> a₁, ∆ = b₁- a₁ – неудовлетворенные потребности. Спускаются на клетку вниз и сравнивают ∆ с a₂;

b). Если a₁> b₁, ∆ =a₁ - b₁– не вывезенные запасы. Двигаются по строке вправо и сравнивают ∆ с b₂;

4. Необходимо вернуться к пункту 2;

5. Рассчитываются транспортные расходы.

Метод потенциалов.

1. проверяется тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;

2. находится опорный план перевозок путем составления 1-й таблицы одним из способов - северо-западного угла или наименьшей стоимости;

3. проверяем план (таблицу) на удовлетворение системе уравнений и на невыражденность; в случае вырождения плана добавляем условно заполненные клетки с помощью « 0 »;

4. для опорного плана определяются потенциалы u_i и v_j, соответствующие базисным клеткам, по условию:

u_i + v_j = c_ij

Таких уравнений будет m + n - 1, а переменных будет m + n. Для их определения одну из переменных полагают равной любому постоянному значению. Обычно принимают u₁ = 0.

После этого для небазисных клеток опорного плана определяются оценки ,

где

При этом если £ 0, то опорный план оптимален, если же среди окажется хотя бы один положительный элемент, то опорный план можно улучшить.

Улучшение опорного плана осуществляется путем целенаправленного переноса из клетки в клетку транспортной таблицы отдельных перевозок без нарушения баланса по некоторому замкнутому циклу.

Циклом транспортной таблицы называется последовательное соединение замкнутой ломаной линией некоторых клеток, расположенных в одном ряду (строке, столбце), причем число клеток в одном ряду должно быть равно двум.

Каждый цикл имеет четное число вершин, одна из которых в клетке с небазисной переменной, другие вершины в клетках с базисными переменными. Клетки отмечаются знаком «+», если перевозки в данной клетке увеличиваются и знаком «–» в противном случае. Цикл начинается и заканчивается на выбранной небазисной переменной и отмечается знаком «+». Далее знаки чередуются.

Количество единиц продукта, перемещаемого из клетки в клетку по циклу, постоянно, поэтому сумма перевозок в каждой строке и в каждом столбце остаются неизменными. Стоимость всего плана изменяется на цену цикла.

Цена цикла – это стоимость перевозки единицы продукта по циклу с учетом знаков вершин.

Улучшение опорного плана осуществляется путем нахождения цикла с отрицательной ценой.

5. Если критерий оптимальности не выполняется, то переходим к следующему шагу. Для этого:

а) в качестве начальной небазисной переменной принимается та, у которой оценка имеет максимальное значение;

б) составляется цикл пересчета;

12 3 4 5 6 7 Следующая ⇒
Поделиться:

Популярное:
Курсы повышения сексуальной квалификации
МЕЖДУНАРОДНЫЕ ВАЛЮТНО-ФИНАНСОВЫЕ ОТНОШЕНИЯ. ВАЛЮТЫ И ВАЛЮТНЫЕ КУРСЫ

Последнее изменение этой страницы: 2017-03-03; Просмотров: 820; Нарушение авторского права страницы