Лабораторная работа № 16. Алгоритмы сортировок подсчетом, пирамидальных, слиянием, поразрядных
Лабораторная работа № 1. Рекурсивные алгоритмы
Рекурсия - это такая организация работы, при которой функция вызывает сама себя.
| Задание
| Краткие теоретические сведения
| | 1. Изучить использование простых рекурсивных функций на примере программы, представленной в правой части. Определить признак конца ввода чисел, проанализировав текст программы.
Добавить операторы, позволяющие определить, сколько раз функция binPrn вызывает сама себя.
| 
Пример программы перевода десятичного числа в двоичный вид с использованием рекурсии.
| | 2. Выполнить програм-му, разработанную с использованием рекурсии.
Реализовать алгоритм без использования рекурсии.
| 
Пример. Определить, является ли заданная строка палиндромом, т.е. читается одинаково слева направо и справа налево.
Идея решения заключается в просмотре строки одновременно слева направо и справа налево и сравнении соответствующих символов. Если в какой-то момент символы не совпадают, делается вывод о том, что строка не является палиндромом, если же удается достичь середины строки и при этом все соответствующие символы совпали, то строка является палиндромом.
Граничное условие - строка является палиндромом, если она пустая или состоит из одного символа.
| | 3. Выполнить программу, приведенную в правой части. Записать ее условие.
Добавить любое слово в массив w и проанализировать результат работы программы.
Если некоторое слово в массиве w не подходит для решения задачи, то добавить операторы вывода сообщения о том, что его нужно изменить.
|
| #include < iostream>
using namespace std;
char *w[] = { " ПАЛКА", " ЛЯГУШКА", " КАПЛЯ", " КАРТА", NULL };
int TEST(char *s, char *r)
{
int n;
n = strlen(s);
if (n == 0) return 1;
for (; *s! = 0 & & n > 1; s++, n--)
if (strncmp(s, r, n) == 0) return 1;
return 0;
}
int step(char *lw)// текущее слово
{
setlocale (LC_CTYPE, " Russian" );
int n;
for (n = 0; w[n]! = NULL; n++)
if (*w[n]! = 0)
break;
if (w[n] == NULL)// цепочка выстроена
return 1;
| for (n = 0; w[n]! = NULL; n++)
{ char *pw;
if (*w[n] == 0) continue;
pw = w[n]; // пустое слово - пропустить
w[n] = " ";
if (TEST(lw, pw))
{ if (step(pw))//присоединено
{ cout < < pw < < " \n";
return 1;
}
}
w[n] = pw
}
return 0;
}
void main()
{
step(" " );
}
|
|
| | 4. В соответствии со своим вариантом выполнить задания из таблицы, представленной ниже.
| №
| Условие задачи
| Пояснения к алгоритму
| | 1, 2
| Разработать программу, реализующую рекурсивную функцию подсчета количества x(m) разбиений натурального числа m в виде суммы натуральных чисел.
| Для m = 4 разбиения имеют вид: 4, 3+1, 2+2, 2+1+1, 1+1+1+1. Таким образом, x(m) = 5.
Функция подсчета P(m, n) количества разбиений натурального числа m со слагаемыми, не превосходящими n, определяется следующим образом:
При этом x(m) = P(m, m).
| | 3, 4
| Разработать программу, реализующую рекурсивную функцию f(x, n), вычисляющую величину xn/n! при любом вещественном x и любом неотрицательном целом n.
| Для вычисления xn-1/(n-1)! надо рекурсивно обратиться к f(x, n-1), а затем полученную величину умножить на x/n, чтобы получить значение f(x, n).
Функция f(x, n)принимает следующий вид:
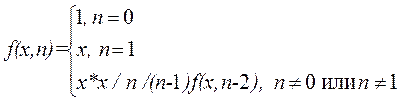
| | 5, 6
| Разработать программу, реализующую рекурсивную функцию подсчета количества всех положительных делителей натурального числа n.
| Рассмотрим более общую задачу подсчета для натурального числа n количества всех его положительных делителей, меньших или равных заданному натуральному числу x.
Пусть dn(n) и dnx(n, x) − функции для решения исходной и обобщенной задач.
Рекурсивную функцию dnx(n, x), по которой последовательно подвергаются испытанию на делители n все числа от 1 до x включительно, можно определить так:
Очевидно, что dn(n) = dnx(n, n).
| | 7, 8
| Задан прямоугольник со сторонами а и b (a, b − натуральные числа). Разбить его на части с помощью квадратов и определить, сколько квадратов получится, если каждый раз выбирается самый большой квадрат.
| Пусть, например a > b. Тогда, отрезав от прямоугольника floor(a/b) квадратов со сторонами длиной b, снова окажемся перед исходной задачей, в которой a = b и b = mod(a, b) (b = a - floor(a / b) × b).
В качестве базы рекурсии можно взять случай b = 0.
Если numsq(a, b) − функция, возвращающая решение задачи при заданных длинах a и b сторон исходного прямоугольника, то
| | 9, 10
| Рекурсивно описать функцию C(m, n), где 0 < = m < = n для биноминального коэффициента Сn.
| Формулы имеют следующий вид:
Сno = Сnn = 1;
Сnm = Сn-1m + Сn-1m-1
| | 11, 12
| Пусть для целых неотрицательных чисел n, m разрешены операции нахождения последующего числа (n + 1) и предыдущего числа n-1 (n > 0).
С помощью рекурсивных функций определить операции нахождения суммы (n + m), разности (n - m), умножения (n × m), возведения в степень n ^ m (n > 0).
| Для суммы a + b очевидно соотношение: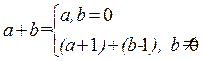 
Оно задает одновременно и базу рекурсии и правило декомпозиции. По нему построена функция, определяющая сложение:
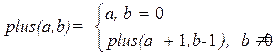Разность: 
Умножение: 
Возведение в степень:
| | 13, 14
| Пусть функция f(x) вещественной переменной x непрерывна на отрезке [a, b] и f(a)× f(b) < 0.
Разработать рекурсивную программу нахождения на отрезке [a, b] какого-либо вещественного корня.
| Для определения корня можно использовать метод деления отрезка пополам. С использованием рекурсии:
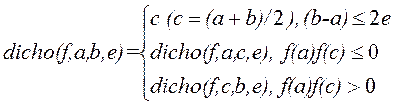Здесь e-заданная точность решения.
| | 15, 16
| Разработать программу, реализующую рекурсивный алгоритм для вычисления значений полиномов по определенной функции.
| Функция имеет следующий вид:
|
5. К номеру своего варианта прибавить число 2 и написать программу для новых исходных данных (для вариантов 15, 16 перейти к вариантам 1, 2).
6. Дополнительные задания.
1. Ввести цифру А, записать в файл все возможные числа, состоящие из цифр, не превышающих или равных A. Количество цифр в числах должно быть равно А. Примечание: использовать дополнительный массив.
2. Рекурсивно определить k-й элемент последовательности целых чисел Люка. Числа задаются рекурсивной формулой: Ln = Ln-1 + Ln-2, где L0 = 2, L1 = 1. То есть последовательность чисел Люка: 2, 1, 3, 4, 7, 11, 18…. Число k вводится с клавиатуры.
3. Задача проведения границы на карте (“создание военных блоков”). Страны на карте заданы матрицей смежности. Если страны i, j имеют на карте общую границу, то элемент матрицы A[i, j] равен 1, иначе 0. Необходимо разбить страны на две группы так, чтобы количество пар смежных стран из противоположных групп было минимальным.
4. Дано n различных натуральных чисел (n = 5). Напечатать все перестановки этих чисел.
5. Последовательность из латинских букв строится следующим образом: на нулевом шаге она пуста, на каждом последующем последовательность удваивается, то есть приписывается сама к себе, и к ней слева добавляется очередная буква алфавита (a, b, c, …).
6. По заданному числу n определить символ, который стоит на n-м месте последовательности, получившейся после шага 26.
В начало практикума
Популярное:
|
