Стационарная теплопроводность через цилиндрическую стенку.
1). Однородная цилиндрическая стенка.
Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d1и внешним диаметром d2 (Рис.9.4).
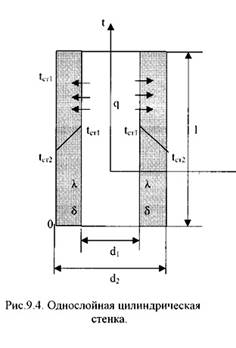
Температуры поверхностей стенки –tст1 и tст2.
Уравнение теплопроводности по закону Фурье в цилиндрических координатах:
Q = - λ ∙ 2∙ π ∙ r ·l· ∂ t / ∂ r (9.24)
или
Q = 2·π ·λ ·l·Δ t/ln(d2/d1), (9.25)
где: Δ t = tст1 – tст2 – температурный напор;
λ – κ оэффициент теплопроводности стенки.
Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:
ql = Q/l =2·π ·λ ·Δ t /ln(d2/d1), [Вт/м]. (9.26)
Температура тела внутри стенки с координатойdх:
tx = tст1 – (tст1 – tст2) ·ln(dx/d1) / ln(d2/d1). (9.27)
2). Многослойная цилиндрическая стенка.
Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).
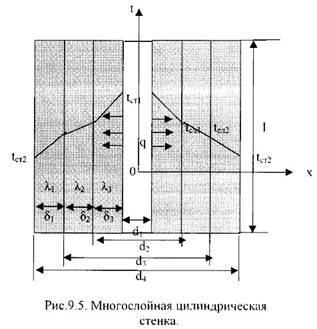
Температура внутренней поверхности стенки –tст1, температуранаружнойповерхности стенки –tст2, коэффициенты теплопроводности слоев -λ 1, λ 2, λ 3, диаметры слоев d1, d2, d3, d4.
Тепловые потоки для слоев будут:
1-й слой
Q = 2·π · λ 1·l·(tст1 – tсл1)/ ln(d2/d1), (9.28)
2-й слой
Q = 2·π ·λ 2·l·(tсл1 – tсл2)/ ln(d3/d2), (9.29)
3-й слой
Q = 2·π ·λ 3·l·(tсл2 – tст2)/ ln(d4/d3), (9.30)
Решая полученные уравнения, получаем для теплового потока через многослойную стенку:
Q = 2·π ·l·(tст1 – tст2) / [ln(d2/d1)/λ 1 + ln(d3/d2)/λ 2 + ln(d4/d3)/λ 3]. (9.31)
Для линейной плотности теплового потока имеем:
ql = Q/l = 2·π · (t1 – t2) / [ln(d2/d1)/λ 1 + ln(d3/d2)/λ 2 + ln(d4/d3)/λ 3]. (9.32)
Температуру между слоями находим из следующих уравнений:
tсл1 = tст1 – ql·ln(d2/d1) / 2·π ·λ 1 . (9.33)
tсл2 = tсл1 – ql·ln(d3/d2) / 2·π ·λ 2 . (9.34)
Стационарная теплопроводность через шаровую стенку.
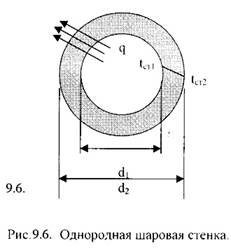
Пусть имеется полый шар (Рис.9.6) – внутренний диаметр d1, внешний диаметрd2, температура внутренней поверхности стенки –tст1, температуранаружнойповерхности стенки –tст2, коэффициент теплопроводности стенки -λ .
Уравнение теплопроводности по закону Фурье в сферических координатах:
Q = - λ ·4·π ·r2· ∂ t / ∂ r (9.35)
или
Q =4·π ·λ ·Δ t/(1/r2 - 1/r1) =2·π ·λ ·Δ t/(1/d1 - 1/d2) =
= 2·π ·λ ·d1·d2·Δ t /(d2 - d1) = π ·λ ·d1·d2·Δ t / δ (9.36)
где: Δ t = tст1 – tст2 – температурный напор;
δ –толщина стенки.
Тема 10. Конвективный теплообмен.
Факторы, влияющие на конвективный теплообмен.
Конвективным теплообменом называется одновременный перенос теплоты конвекцией и теплопроводностью.
В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.
Основными факторами, влияющими на процесс теплоотдачи являются следующие:
1). Природа возникновения движения жидкости вдоль поверхности стенки.
Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция).
Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция).
2). Режим движения жидкости.
Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным.
Беспорядочное, хаотическое, вихревое движение называется турбулентным.
3). Физические свойства жидкостей и газов.
Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (l), удельная теплоемкость (с), плотность (ρ ), κ коэффициент температуропроводности (а = λ /cр·ρ ), коэффициент динамической вязкости (μ ) или кинематической вязкости (ν = μ /ρ ), тε мпературный коэффициент объемного расширения (β = 1/Т).
4). Форма (плоская, цилиндрическая), размеры и положение поверхности (горизонтальная, вертикальная).
Закон Ньютона-Рихмана.
Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, которая гласит, что количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (t'ст) и окружающей среды (t'ж):
Q = α · (t'ст - t'ж)·F, (10.1)
или
q = α · (t'ст - t'ж), (10.2)
где: коэффициент теплоотдачи [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:
α = f1(Х; Ф; lo; xc; yc; zc; wo; θ; λ; а; ср; ρ; ν; β ), (10.3)
где: Х – характер движения среды (свободная, вынужденная);
Ф – форма поверхности;
lo – характерный размер поверхности (длина, высота, диаметр и т.д.);
xc; yc; zc – координаты;
wo – скорость среды (жидкость, газ);
θ = (t'ст - t'ж) – температурный напор;
λ – коэффициент теплопроводности среды;
а – коэффициент температуропроводности среды;
ср –изобарная удельная теплоемкость среды;
ρ –плотность среды;
ν – коэффициент кинематической вязкости среды;
β – температурный коэффициент объемного расширения среды.
Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.
Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.
Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.
Популярное:

