Применение методов дискретной математики в экономике.

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом рассмотрения в дискретной математике. К ним относятся методы, основанные на теоретико-множественных представлениях, графы, алгоритмы формальные системы, математическая логика.

В экономике существует множество отраслей, использующих методы дискретной математики. Это и эконометрика, и логистика, и математическое моделирование. Так, в эконометрике булевские переменные применяются в исследовании регрессионных моделей с переменной структурой и в построении регрессионных моделей по неоднородным данным. В этом случае рассматривается лишь одно уравнение регрессии, куда вводятся булевские переменные, которые характеризуют изучаемый фактор. Данный метод удобен для выявления зависимости модели от некоторого фактора.

Теория графов широко используется в логистике для описания потоков, задания маршрутов. Так схему дорог удобнее представить в виде ориентированного графа, и известными нам методами выбрать кратчайший путь. В настоящее время, прокладывая маршрут, нельзя не брать во внимание и пропускную способность магистралей, интерпретируя маршруты в графы, можно получить экономически выгодное решение.

При помощи теории нечетких множеств, методом нечеткого предпочтения, можно выбрать конкурентоспособный товар или услугу. Поэтому, данная теория применяется в маркетологии, при исследовании рынков различных экономических благ.

Раздел 3. Основы математического анализа

Дифференциальное исчисление.

Общая схема исследования функции и построения ее графика

1. Найти область определения функции. Выделить особые точки (точки разрыва).

2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

3. Найти точки пересечения с осями координат

4. Установить, является ли функция чётной или нечётной.

5. Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).

6. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.

7. Найти точки перегиба и интервалы выпуклости-вогнутости.

8. Найти наклонные асимптоты функции.

9. Построить график функции.

Пример:

Исследовать функцию методами дифференциального исчисления и построить график y = x³+6x²+9x+2

РЕШЕНИЕ:

1) Область определения функции – вся числовая прямая, то есть

D (y) = (− ∞; +∞ ).

Точек разрыва нет, вертикальных асимптот нет.

2) Точки пересечения с осями координат:

Ox: найти затруднительно

Oy: x=0⇒ 0³+6*0²+9*0+2=2 ⇒ Точка (0; 2)

3)Функция общего вида, так как

y(-x) = -x³+6x²-9x+2≠ ±y(x)

4) Экстремумы и монотонность. Вычисляем первую производную:

y'=3x²+12x+9

Находим критические точки: y'=0; 3x²+12x+9=0; x₁=-1; x₂=-3.

Исследуем знак производной на интервалах,

на которые критические точки делят область определения функции.

y' + - +

y -3 -1 x

Функция возрастает на интервалах (− ∞ ; -3), (-1; +∞ ), убывает на интервале

(-3; -1). Функция имеет минимум в точке x = -1, y(-1) =-2, функция имеет максимум в точке x = -3, y(-3)=2.

5) Выпуклость и точки перегиба. Вычисляем вторую производную.

y''=(3x²+12x+9)'=6x+12

Находим критические точки: y''=0; 6x+12=0; x=-2.

Исследуем знак производной на интервалах, на

которые критические точки делят область определения функции.

y'' - +

y -2 x

Функция выпукла вверх на интервале (− ∞; -2), выпукла вниз на интервале

(-2; +∞ ). Точка перегиба: x =-2, y(-2) = 0.

6) Асимптоты.

Так как = =∞ , асимптот нет.

7) Строим график функции.

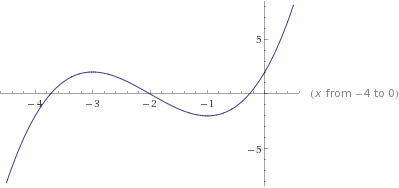
Интегральное исчисление.

1.Основные правила интегрирования

1. Если

то

где

– произвольная постоянная. 2.

где

– постоянная. 3.

2.Таблица основных неопределенных интегралов

1.. 2. 3.. 4. 5. 6. 7. 8. 9. 10. 11. 12.

3.Непосредственное интегрирование

Отыскание неопределенного интеграла с помощью таблицы, правил и тождественных преобразований называют непосредственным интегрированием. Пример:

)dx = 2

dx -

dx + 3

= 2

+3 arcsin x + C При интегрировании использованы правила 2 и 3, а также табличные формулы 2, 4, 6, 11.

4.Метод подстановки (замена переменной интегрирования)

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а)

где

– монотонная, дифференцируемая функция; б)

– новая переменная. В первом случае формула замены переменной имеет вид:

. (1) Во втором случае:

. (2) В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой. Пример 1. Вычислить интеграл:

Решение. Сделаем замену переменных t=x+1 и найдем дифференциал от обеих частей, тогда dt = (x+1)'dx ⇒ dt= dx Подставляя все в исходный интеграл, получим:

+C =

+C, где C - const. Здесь заключительное действие - это обратная замена переменных. В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.

Пример 2:

(положим t = 2x+3, тогда x= t- , dx = dt)

= =- +C= =- +C

Пример 3:

dx= (положим t= x²+25, тогда dt = 2x dx, x dx= dt) = * dt= dt= +C = +C = +C = +C

Определенный интеграл.

Если существует определенный интеграл от функции f(x), то в этом случае функция называется интегрируемой на отрезке .

Для интегрируемости функции на отрезке достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.

Если функция непрерывна на , то от нее существует неопределенный интеграл

и имеет место формула

т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.

Формула

называется формулой Ньютона-Лейбница.

Пример 1:

Необходимо найти определенный интеграл

Имеем:

Таким образом искомый интеграл равен 6.

Пример 2:

Вычислить интеграл:

Решение:

=( 3 + 4 +5x) = +2 -

- ( +2 26- 8=18.

Приложение определенного интеграла в экономике

Интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике.

Задача. Известно, что спрос на некоторый товар задается функцией p = 4 – q², где q – количество товара (в шт.), p – цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p* = q* = 1. Определите величину потребительского излишка.

Решение.

⇐ Предыдущая 1 234 Следующая ⇒