Законы идеального газа. Макроскопические параметры. Уравнение состояния.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона —Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

§ — давление,

§ — молярный объём,

§ — универсальная газовая постоянная

§ — абсолютная температура, К.

Так как 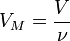, где 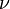— количество вещества, а , где — масса, — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

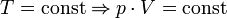— закон Бойля — Мариотта.

— Закон Гей-Люссака.

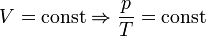— закон Шарля (второй закон Гей-Люссака, 1808 г.)

Законы идеального газа

Закон Бойля-Мариотта устанавливает зависимость между абсолютным давлением и удельным объемом ν газа при постоянной температуре:
P₁v₁ = P₂v₂ = const (2.14)
Закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:
V_t = V₀ (1 + β _pt) = V₀(1 + t/273, 15) (2.15)
или при постоянном объеме:
P_t = Р₀ (1 + β _pt) = Р₀ (1 + t/273, 15) (2.16)
где V_t, V₀ — объемы газа при t°С и 0°С; p_t и р₀ — давление газа (абсолютное) при t°С и 0°С; β _p — коэффициент объемного расширения идеального газа, равный коэффициенту изменения давления:
β _p = 1/273, 15 = 0, 00366 (2.17)
Подставив значения β _p и заменив температуру практической шкалы t абсолютной термодинамической Т, получим:
V₁/V₂ = Т₁/Т₂ (2.18)
р₁/p₂ = Т₁/Т₂ (2.19)
На основании законов Бойля-Мариотта и Гей-Люссака получаем уравнения, связывающие объем и плотность с температурой и давлением:
V₁ = V₂ (p₂Т₁)/(р₁Т₂) (2.20)
v₂ = v₁ (р₂Т₁)/(р₁Т₂) (2.21)
р₁ = p₂ (р₁T₂)/(p₂T₁) (2.22)
Приведение газа к нормальным условиям при рабc = 101, 3 кПа и t = 0°С (Т = 273, 15 К) и от нормальных условий к заданным осуществляется по уравнениям:
V_н = 2, 6965V (Р_абс/Т); Р_н = 0, 3708р (Т/р_абс); (2.23)
V = 0, 3708V_н (Т/р_абс); р = 2, 6965р_н (р_абс/Т) (2.24)
Приведение газа к стандартным условиям [р_абс = 101, 3 кПа и t = 20°C (Т = 293, 15 К)] и обратно выполняется по уравнениям: V_ст = 2, 894V (Р_абс/Т); Р_ст = 0, 3455р (Т/р_абс) (2.25)
V = 0, 3455V_ст (Т/р_а

_бс); р = 2, 894р_ст (р_абс/Т) (2.26)
где V_н, ρ _н — объем (м³) и плотность (кг/м³) газа при р_абс = 101, 3 кПа и Т = 273, 15 К; V, ρ — объем и плотность газа при р_абс, кПа, и Т, К; V_ст, ρ _ст — объем и плотность газа при рабс= 101, 3 кПа и Т = 293, 15 К.
Закон Авогадро: различные газы, занимающие одинаковые объемы при равных условиях (одинаковых давлении и температуре), содержат одинаковое число молекул. Это число для 1 грамм-молекулы (1 моль) любого газа составляет около 6, 025•10²³ и называется числом Авогадро. Таким образом, массы различных газов, занимающие одинаковый объем при равных условиях, соотносятся между собой как их молекулярные массы. Средний объем 1 моль двухатомных газов и метана равен 22, 4 л, соответственно, объем 1 кмоль сжиженных газов приблизительно равен 22 м³.
Основные значения молекулярных масс и молярных объемов, а также плотности газов приведены в табл. 2.4. Одно из следствий закона Авогадро: произведение удельного объема на молекулярную массу есть величина постоянная, равная молярному объему.
Объединив законы Бойля-Мариотта и Гей-Люссака, получим уравнение состояния идеального газа:
P_a6cv/T = R = сonst (2.27)
где v — удельный объем газа; R — универсальная газовая постоянная.
Газовая постоянная — физическая величина, равная работе изменения объема, совершаемой 1 кг идеального газа в изобарическом процессе при изменении температуры на 1°С (1 К). Единицы газовой постоянной — кг•м/(кг•°С); ккал/(кг•°С); Дж/(кг•К). 1 Дж/(кг•К) = 0, 238846 кал/(кг•°С) = 0, 10197 кг•м/(кг•°С).
Уравнение относится к 1 кг газа. Так как удельный объем v = V/m, то для произвольного количества газа уравнение примет вид:
Р_абсV = mRT (2.28)
или для смеси газов
Р_абcV = m_смRT (2.28)
где m_см — масса смеси, кг.
Для 1 кмольV_м в соответствии с законом Авогадро постоянная имеет одно и то же значение для всех газов и называется универсальной газовой постоянной:
Р_абc v_м = MRT (2.29)
Так как VM = vM, то
Р_абc v_м = MRT (2.30)
Последние уравнения, отображающие параметры состояния любого газа, носят название уравнений Менделеева. Значение и единица универсальной газовой постоянной зависят от того, в каких единицах выражены давление и объем газа.
При р_абс = 10330 кгс/м², VM = 22, 0 м³/кмоль и Т = 273, 15 К газовая постоянная для 1 кмоль MR = 831, 96 кгс•м/(кмоль•°С) = 8153, 21 Дж/(кмоль•К).
Для двухатомных газов и для метана — 847, 1 кгс•м/(кмоль•°С) = 8301, 6 Дж/(кмоль•К). По универсальной газовой постоянной и по молекулярной массе определяется удельная газовая постоянная любого углеводородного газа:
R = 8153, 21/М (2.31)

МАКРОСКОПИЧЕСКИЕ ПАРАМЕТРЫ – это физические величины, характеризующие макроскопическое тело (или его макроскопические части) в целом, без учета его молекулярного строения. Макроскопическими являются такие параметры, как температура, давление, объем, внутренняя энергия, энтропия и др. Иначе эти параметры называются термодинамическими.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть может, еще некоторыми другими).

Величины, характеризующие макросостояние, называются макроскопическими параметрами. Те из них, которые характеризуют внутреннее состояние системы, называются внутренними параметрами, а те, которые описывают внешнюю среду (внешние тела, поля), — внешними параметрами.

Смысл разделения на микро- и макросостояния состоит в следующем. Хаотическая динамика на микроскопическом уровне (молекулярный хаос) проявляется как упорядоченное изменение состояния на макроскопическом уровне. Точное описание поведения системы на языке микросостояний чрезвычайно сложно, если вообще возможно. Вместе с тем достаточно полное описание макроскопического поведения системы большого числа частиц может быть получено с помощью небольшого числа макроскопических параметров — давления Р, температуры Т, объема V и, быть может, еще нескольких других существенных характеристик. Если не интересоваться внутренним строением вещества, то достаточно ограничиться описанием на уровне макросостояния. При необходимости можно уточнить это описание, вводя в рассмотрение те или иные дополнительные параметры (например, те из них, которые характеризуют форму тела, его заряд, магнитный момент и т. д.).

Уравне́ ниесостоя́ ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

Уравнение состояния системы не содержится в постулатах термодинамики и не может быть выведено из неё. Оно должно быть взято со стороны (из опыта или из модели, созданной в рамках статистической физики). Термодинамика же не рассматривает вопросы внутреннего устройства вещества.

Заметим, что соотношения, задаваемые уравнением состояния, справедливы только для состояний термодинамического равновесия.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться: