ВОПРОС 21. Металлические фермы. Классификация. Расчет сжатых и растянутых стержней. ⇐ ПредыдущаяСтр 7 из 9Следующая ⇒ Фермой называется система стержней соединенных между собой в узлах и образующих геометрически неизменяемую конструкцию. Фермы экономичнее балок по расходу стали, но более трудоемки в изготовлении. Эффективность ферм по сравнению со сплошностенчатыми балками тем больше, чем больше пролет и меньше нагрузка. Фермы бывают плоскими (все стержни лежат в одной плоскости) и пространственными. Плоские фермы воспринимают нагрузку, приложенную только в их плоскости, и нуждаются в закреплении их связями. Пространственные фермы образуют жесткий пространственный брус, воспринимающий нагрузку в любом направлении (рис.9.1).   Основными элементами ферм являются пояса, образующие контур фермы, и решетка, состоящая из раскосов и стоек (рис. 9.2). Соединение элементов в узлах осуществляется путем непосредственного примыкания одних элементов к другим (рис 9.3 а) или с помощью узловых фасонок (рис. 9.3 б).   Рис. 9.2. Элементы ферм 1 – верхний пояс; 2 – нижний пояс; 3 – раскосы; 4 - стойки   Рис. 9.3. Узлы ферм а – с непосредственным примыканием элементов; б – на фасонках Фермы имеют разную конструкцию в зависимости от назначения, нагрузок и классифицируются по различным признакам: по статической схеме – балочные (разрезные, неразрезные, консольные); арочные, рамные, комбинированные (рис. 9 4);   Рис.9.4. Системы ферм а – балочная разрезная; б – неразрезная; в, е – консольная; г – арочная; д – рамная; ж - комбинированная по очертанию поясов – с параллельными поясами, трапециевидные, треугольные, полигональные, сегментные (рис. 9.5); по системе решетки – треугольная, раскосная, крестовая, ромбическая и др. (рис.9.6); по способу соединения элементов в узлах – сварные, клепанные, болтовые; а – сегментное; б – полигональное; в – трапецеидальное; г – с параллельными поясами; д-и - треугольное Рис. 9.5. Очертания поясов ферм по величине максимального усилия – легкие – одностенчатые с сечениями из прокатных профилей (усилие N кН) и тяжелые – двухступенчатые с элементами составного сечения ( N > 300кН). Промежуточными между фермой и балкой являются комбинированные системы, состоящие из балки, подкрепленной снизу шпренгелем или раскосами либо аркой (сверху). Подкрепляющие элементы уменьшают изгибающий момент в балке и повышают жесткость системы (рис.9.4, ж). Комбинированные системы просты в изготовлении (имеют меньшее число элементов) и рациональны в тяжелых конструкциях, а также в конструкциях с подвижными нагрузками. Эффективность ферм м комбинированных систем можно повысить, создав в них предварительное напряжение. В фермах подвижных крановых конструкций и покрытий больших пролетов, где уменьшение веса конструкции дает большой экономический эффект, применяют алюминиевые сплавы. Рис. 9.6. Системы решетки ферм

а – треугольная; б – треугольная с дополнительными стойками; в – раскосная с восходящими раскосами; г – раскосная с нисходящими раскосами; д – шпренгельная; е – крестовая; ж – перекрестная; и – ромбическая; к - полу раскосная

 

ВОПРОС 22.Деревянные фермы. Классификация, конструкция и расчет.
Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирами. Фермы относятся к классу сквозных конструкций, в которых пояса соединены между собой решеткой, состоящей из отдельных стержней – раскосов и стоек. Фермы применяются в покрытиях производственных и гражданских зданий в тех случаях, когда балки сплошного сечения оказываются экономически невыгодными. Применение решетки уменьшает расход материала на конструкции, но увеличивает трудоемкость изготовления.

Классификация. По конструктивной схеме различают: балочные фермы и распорные-арочные; по очертанию пояса: треугольные фермы, трапециевидные, многоугольные, сегментные, с параллельными поясами; по материалу: из цельной древесины, из клееной древесины, металлодеревянные, из фанерных труб, стеклопластикодеревянные фермы; по типу узловых соединений: на лобовых врубках, на стальных цилиндрических нагелях, на клеестальных шайбах, на зубчатых шипах на клею.

Расчет. 1) Определение узловых нагрузок, действующих на ферму, 2) Определение усилий в стержнях фермы, 3) Подбор поперечного сечения нижнего пояса, 4) Подбор поперечного сечения верхнего пояса, 5) Подбор сечений раскосов, 6) Подбор сечений стоек, 7)Расчет и конструирование опорного узла, 8) Расчет и конструирование промежуточных узлов.

 

 

Для определения усилий в стержнях фермы методом сечений необходимо:

1) Сечение проводить таким образом, чтобы оно

· пересекало ось стержня, в котором определяется усилие;

· пересекало по возможности не более трех стержней;

· разделяло ферму на две части.

2) Продольные усилия в стержнях направлять в положительном направлении, т.е. от узла.

3) Выбирать такие уравнения равновесия для части фермы, которые включали бы лишь одно искомое усилие. Такими уравнениями являются, например,

· сумма моментов относительно точки, в которой пересекаются лини действия усилий в стержнях ферм, разрезанных сечением; такие точки принято называть моментными;

· сумма проекций сил на вертикальную ось для раскосов ферм с параллельными поясами.

4) Для определения усилий в стойках вырезать узлы, если в них сходится не более трех стержней.

5) Для упрощения определения плеч внутренних усилий относительно моментной точки при составлении уравнений моментов при необходимости заменять искомые усилия их проекциями на взаимно перпендикулярные оси.

2.6.2. Определение усилий в стержнях фермы.

Для определения усилий в стержнях фермы необходимо:

· определить реакции опор;

· методом сечений определить требуемые усилия;

· произвести проверку полученных результатов.

Реакции опор в простых балочных фермах, показанных на рис.2.37, определяются также как в однопролетных балках с помощью уравнений вида

, .

Для проверки реакций опор используем уравнение

.

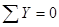Рассмотрим алгоритм расчета на конкретном примере.

Дана расчетная схема фермы (рис.2.38).

Рис.2.38

Требуется определить усилия в стержнях 4-6, 3-6, 3-5, 3-4, 7-8.

Решение задачи.

1) Определяем реакции опор.

Для этого используем уравнение равновесия:

 

, .

 

Записываем уравнения, используя принятое правило знаков:

 

 

Решая уравнения, находим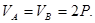

Проверяем реакции опор по уравнению .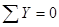

2) Определяем усилия в стержнях фермы.

а) Усилия в стержнях 4-6, 3-6, 3-5.

Для определения усилий в указанных стержнях разрезаем ферму сечением а-а на две части и рассматриваем равновесие левой части фермы (рис.2.39.

Рис.2.39

К левой части фермы прикладываем реакцию опоры , силу , действующую в узле 4, и искомые усилия в стержнях фермы 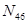, , 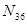. Эти усилия направляем вдоль соответствующих стержней в сторону от узла, то есть в положительном направлении.

Для определения усилий 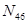, , 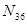можно использовать следующую систему уравнений:

 

, , .

 

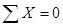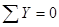Но в этом случае получим совместную систему уравнений, в которые будут входить все искомые усилия.

⇐ Предыдущая123456789Следующая ⇒

Поделиться: