
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ЛИНЕЙНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКАСтр 1 из 5Следующая ⇒
ЛИНЕЙНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА РАСЧЁТ ПРОСТЕЙШИХ ЦЕПЕЙ
ЗАДАЧА 3.1. На рис. 3.2 приведены осциллограммы напряжения и тока. Требуется записать выражения для их мгновенных значений, определить действующие значения напряжения и тока. Решение По осциллограммам определяем период колебаний Т = 20 мс, следовательно, час-тота f =1/T = 50 Гц, а угловая частота w = 2pf = 314 рад/с. Начальные фазы напряжения и тока в градусах, соответственно: ψ u = -t1× (360/T) = 1, 67× (360/20) = 30°, ψ i = -t2× (360/T) = -2, 5× (360/20) = -45°, Амплитуды: Um = 400 B, Im = 1, 5 A. Следовательно, u(t) = 400× sin(314t+30°) B, i(t) = 1, 5× sin(314t-45°) A. Действующие значения: U = ЗАДАЧА 3.2. Цепь r, L с параметрами r = 35 Ом, L = 80 мГн питается от источника синусоидального напряжения частоты f = 50 Гц. Амплитудное значение напряжения питания Um= 200 B, а начальная фаза ψ u = -20°. Рас-считать мгновенное и действующее значения тока. Построить векторную диаграмму цепи. Найти активную, реактивную и полную мощности цепи. Построить треугольник мощностей. Решение Приведём расчётную схему цепи (рис. 3.3, а).
Запишем мгновенное значение приложенного к цепи r, L напряжения: u(t) = Um× sin(ω t + ψ u)= 200× sin(ω t – 20°) B. Круговая частота ω = 2pf = 2p× 50 = 314 рад/с. Индуктивное сопротивление цепи xL= ω L = 314× 80× 10 -3 = 25, 12 Ом. По второму закону Кирхгофа для контура цепи u = ur + uL или в век-торной форме u = ur + uL. На основании этого уравнения строится вектор-ная диаграмма напряжений (рис. 3.3, б). Треугольник сопротивлений цепи приведен на рис. 3.3, в. Это – прямо-угольный треугольник, из которого получаем полное сопротивление цепи Z = и угол сдвига фаз между током и напряжением j = arctg По закону Ома для амплитудных значений Im= Начальная фаза синусоиды тока ψ i = ψ u – j = -20° – 35, 67°= -55, 67°. Мгновенное значение искомого тока i(t) = 4, 64× sin(314t – 55, 67°) A. Действующее значение тока I = Действующие значения напряжений на участках: - на резисторе ur = I× r = 3, 28× 35 = 115 B; - на индуктивности uL = I× xL = 3, 28× 25, 12 = 82, 4 B; - на входе цепи (напряжение сети) u = Активная мощность цепи P = U× I× cosj = I 2× r = 3, 282× 35 = 376, 5 Bт. Реактивная мощность Q= U× I× sinj = I 2× xL = 3, 282× 25, 12 = 270, 2 вар. Полная мощность S = U× I = 141, 4× 3, 28 = 464 BA. Треугольник мощностей приведен на рис. 3.3, г. Отметим, что на основании любого из треугольников рис. 3.3 можно рассчитать коэффициент мощности cosj = полученный ранее на основании треугольника сопротивлений цепи. ЗАДАЧА 3.3. В цепи рис. 3.4, а протекает синусоидальный ток i(t) = 10× sin(ω t +15°) A частоты f = 400 Гц. Активные сопротивления r1 = = 10 Ом, r2 = 20 Ом, ёмкость С = 10 мкФ.
Рассчитать мгновенное значение напряжения сети u(t) и напряжения на конденсаторе uС(t). Найти показания вольтметра и ваттметра. Построить векторную диаграмму цепи. Решение Ёмкостное сопротивление xС = Амплитудное значение напряжения на ёмкости uCm = Im× xC = 10× 39, 81 = 398, 1 B. Действующие значения I = Действующие значения напряжений на активных сопротивлениях ur1= I× r1 = 7, 07× 10 = 70, 7 B, ur2= I× r2 = 7, 07× 20 = 141, 4 B. II-й закон Кирхгофа в векторной форме при одном токе I имеет вид ur1+ur2+uC = u, в соответствии с которым построена векторная диаграмма цепи (рис. 3.4, б). Из прямоугольного треугольника напряжений (наружный треугольник) u = j = arctg Мгновенное значение напряжения сети u(t)= Um× sin(ω t+ψ i+j) = u× Напряжение на конденсаторе по фазе отстаёт от тока на 90°, его мгновенное значение uC(t)= 398, 1× sin(ω t – 75°) B. Напряжение на участке r2-C, приложенное к ваттметру и вольтметру, рассчитаем по треугольнику напряжений u2-ur2-uC: u2 = uW = Вольтметр схемы рис. 3.4, а измеряет действующее значение напряже-ния u2= 315 B. Показание ваттметра: PW = uW × IW × cos В нашем примере IW = I, поэтому PW = u2× I× cosj 2 = I× (u2× cosj 2)= I× ur2= I× I× r2 = I 2× r2 = P2 – активная мощность, потребляемая сопротивлением r2, и P2 = 7, 072× 20 = 1000 Bт.
Решение Ток цепи I, измеряемый амперметром А: I = Угол сдвига фаз цепи jвх = arctg Вольтметр V измеряет входное напряжение U = 50 В. Напряжение на катушке измеряется вольтметром V1: Uк = Напряжение на реостате: UR = I× R = 5× 2 = 10 В, напряжение на конденсаторе UC = I× хС = 5× 14 = 70 В. Векторная диаграмма цепи построена на рис. 3.5, б. Ваттметр измеряет активную мощность цепи Р = U× I× cosjвх = I 2× (rк + R) = 52× (4 + 2) = 150 Вт. Обращаем внимание на то, что в последовательной цепи при наличии разнородных реактивных элементов (индуктивного и ёмкостного), напряже-ние на реактивном элементе может быть больше напряжения сети: UC =70 В > U = 50 В. ЗАДАЧА 3.5. В условиях задачи 3.4 при неизменном напряжении сети и параметрах rк, хк, R в широких пределах изменяется сопротивление кон-денсатора хС(0¸ ¥ ). Построить резонансные кривые I(хС), UL(хС), UС(хС). Решение Ток в последовательной цепи рис. 3.5, а: I = напряжение на индуктивности UL = I× хL = I× 6 В, напряжение на ёмкости UС = I× хС = Результаты расчёта резонансных кривых сведены в табл. 3.3. Таблица 3.3
В табл. 3.3 выделена колонка, когда хк=хС=6 Ом и в цепи наступает резонанс напряжений UL=UС. При этом входное сопротивление цепи минимальное Zвх min = rк+R = 6 Ом, а ток максимальный Imax = Кривая напряжения UL повторяет по форме кривую тока, так как хк=const, и тогда ULmax = Imax× хк = 8, 33× 6 = 50 В. Найдём максимальное значение UСmax в зависимости от хС, исследовав кривую UС(хС) на максимум. Координата хС при UС = UСmax определится уравнением
(rк+R)2 + хк2 – 2 хк хС + хC2 + хк хС – хC2= 0, откуда
Резонансные кривые приведены на рис. 3.6. ЗАДАЧА 3.6. Определить показания приборов в схеме рис. 3.7, а, мгновенное значение тока i1 в неразветвлённой части схемы, построить векторную диаграмму, если:
u(t)= 200× sin(ω t+25°) В, r = 50 Ом, хС = 50 Ом. Решение Приборы реагируют на действующие значения величин. Действующие значения токов параллельных ветвей I2= I3= Так как ток в активном сопротивлении i3 совпадает по фазе с напряжением, ток в ёмкости опережает по фазе напряжение на 90°, а в соответствии с І законом Кирхгофа i1 = i2 + i3, то треугольник токов на векторной диаграмме (рис. 3.7, б) прямоугольный, откуда I1= угол сдвига фаз между током i1 и напряжением u на входе схемы отрицательный и равен j = -arctg Мгновенное значение тока i1(t) = I1m× sin(ω t +yu – j) = 4 Показания амперметров A1 ® I1= 4 А, A2 ® I2= 2, 83 А, A3 ® I3= 2, 83 А. Показание ваттметра PW = uW × IW × cos Заметим, что по схеме рис. 3.7, а ваттметр измеряет активную мощность части цепи, находящейся справа от ваттметра. Но по закону Джоуля-Ленца в этой части расходуется мощность только в активном сопротивлении r, причём Р3= I32× r =
ЗАДАЧА 3.7. Найти показания приборов в схеме рис. 3.8, а, построить векторную диаграмму, если u = 200 В, r1= 30 Ом, х1= 40 Ом, r2= 50 Ом.
Решение Токи параллельных ветвей рассчитаем по закону Ома и определим соответствующие показания амперметров: I2= I1= Ток i2 в активном сопротивлении совпадает по фазе с напряжением u, ток i1 отстаёт на угол j 1, так как в этой ветви имеется индуктивность, а сам угол j 1 определим из треугольника сопротивлений этой ветви j 1 = arctg При этом cosj 1 = Всё изложенное учтено при построении векторной диаграммы цепи (рис. 3.8, б). В рассматриваемом примере получен косоугольный треугольник токов I1, I2, I. Задача расчёта косоугольного треугольника токов сводится к прямоугольному, если систему векторов токов спроецировать на два взаимно перпендикулярных направления: на направление вектора напряжения (проекции векторов токов называются активными составляющими) и направление, перпендикулярное вектору напряжения параллельного участка (проекции называются реактивными составляющими). При этом I2a = I2 = 4 A, I2p = 0, I1a = I1× cosj1 = 4× 0, 6 = 2, 4 A, I1p = I1× sinj1 = 4× 0, 8 = 3, 2 A. Из наружного прямоугольного треугольника определяется суммарный ток параллельных ветвей, измеряемый амперметром А: I = Далее j = arctg cosj = Показание ваттметра PW = u× I× cosj = u× SIа= 200× 6, 4 = 1280 Вт – это активная мощность источника РГ. Суммарная активная мощность потребителей рассчитывается по закону Джоуля-Ленца: SРП = I12× r1 + I22× r2 = 42× 30 + 42× 50 = 1280 Вт. Так как для схемы РГ = SРП, то баланс активных мощностей сходится. Реактивные мощности: - генератора QГ = u× I× sinj = u× Ip= 200× 3, 2 = 640 вар; - потребителей SQП = I12× х1 = 42× 40 = 640 вар, то есть выполняется и баланс реактивных мощностей.
3.2.2. Задачи для самостоятельного решения ЗАДАЧА 3.8. Действующее значение синусоидального напряжения u =220 В. Определите его среднее значение.
ЗАДАЧА 3.9. Лампа накали-вания с номинальными данными РЛн = 15 Вт; uЛн = 127 В включена последовательно с конденсатором С = 2 мкФ и на вход этой цепи подано напряжение u = 220 В. Определить напряжение на лампе. Сделать вывод о том, будет ли лампа нормально светить или нет. Ответ: UЛ = 123, 1 В; да, будет.
Ответ: UV1 = 215, 4 В; UV2 = 0.
ЗАДАЧА 3.11. В схеме рис. 3.10 известно: u = 50 В; I = 0, 13 А; Ir = 0, 12 А. Определить величину индуктивности L. Ответ: L = 0, 318 Гн.
ЗАДАЧА 3.12. Три однофазных двигателя включены параллельно и к ним подведено напряжение u = 400 В. Паспортные данные двигателей:
Ответ: I = 14, 85 А.
ЗАДАЧА 3.13. В схеме рис. 3.11 требуется определить показание амперметра, если u = 100 В, r1= 3 Ом, r2= 8 Ом, r3= 10 Ом, хL1= 4 Ом, хL2= 5 Ом, хC = 6 Ом. Ответ: I = 42, 4 А.
Определить параметры схемы r1, хL, r2, хС. Построить векторную диаг-рамму цепи. Построить резонансную кривую uL(хL) при изменении хL(0…¥ ).
r2 = 10 Ом, хС = 49 Ом.
Задачи повышенной сложности ЗАДАЧА 3.15. По показаниям приборов цепи рис. 3.13 определить параметры её элементов, если V ® 100 B; V1 ® 20 B; W ® 80 Bт; А ® 2 А.
ЗАДАЧА 3.16. В схеме рис. 3.14 определить показание ваттметра, если u = 100 В, а показания приборов: А ® 1 А; V1 ® 150 B; V2 ® 100. Ответ: Р = 198, 4 Вт.
ЗАДАЧА 3.17. В схеме цепи рис. 3.15 задано: r1= r3; Р = 300 Вт; I1 = 5 Ответы: I = 15 А, L = 6, 37 мГн, С = 796, 3 мкФ.
ЗАДАЧА 3.18. В схеме рис. 3.16 известно: u = 10 В; хL = 6 Ом; Р = 5 Вт. Определить сопротивление R. Решение Используем следующие соотношения: Р = R× I 2 ; u = I× Тогда: I 2 = Отсюда R1, 2 = Задача имеет два ответа R1= 18 Ом и R2 =2 Ом.
3.3.1. Типовые примеры ЗАДАЧА 3.19. К цепи рис. 3.17 подведено напряжение u = 220 В. До подключения ёмкости С приборы показывали: А ® I=2 А; W ® P=40 Вт. Требуется определить минимально возможное показание амперметра после подключения ёмкости, а также величину последней. Решение До подключения ёмкости, используя показания приборов, определяем полное, активное и индуктивное сопротивления ветви с r, L: Z = xL = Минимальное значение тока в неразветвлённой части цепи будет иметь место при резонансе токов в цепи после подключения ёмкости, и в этом случае ток I будет иметь только активную составляющую: I = Ia = U× g, где g – активная проводимость всей цепи, равная активной проводимости ветви r, L, а именно: g = Тогда I = U× g = 220× 2, 26× 10 -4 = 0, 182 А. Величину ёмкости определим из условия, что её реактивная проводимость должна равняться реактивной проводимости ветви r, L, т.е. wС =
ЗАДАЧА 3.20. Для схемы (рис. 3.18, а) определить токи во всех ветвях и напряжения на всех участках, составить баланс активных и реактивных мощностей, построить полную векторную диаграмму цепи, записать мгновенные значения токов, если u(t) = Um× sin(wt +yu); Um = 600 B; yu = -90°; r1 =10 Ом, r3 = x2 = x3 =20 Ом, x4 =20 Ом. Решение Заменим разветвлённый участок исходной схемы эквивалентной ветвью с параметрами r23, х23, для чего рассчитаем активные и реактивные (с учётом характера сопротивлений) проводимости параллельных ветвей: g2 = g3 = g23 = g2 + g3 = 0 + 0, 025 = 0, 025 Cм; b23 = |b2 – b3| = 0, 05 – 0, 025 = 0, 025 Cм (инд.); r23 = x23 = Эквивалентная схема, по которой рассчитаем ток в неразветвлённой части цепи, приведена на рис. 3.18, б: i1(t) = I1m× sin(wt +yu – j вх); где I1m = j вх = arctg Решение В рассматриваемой схеме два разветвления: на участке bc параллельно включены 2я и 3я ветви, которые могут быть заменены эквивалентной ветвью r23-x23 (рис. 3.20, б); на участке de параллельно включены 5я и 6я ветви, заменяемые последовательной эквивалентной цепью r56-x56. Замена осуществляется на основании соотношений между активными и реактивными проводимостями параллельных ветвей: g2 = g3 = 0; b3 = g23 = g2 + g3 = 0, 03 + 0 = 0, 03 Cм; b23 = b2 + b3 = 0, 01 + 0, 03 = 0, 04 Cм (инд.); r23 = x23 = g5 = 0; g6 = g56 = g5 + g6 = 0 + 0, 1 = 0, 1 Cм; b56 = b5 + b6 = 0, 05 + 0 = 0, 05 Cм (ёмк.); r56 = Входное сопротивление цепи по эквивалентной схеме (рис. 3.20, б) Zвх = = cosj вх = sinj вх = Ток в общей части схемы I1 = I4 = напряжения на разветвлениях Ubc = I1× Ude = I1× токи в остальных ветвях I2 = I3 = Проверим балансы мощностей. Баланс активных мощностей представляется для схемы рис. 3.20, а выражением U× I1× cosj вх = I12× r1 + I22× r2 + I62× r6, 300× 10× 0, 8 = 102× 4+ или 3000 Вт = 3000 Вт - выполняется. Баланс реактивных мощностей цепи U× I1× sinj вх = I12× x1 + I22× x2 + I32x3 – I42× x4 – I52× x5, 300× 10× 0, 6 = 102× 8 + или 1800 вар = 800 + 400 + 1200 – 200 – 400 вар - выполняется. Так как оба баланса мощностей выполняются, задача расчёта цепи решена верно, и можно переходить к построению векторной диаграммы. Так как в схеме рис. 3.20, а имеется два разветвления, то сначала строится векторная диаграмма для последовательной эквивалентной схемы рис. 3.20, б и построение начинается с выбора произвольного направления вектора тока I1 последовательной цепи (горизонтально, вправо) (рис. 3.21). Уравнение по второму закону Кирхгофа запишем в векторной форме с соблюдением принципа: падения напряжений на элементах схемы строго следуют в соответствии с расположением элементов, и каждому вектору напряжения присваиваются соответствующие индексы точек схемы: При этом I1× r23= 10× 12 = 120 B, I1× x23= 10× 16 = 160 B, Ucd = I1× x4= 10× 2 = 20 B, I1× r56= 10× 8 = 80 B, I1× x56= 10× 4 = 40 B, I1× r1= Uef = 10× 4 = 40 B. На рис. 3.21 падения векторных напряжений построены пунктирно, так как эти напряжения отсутствуют в исходной схеме. Далее переходим к построению векторов токов I2 и I3. Ток I3 перпендикулярен напряжению Ubc, а ток Параллельно вектору Ude откладывается ток I6, а ток
Затем относительно тока I2 откладываются векторы падений напряжений 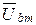 = = 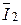 × x2 и × x2 и  = = 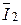 × r2. × r2.
Векторная диаграмма принимает окончательный вид рис. 3.21. На этой векторной диаграмме указан также вектор напряжения
U = 200 B; r1 = 30 Ом; x1 = 50 Ом; x2 = 10 Ом; r3 = 5 Ом; x3 = 15 Ом. Определить показания приборов. Решение 1. Заменяем параллельное соеди-нение ветвей 2 и 3 эквивалентным последовательным соединением сопротивлений r23 и x23: g2 = 0; b2 = g3 = g23 = g2 + g3 = 0 + 0, 02 = 0, 02 Cм; b23 = b2 – b3 = 0, 1 – 0, 06 = 0, 04 Cм; Y23 = r23 = 2. Входное сопротивление цепи и её коэффициент мощности: Z = |
Последнее изменение этой страницы: 2017-03-15; Просмотров: 4133; Нарушение авторского права страницы