В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке AB? в треугольнике ABC?

В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке AB? в треугольнике ABC?

Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( ), а в какое-то подмножество А . Вероятность Р(А) пропорциональна мере (длин, площади и т.д.) множества А, т.е. Р(А)= с (А) ), где (А)-мера множества А, а с=const. Т.к. P( )=1, то с = 1/ ( ), так что Р(А)= .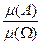

1) - АВ, F-отрезок СD, СD АВ. - длина, (CD)=d-c, (BA)=b-a, значит

Р(А)= . 2) -треугольник АВС, F-фигура . (F)=площадь F, ( )-площадь АВС. Р(F)=площадь F/ площадь ABC.

Схема Бернулли

30. В чем состоит схема Бернулли? Запишите формулу для вероятности успехов в серии испытаний по схеме Бернулли и приведите пример ее применения.

Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p наступает событие , противоположное А.

Пусть k – любое из чисел 0, 1, 2, …, n. Обозначим вероятность того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли:

.

Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?

Решение: В данном случае успехом считается выпадение герба, вероятность p этого события в каждом опыте равна ½ , так что q=1-p=1|2. Отсюда

.

 

33. Пусть – вероятность успехов в серии независимых испытаний с вероятностью успеха в каждом испытании. При каком 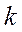вероятность 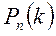достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов? Чему равна сумма ?

Рассмотрим два соседних числа и . М ежду ними имеет место одно из соотношений: ( меньше, равно или больше) или, что эквивалентно, . Подставляя вместо числителя и знаменателя их выражения по формулам , или учитывая, что , получим соотношения 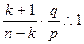или . Собирая все слагаемые с множителем k и учитывая, что p+q=1 , получим эквивалентные соотношения 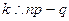. Обозначим число np+p через . Тогда перепишется: .

Таким образом, для всех значений k меньших чем справедливо неравенство , для ( это возможно только в том случае, когда - целое число) имеет место равенство 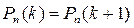, наконец, при выполняется неравенство . Тем самым при значениях функция возрастает, а при значениях убывает. Следовательно, если число не является целым, то функция имеет единственный максимум; он достигается при ближайшем к слева целом значении k , т.е. при таком целом 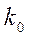, которое заключено между -1 и : np-q< 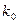< np+p, 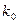=[np+p].

Если же - целое число, то два равных между собой максимума достигается при и .

Если число не является целым, то наиболее вероятное число успехов равно ближайшему к слева целому числу. В случае когда есть целое число, наиболее вероятное число успехов имеет два значения: -1 и . Сумму не знаю как посчитать.

 

Сформулируйте и докажите предельную теорему Пуассона.

При n®¥, p®0 b, а величина l = np остаётся постоянной .

Док-во: имеем: , и так как p=l/n, то . Выражение - это произведение k множителей, стремящихся к 1; поэтому и всё произведение стремится к 1. Выражение стремится к 1. Что касается выражения 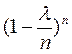, то его можно записать в виде . Замечая, что выражение в квадратных скобках имеет пределом число , получим окончательно: 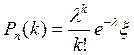, где x®1. Отсюда тотчас же следует формула, указанная в теореме.

40. Запишите приближенные формулы Пуассона. При каких условиях они дают хорошее приближение? Приведите пример их применения.

формулы Пуассона: и 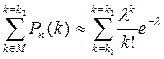. Они дают хорошее приближение при больших n и малых p (npq£ 10). Пример: в тесто засыпают большое количество изюма (например, 10000 изюмин) и нужно оценить вероятность того, что в случайно выбранной булке, испечённой из этого теста, окажется, к примеру, ровно 2 изюмины). То есть получается, что p=2/10000 = 0, 0002). В этом случае также npq< 10. В итоге, можем применять приближённую формулу Пуассона.

 

 

Может ли график функции распределения быть прямой линией? Ответ обоснуйте.

Нет, не может, т.к.

.Функция ступенчатая, со скачками в точках х1, х2.., причем величины качков равны соответственно р1, р2..

 

44. Что такое дискретная случайная величина? Может ли таблица

В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке AB? в треугольнике ABC?

Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( ), а в какое-то подмножество А . Вероятность Р(А) пропорциональна мере (длин, площади и т.д.) множества А, т.е. Р(А)= с (А) ), где (А)-мера множества А, а с=const. Т.к. P( )=1, то с = 1/ ( ), так что Р(А)= .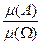

1) - АВ, F-отрезок СD, СD АВ. - длина, (CD)=d-c, (BA)=b-a, значит

Р(А)= . 2) -треугольник АВС, F-фигура . (F)=площадь F, ( )-площадь АВС. Р(F)=площадь F/ площадь ABC.

1234Следующая ⇒

Поделиться: