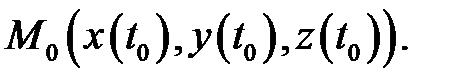Частные производные и дифференциалы высших порядков. Равенство смешанных производных

Если функции 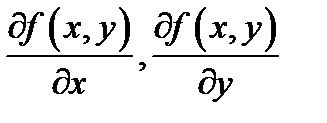дифференцируемы в точке 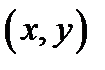и некоторой ее окрестности, то функции

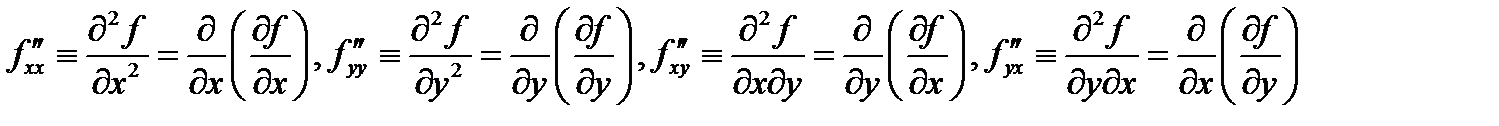
называются вторыми частными производными функции 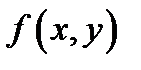в точке 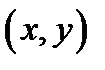(при этом производные 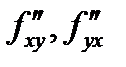называются смешанными производным). Аналогично определяются частные производные более высокого порядка. Например,

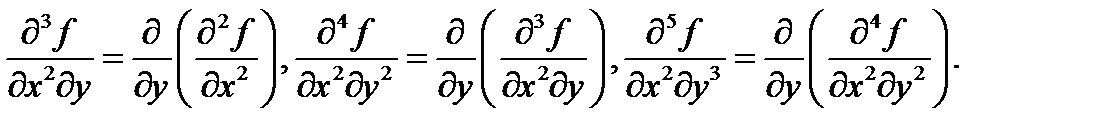
Если функция 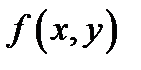непрерывна в точке 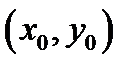и имеет в этой точке непрерывные частные производные до 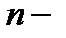порядка включительно, то её называют 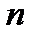раз дифференцируемой в этой точке.

Имеет место следующее утверждение.

Теорема 5 (о равенстве смешанных производных). Пусть в точке 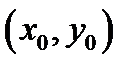и в некоторой ее окрестности существуют частные производные 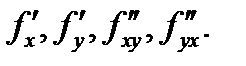Тогда если смешанные производные

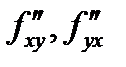непрерывны в точке 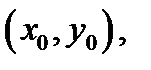то они совпадают в этой точке: 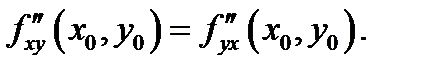Аналогичное утверждение имеет место и для смешанных производных более высокого порядка (например, 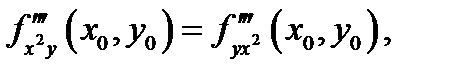если частные производные 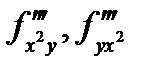непрерывны в точке ).

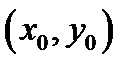Пример 1. Найти вторые смешанные производные для функции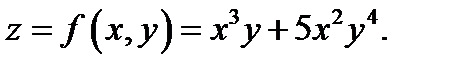

Решение. Имеем

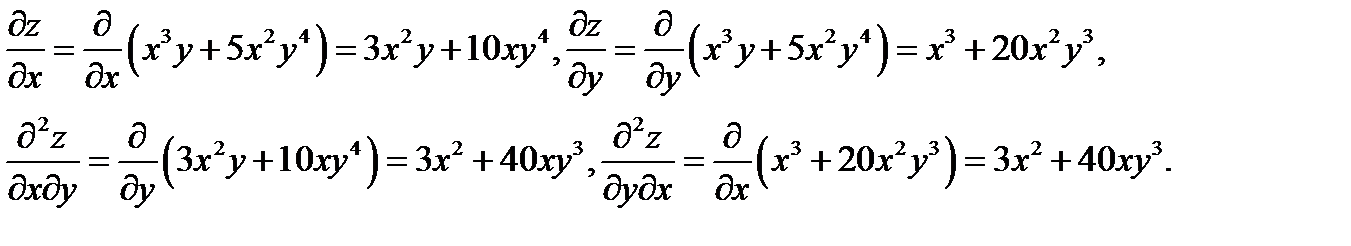
По аналогии с дифференциалами высших порядков функции одной переменной определяются и дифференциалы высших порядков для функций многих переменных. А именно, если известен дифференциал 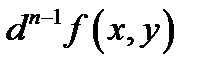порядка 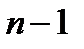, то дифференциал 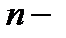го порядка определяется по индукции: 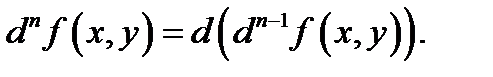При этом дифференциалы независимых переменных 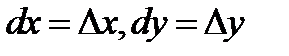и их степени 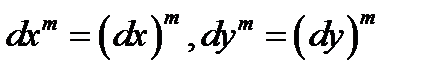считаются постоянными дифференцирования.

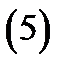Если функция 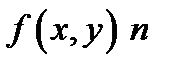раз дифференцируема в точке 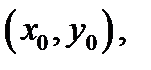то ее дифференциал 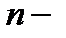порядка в этой точке вычисляется по формуле

 

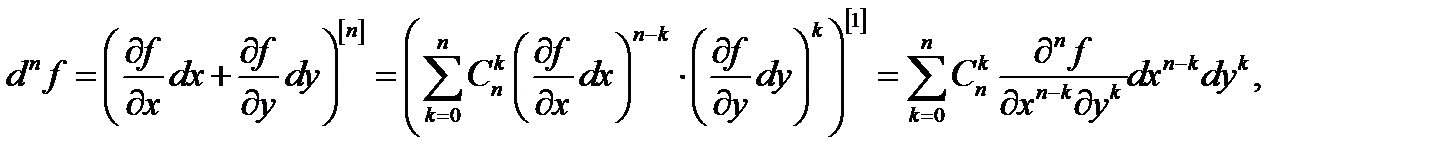
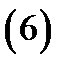
где 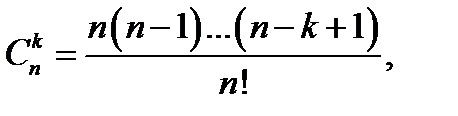символ 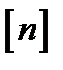означает, что надо сначала выражение 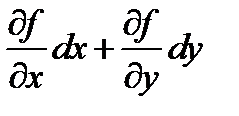возвести в 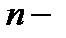ую степень [3], а затем произведения вида 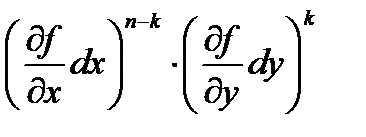заменить на частные производные 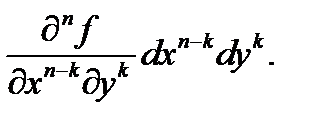Например,

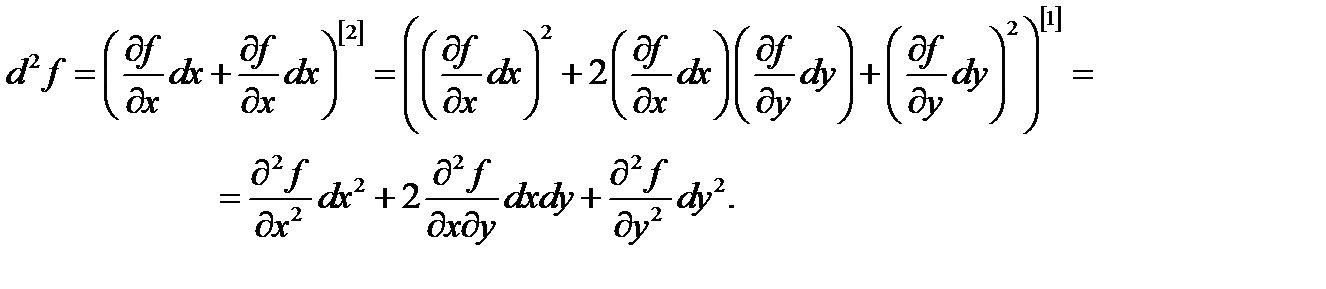
С помощью дифференциалов высших порядков можно в краткой форме записать формулу Тейлора для функций многих переменных.

Теорема 7. Пусть в точке 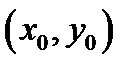и некоторой её окрестности 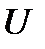функция 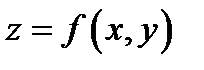имеет непрерывные частные производные до 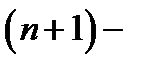порядка включительно. Тогда для каждой точки 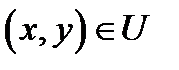имеет место представление

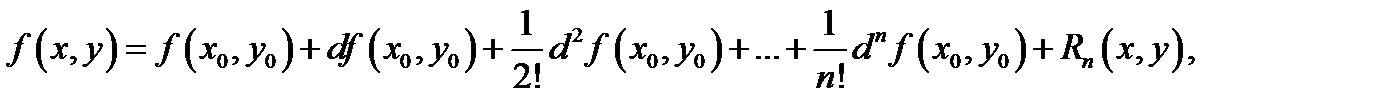
где 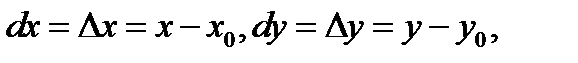остаточный член 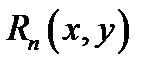(в форме Лагранжа) имеет вид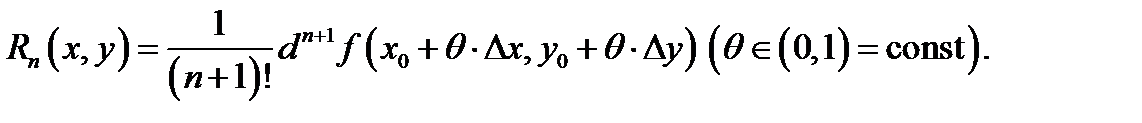

Скалярное поле. Производная скалярного поля по направлению, связь с градиентом

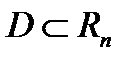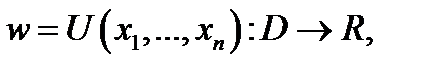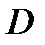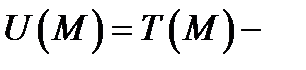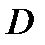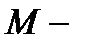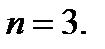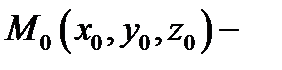Если в некоторой области задана функция то говорят, что в задано скалярное поле. Например, температура тела в точке является скалярным полем. Будем, как и прежде, рассматривать случай Пусть фиксированная точка области 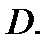Сместимся из точки 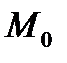в точку 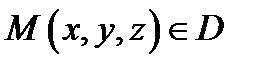по направлению 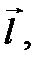определяемым единичным вектором 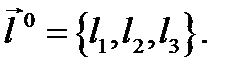Введем следующее понятие.

Определение 2. Если существует конечный предел

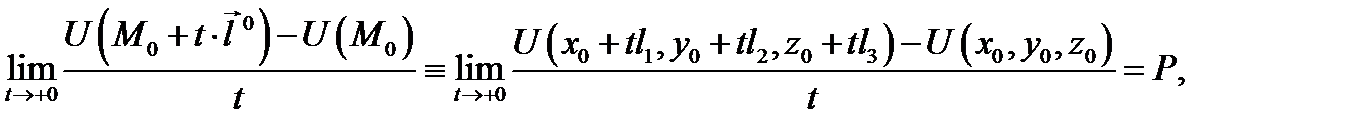
то его называют производной поля 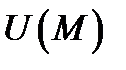в точке 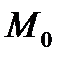по направлению 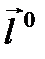и обозначают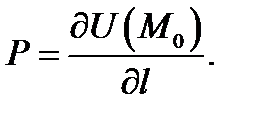

Производная 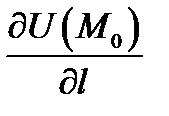показывает скорость изменения поля 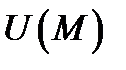в точке 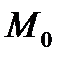в направлении 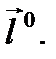Введем ещё одно понятие.

Определение 3. Градиентом скалярного поля 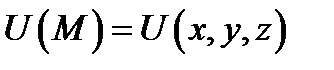в точке 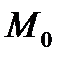называется вектор

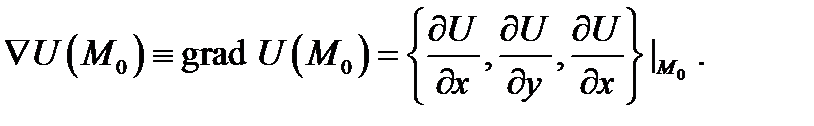
Следующая теорема устанавливает связь между градиентом и производной поля по направлению.

Теорема 8. Если поле 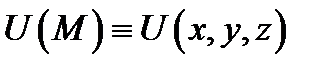дифференцируемо в точке 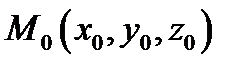и 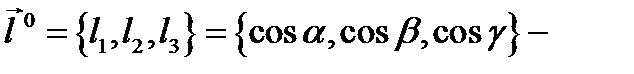единичный вектор направления 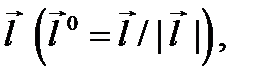то

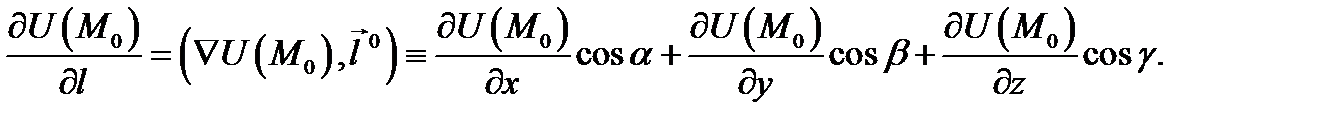
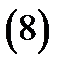
Доказательство проведем для плоского скалярного поля. Рассмотрим функцию 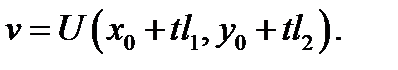По определению 2 имеем 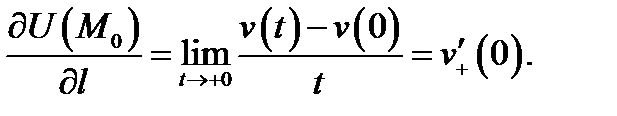Так как функция 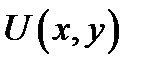дифференцируема в точке 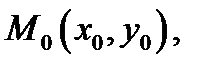а функции 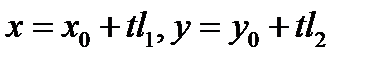дифференцируемы в точке 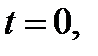то сложная функция 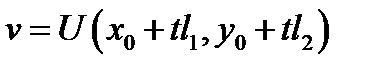дифференцируема в точке 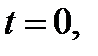причем

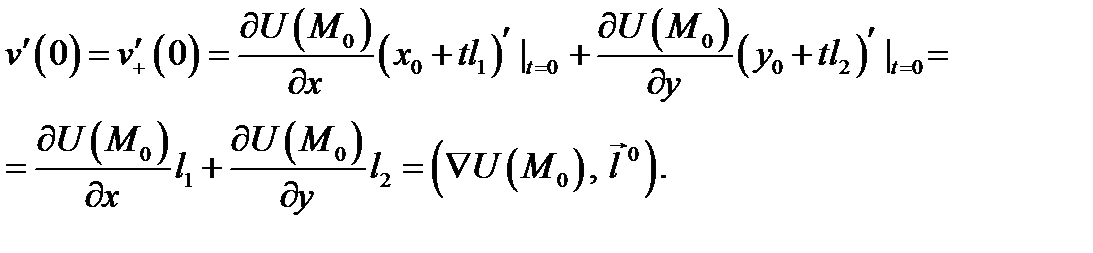
Теорема доказана.

Данное нами определение градиента зависит от выбора системы координат. Инвариантное определение градиента следующее: градиентом поля 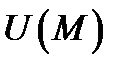в точке 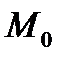называется такой вектор 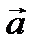, проекция которого на произвольное направление 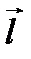в этой точке совпадает с производной поля 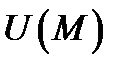по направлению 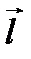в точк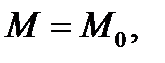е т.е.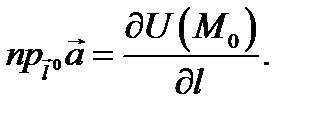

Если выбрать систему координат с ортами 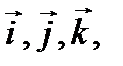то 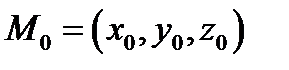и взять 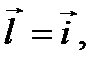то по теореме 8 получаем, что

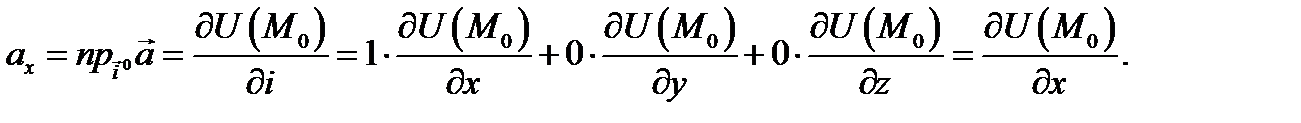
И аналогично, 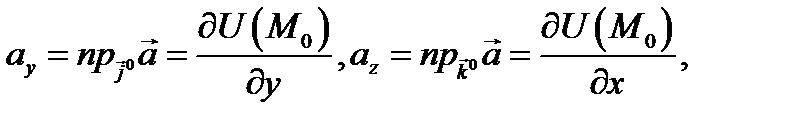и мы получаем ранее данное определение градиента: 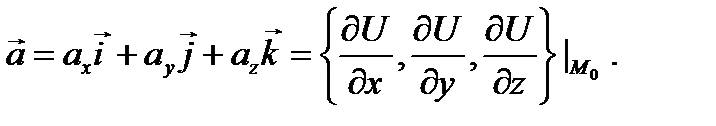Нетрудно установить следующие свойства градиента.

Производная по направлению 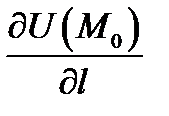имеет наибольшее значение в направлении

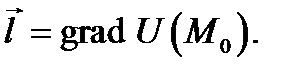При этом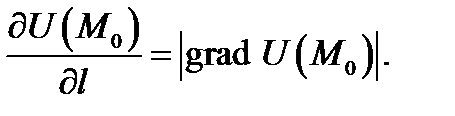

Градиент 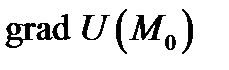направлен по нормали к поверхности уровня 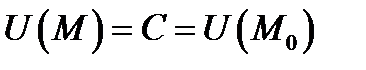в сторону наибольшего изменения поля 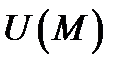в точке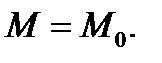

Лекция 3. Касательная плоскость и нормаль к поверхности. Локальный экстремум функции нескольких переменных, необходимое условие экстремума. Достаточные условия существования экстремума. Наибольшее и наименьшее значения функции на замкнутом ограниченном множестве. Условный экстремум и метод множителей Лагранжа

 

Прежде чем перейти к изложению следующего раздела, отметим, что кривую в пространстве 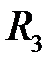можно задать системой уравнений

.

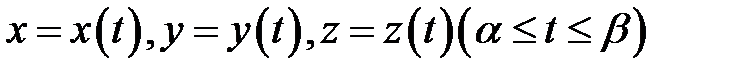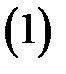
Действительно, при изменении параметра 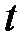на отрезке 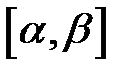точка 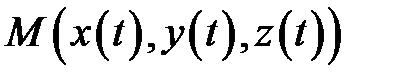описывает в 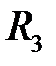некоторую кривую 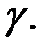При этом кривая 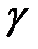называется непрерывной, если все функции непрерывны на отрезке 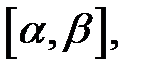и 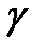называется гладкой кривой, если производные 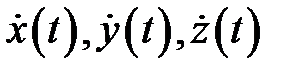непрерывны на указанном отрезке. Точка 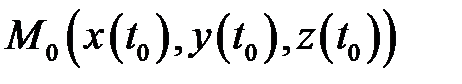называется неособой, если 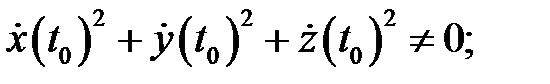в противном случае (т.е. в случае 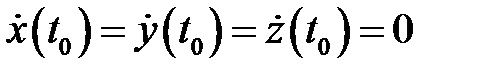)точка 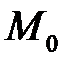называется особой. Нетрудно показать, что вектор 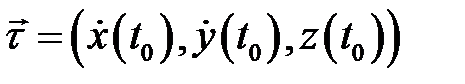является касательным вектором к кривой 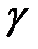в точке

⇐ Предыдущая123456789Следующая ⇒

Поделиться: