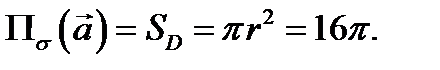Двойной интеграл в полярных координатах
Рассмотрим функции 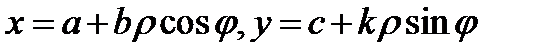
Эти функции будут взамно однозначно отображать плоскость переменных  на плоскость переменных
на плоскость переменных 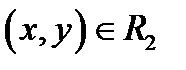 , если условиться, что точка
, если условиться, что точка 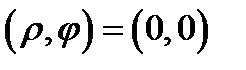 переходит только в точку
переходит только в точку 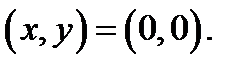 Криволинейные координаты
Криволинейные координаты 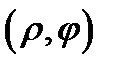 называют в этом случае обобщенными полярными координатами, а в случае
называют в этом случае обобщенными полярными координатами, а в случае 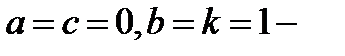 просто полярными координатами в плоскости
просто полярными координатами в плоскости  Вычислим якобиан перехода для таких координат. Имеем
Вычислим якобиан перехода для таких координат. Имеем

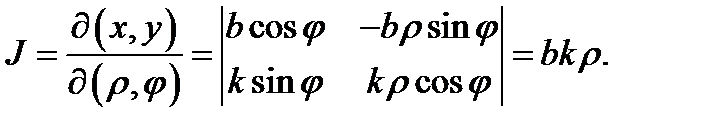
Из теоремы 1 вытекает, что двойной интеграл в обобщенных полярных координатах будет таким:

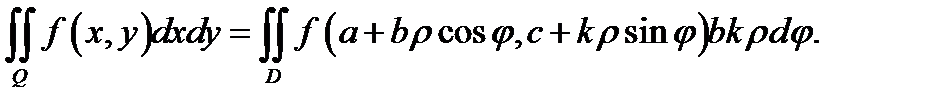
При 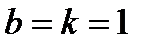 получаем формулу
получаем формулу
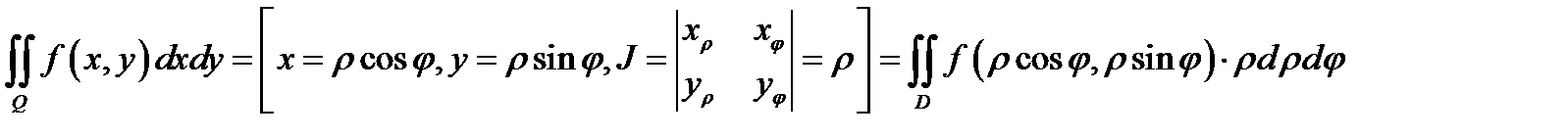
для двойного интеграла в полярных координатах. Здесь и выше 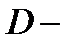 область, которая при отображении
область, которая при отображении 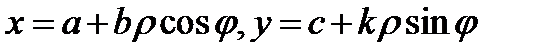 переходит в область
переходит в область 
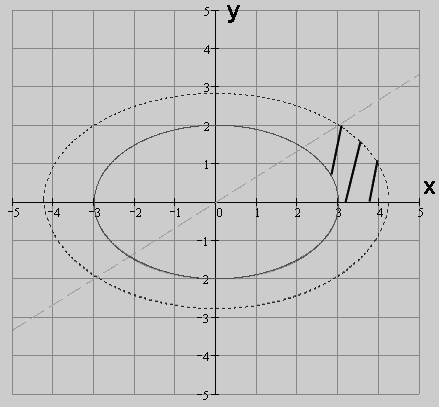
Пример 1 ( ( Кузнецов Л.А. Типовые расчеты ). Пластинка  задана неравенствами
задана неравенствами 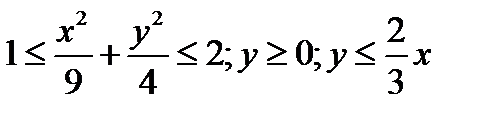 ,
, 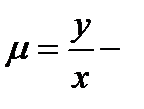 поверхностная плотность. Найти массу пластинки.
поверхностная плотность. Найти массу пластинки.
 Решение. Введем обобщенные полярные координаты
Решение. Введем обобщенные полярные координаты
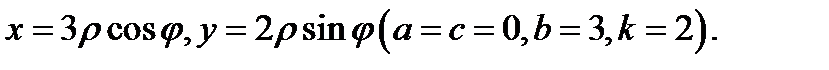
При этом эллипсы 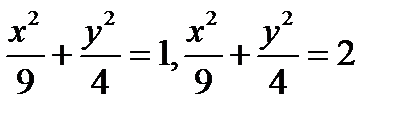 перейдут в прямые
перейдут в прямые 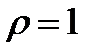 и
и 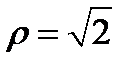 соответственно, а прямая
соответственно, а прямая 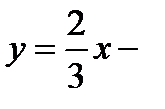 в луч
в луч 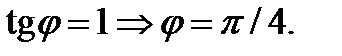 Якобиан перехода будет таким:
Якобиан перехода будет таким: 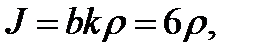 поэтому
поэтому
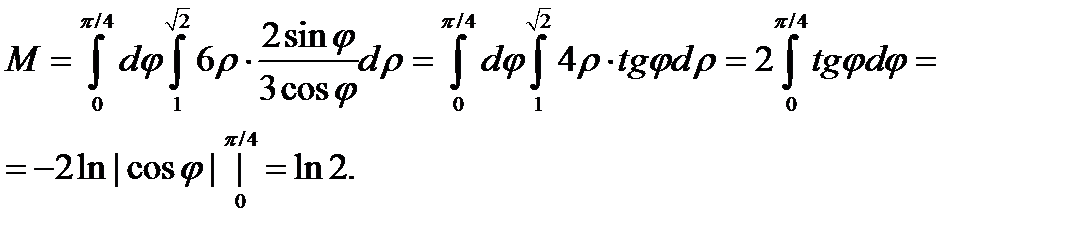
Криволинейные координаты в пространстве. Тройной интеграл в цилиндрических и сферических координатах
Криволинейные координаты в пространстве вводятся аналогично. Если  область переменных
область переменных  , заданных в прямоугольных декартовых координатах, то упорядочная тройка чисел
, заданных в прямоугольных декартовых координатах, то упорядочная тройка чисел 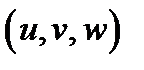 , связанная с предыдущей тройкой равенствами
, связанная с предыдущей тройкой равенствами
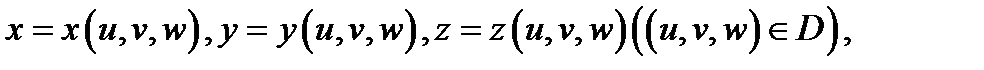
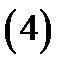
осуществляющими взаимно однозначное отображение области 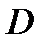 на область
на область 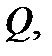 называется
называется
криволинейными координатами точки 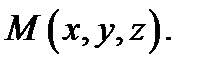 При этом поверхности
При этом поверхности
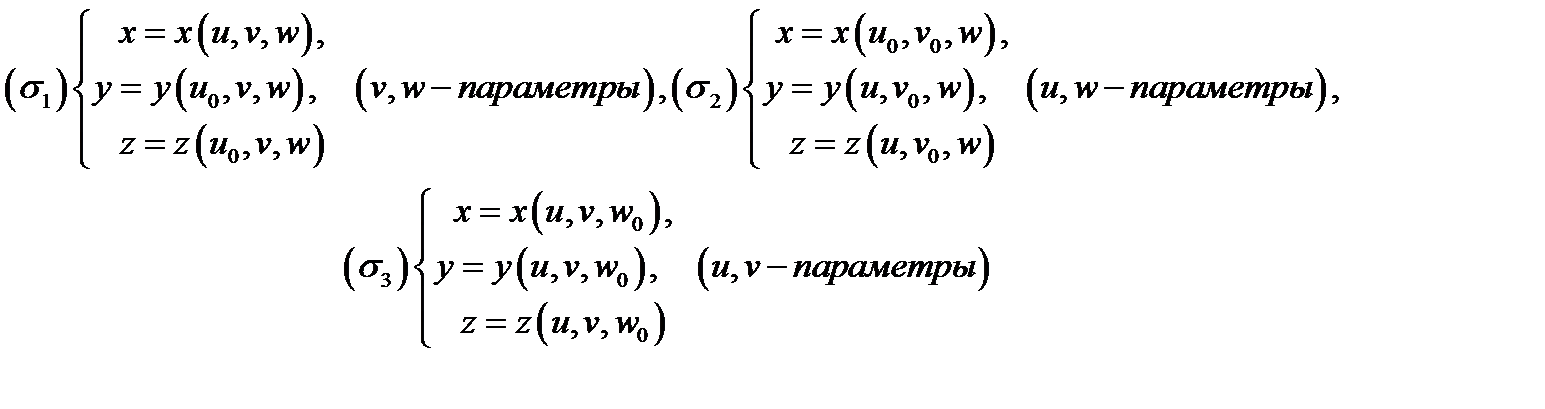
называются координатными поверхностями точки 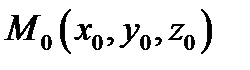 (пересечением именно этих поверхностей является точка
(пересечением именно этих поверхностей является точка 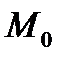 ). Определитель
). Определитель
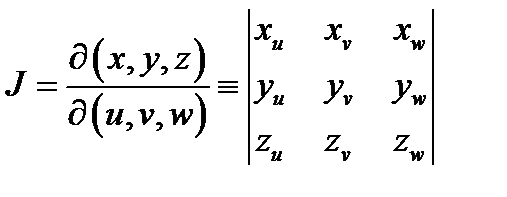
называется якобианом отображения (4) или якобианом перехода от декартовых координат к криволинейным. Его геометрический смысл состоит в следующем: 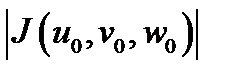 есть коэффициент искажения объёма малого параллелепипеда с вершиной в точке
есть коэффициент искажения объёма малого параллелепипеда с вершиной в точке 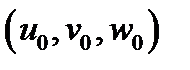 и рёбрами
и рёбрами 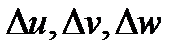 при отображении (4), т.е.
при отображении (4), т.е. 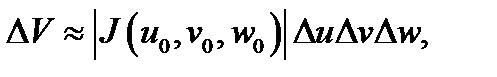 где
где 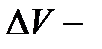 объём образа указанного параллелепипеда при отображении (4). Используя этот факт, нетрудно доказать следующее утверждение.
объём образа указанного параллелепипеда при отображении (4). Используя этот факт, нетрудно доказать следующее утверждение.
Теорема 2. Имеет место равенство
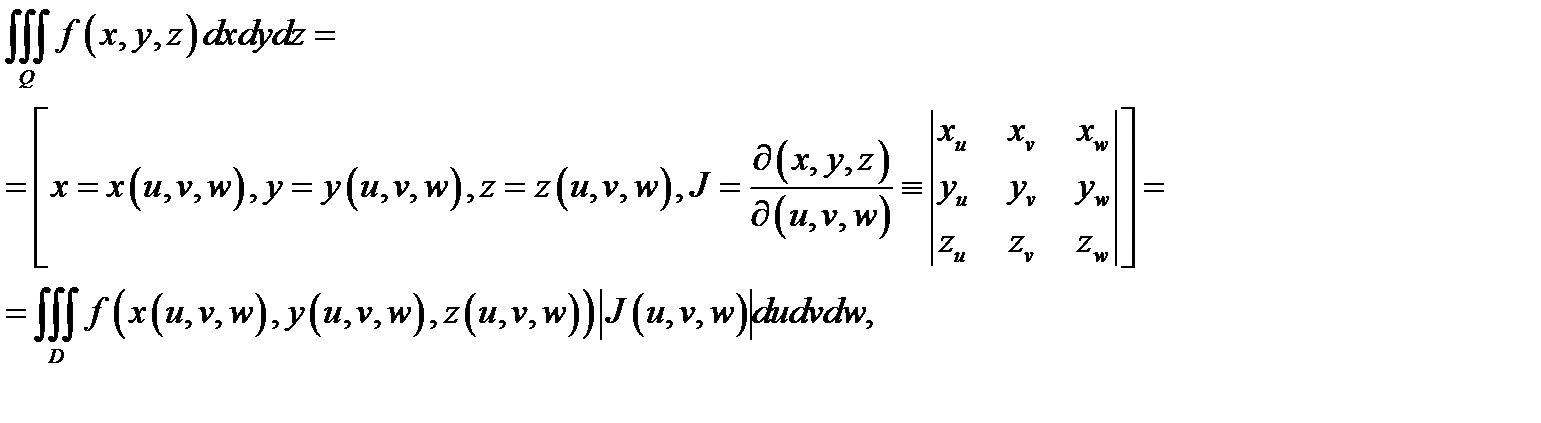
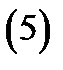
если выполняются следующие условия:
1) функция 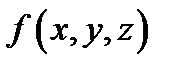 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 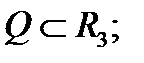
2) функции 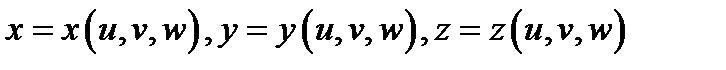 непрерывно дифференцируемы в области
непрерывно дифференцируемы в области 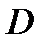 и взаимно однозначно отображают область
и взаимно однозначно отображают область 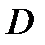 на область
на область 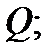
3) 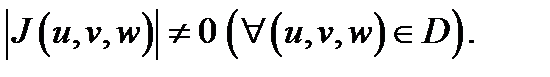
Цилиндрическими координатами называются координаты 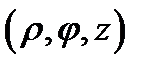 точки
точки 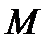 , связанные с декартовыми координатами
, связанные с декартовыми координатами 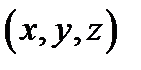 этой точки равенствами (см. Р.18)
этой точки равенствами (см. Р.18)
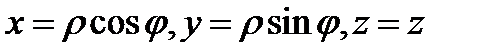
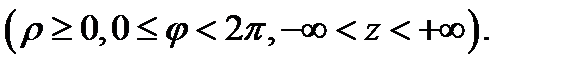
Нетрудно подсчитать, что якобиан перехода от декартовых координат к цилиндрическим будет равен 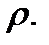 Действительно, имеем
Действительно, имеем
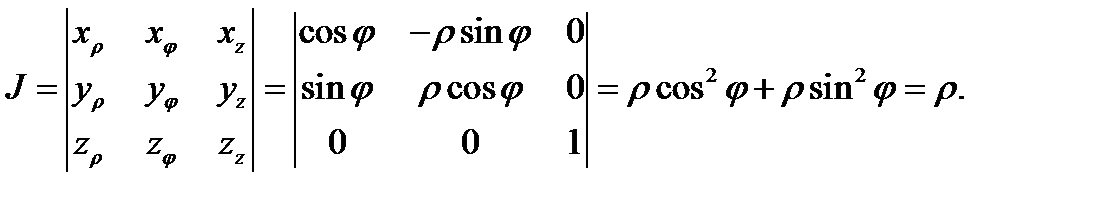
Следовательно, тройной интеграл в цилиндрических координатах запишется так (см. (5)):
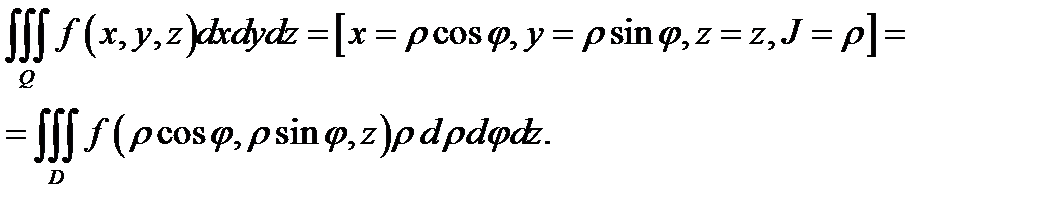
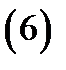
 Здесь
Здесь 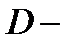 область, которая при отображении
область, которая при отображении 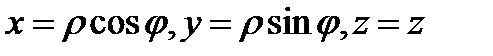 переходит в область
переходит в область 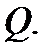
Сферическими координатами называются координаты 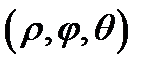 точки
точки 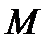 , связанные с декартовыми координатами
, связанные с декартовыми координатами 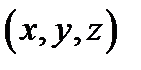 этой точки равенствами (см. Р.19)
этой точки равенствами (см. Р.19)
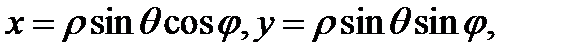
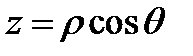
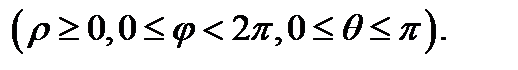
Нетрудно показать, что якобиан перехода от декартовых координат к сферическим равен
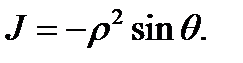 Используя теорему 2, запишем тройной интеграл в сферических координатах в виде
Используя теорему 2, запишем тройной интеграл в сферических координатах в виде
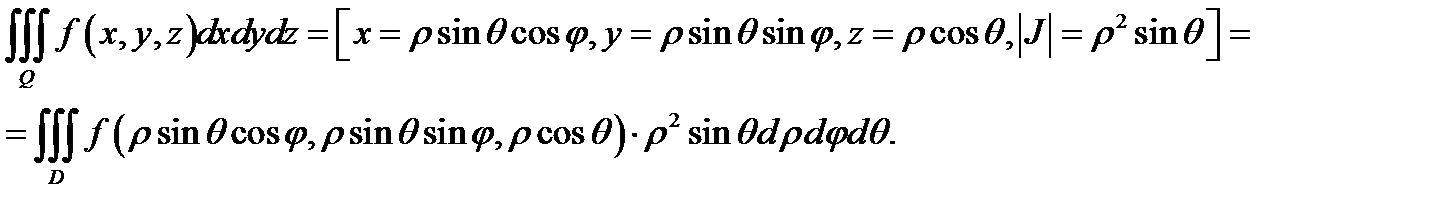
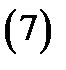
Здесь 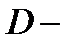 область, которая при отображении
область, которая при отображении 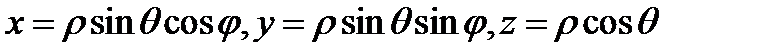 переходит в область
переходит в область 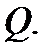
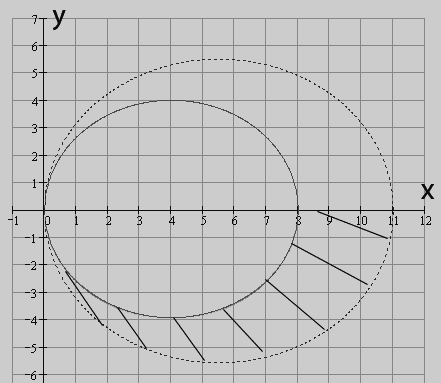
Пример 2 ( Кузнецов Л.А. Типовые расчеты ). Найти объем тела, заданного ограничиваю-
щими его поверхностями:
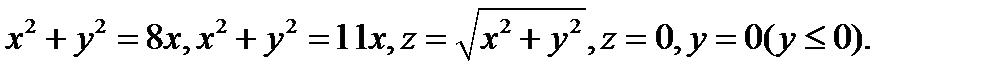
Решение. Объём тела будем вычислять с помощью тройного интеграла 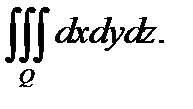 Введём цилиндрические координаты:
Введём цилиндрические координаты: 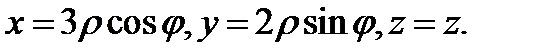 Тогда область
Тогда область 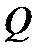 перейдёт в область
перейдёт в область 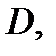 граница которой будет задаваться уравнениями
граница которой будет задаваться уравнениями 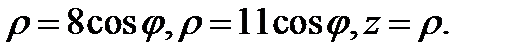 Граница проекции
Граница проекции  тела
тела 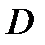 на плоскость
на плоскость 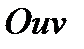 будет такой
будет такой 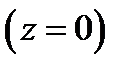 :
: 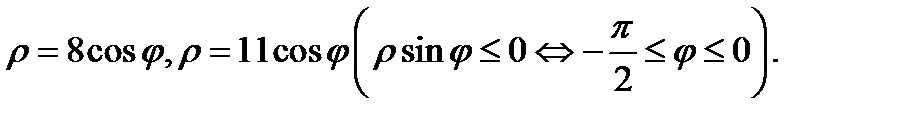 Луч с произвольным углом
Луч с произвольным углом 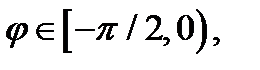 выходящий из начала
выходящий из начала 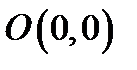 пересекает эту границу сначала в точке
пересекает эту границу сначала в точке 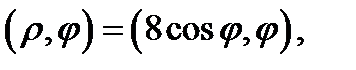 а затем – в точке
а затем – в точке 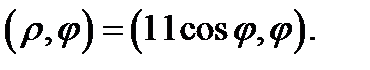 Значит, нижний и верхний пределы по
Значит, нижний и верхний пределы по  в повторном интеграле будут соответственно
в повторном интеграле будут соответственно  и
и 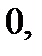 а пределы по
а пределы по 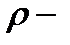 соответственно
соответственно 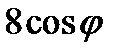 и
и 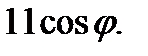 Взяв произвольно точку
Взяв произвольно точку 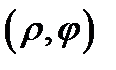 в проекции
в проекции 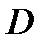 на плоскость
на плоскость 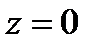 , выпустим из неё луч в направлении оси
, выпустим из неё луч в направлении оси 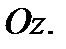 Он сначала пересечёт нижнюю границу области
Он сначала пересечёт нижнюю границу области 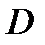 в точке
в точке 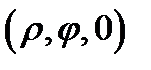 , а затем верхнюю границу области
, а затем верхнюю границу области 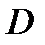 в точке
в точке 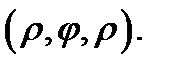 Значит, пределы по
Значит, пределы по 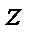 в повторном интеграле будут соответственно
в повторном интеграле будут соответственно 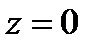 и
и 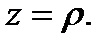 В результате будем иметь
В результате будем иметь
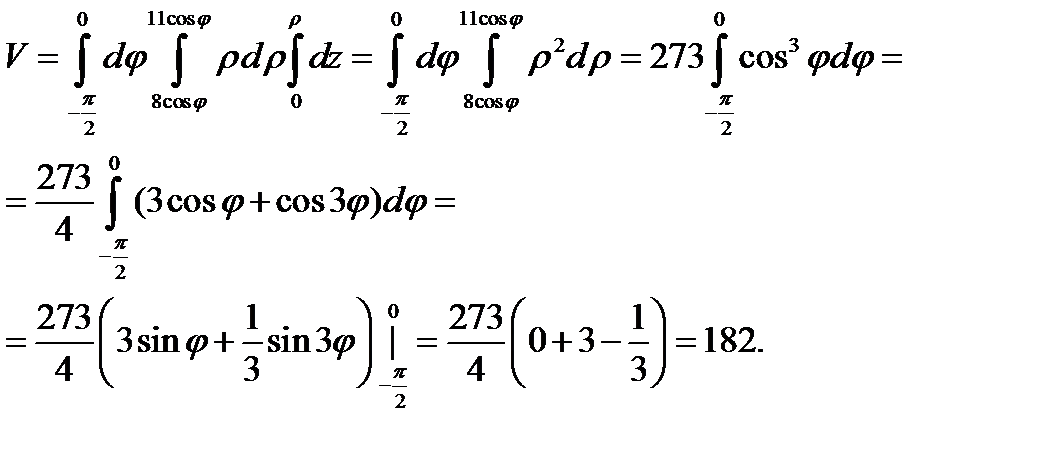
Площадь поверхности

Пусть в пространстве 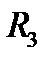 задана некоторая гладкая поверхность
задана некоторая гладкая поверхность  и пусть
и пусть 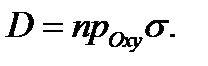 Произведем разбиение
Произведем разбиение
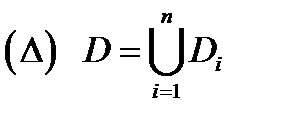 области
области 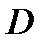 на частичные подобласти
на частичные подобласти 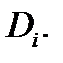 Это разбиение индуцирует разбиение
Это разбиение индуцирует разбиение 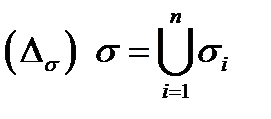 поверхности
поверхности  на частичные поверхности
на частичные поверхности 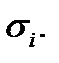 Возьмем произвольно точку
Возьмем произвольно точку 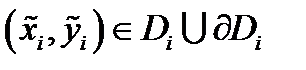 и в соответствующей точке
и в соответствующей точке 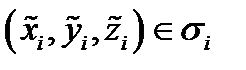 построим плоскость
построим плоскость 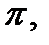 касательную к поверхности
касательную к поверхности 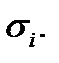 Цилиндр с основанием
Цилиндр с основанием 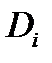 и образующей, параллельной оси
и образующей, параллельной оси 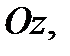 вырежит из этой плоскости кусок
вырежит из этой плоскости кусок 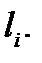 Обозначим через
Обозначим через 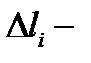 площадь куска
площадь куска 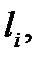 а через
а через 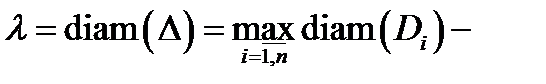 диаметр разбиения
диаметр разбиения 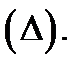
Определение 4. Если существует конечный предел 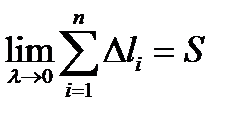 и он не зависит от вида разбиения
и он не зависит от вида разбиения 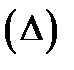 и выбора точек
и выбора точек 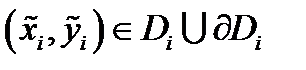 , то его называют площадью поверхности
, то его называют площадью поверхности 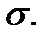
Теорема 3. Пусть поверхность  задаётся уравнением
задаётся уравнением 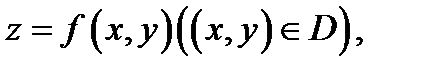 причем функция
причем функция 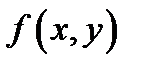 и её частные производные
и её частные производные 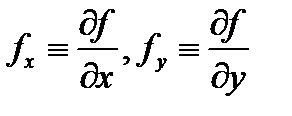 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области 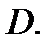 Тогда площадь поверхности
Тогда площадь поверхности  вычисляется по формуле
вычисляется по формуле
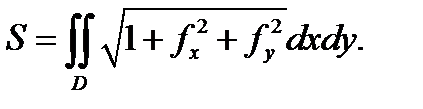
Доказательство. Вычислим площадь 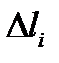 куска
куска 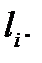 Так как
Так как 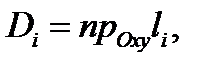 то
то 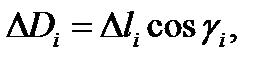
где 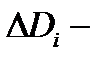 площадь области
площадь области 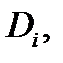 а
а 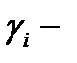 угол между плоскостями
угол между плоскостями 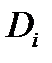 и
и 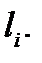 Угол
Угол 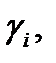 очевидно, равен углу между нормалями
очевидно, равен углу между нормалями 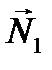 и
и 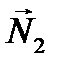 плоскостей
плоскостей 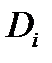 и
и 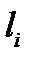 соответсвенно. Так как
соответсвенно. Так как 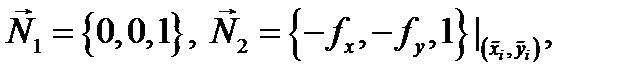 то
то
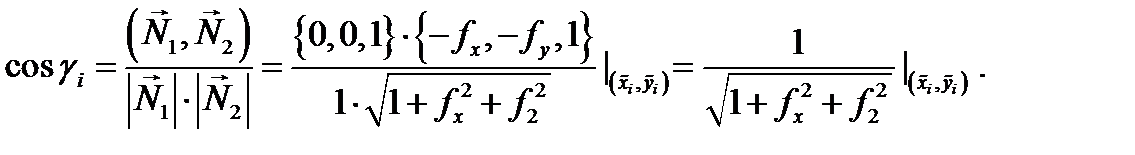
Следовательно, 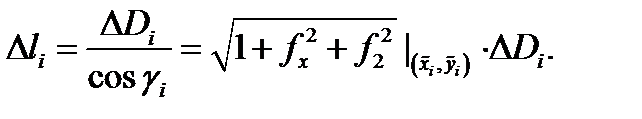 По определению 4 имеем
По определению 4 имеем
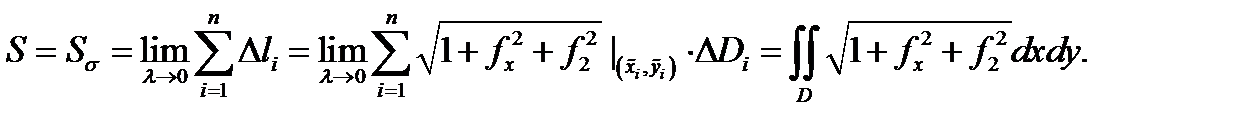
Теорема доказана.
Пример 3. Вычислить площадь части поверхности параболоида 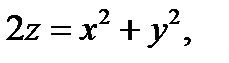 вырезан-
вырезан-
ную цилиндром 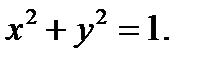
Решение. Здесь область 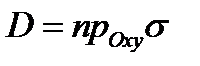 есть круг
есть круг 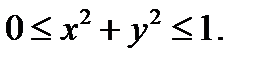 Площадь искомой поверхнос-
Площадь искомой поверхнос-
ти  находим по формуле (8):
находим по формуле (8):
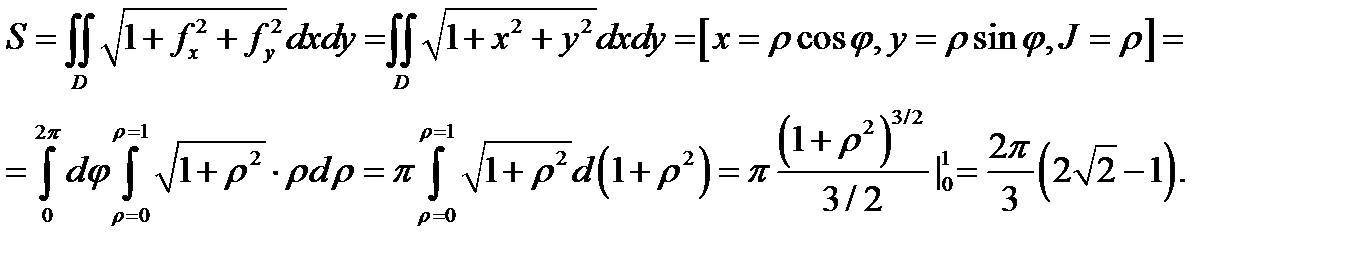
Лекция 6. Поверхностный интеграл первого рода (по площади поверхности) и его вычисление. Векторное поле. Векторные линии векторные трубки. Поток векторного поля, его свойства и вычисление. Дивергенция, её физический смысл и свойства. Формула Остроградского-Гаусса
Поверхностный интеграл
 Пусть в пространстве переменных
Пусть в пространстве переменных 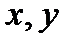 и
и 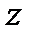 задана некоторая поверхность
задана некоторая поверхность  и пусть функция
и пусть функция 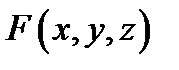 определена на этой поверхности. Произведём разбиение
определена на этой поверхности. Произведём разбиение 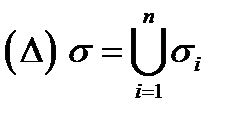 поверхности
поверхности  на частичные поверхности
на частичные поверхности 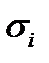 с помощью конечного числа непрерывных кривых. Возьмём произвольно точки
с помощью конечного числа непрерывных кривых. Возьмём произвольно точки 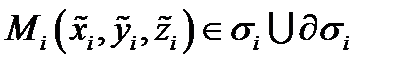 и составим интегральную сумму
и составим интегральную сумму 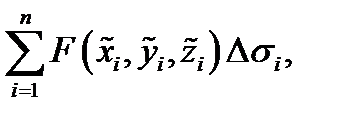 где
где 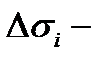 площадь куска
площадь куска 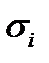 . Обозначим
. Обозначим 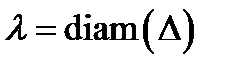 .
.
Определение 1. Если существует предел интегральных сумм: 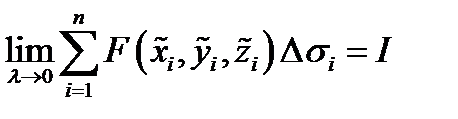 и если этот предел не зависит от вида разбиения
и если этот предел не зависит от вида разбиения 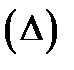 и выбора точек
и выбора точек 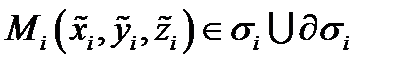 , то его называют поверхностным интегралом первого рода от функции
, то его называют поверхностным интегралом первого рода от функции 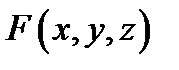 по поверхности
по поверхности  и обозначают
и обозначают 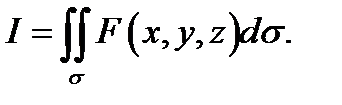
Теорема 1. Если поверхность  задана уравнением
задана уравнением 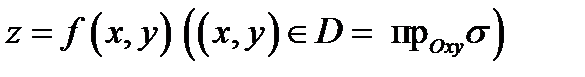 и функции
и функции
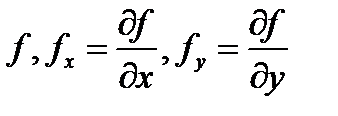 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области 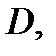 а функция
а функция 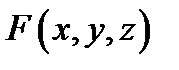 непрерывна на поверхности
непрерывна на поверхности 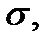 то
то
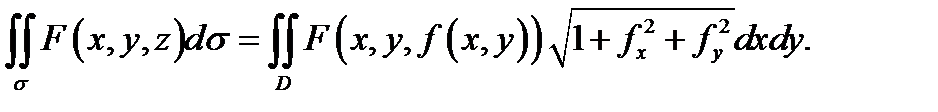
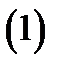
Доказательство следует из равенства
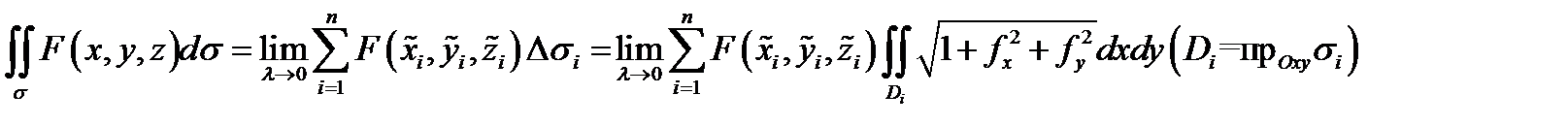
и теоремы о среднем 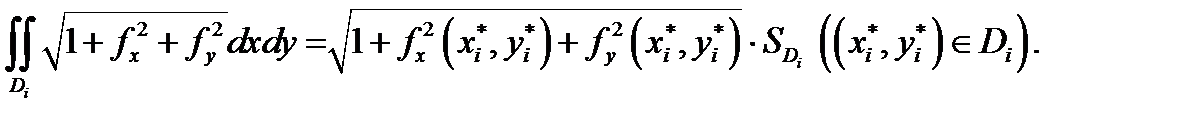 Подставляя это в предыдущее равенство и учитывая непрерывность всех функций, будем иметь
Подставляя это в предыдущее равенство и учитывая непрерывность всех функций, будем иметь
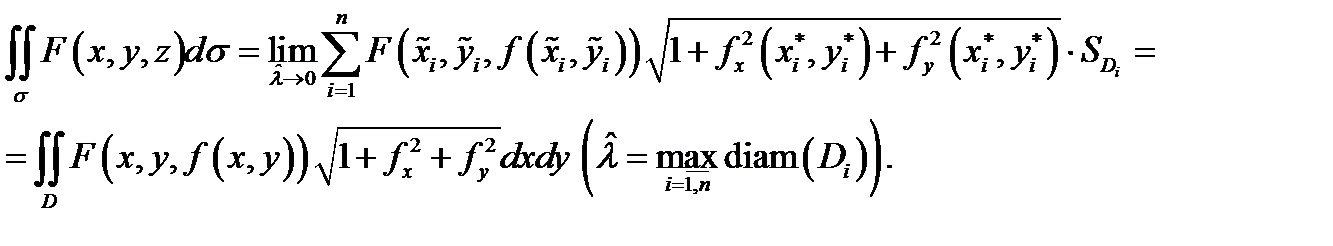
Теорема доказана.
Так как поверхностный интеграл сводится к двойному, то для него справедливы все свойства последнего: линейность, аддитивность, монотонность, теорема о среднем и т.д. Мы не будем их выписывать. Механический смысл поверхностного интеграла состоит в следующем: если 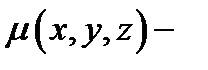 плотность пластинки
плотность пластинки  в точке
в точке 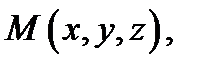 то
то 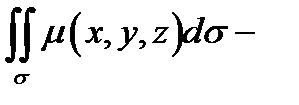 масса этой пластинки.
масса этой пластинки.
2. Векторное поле. Векторные линии векторные трубки. Ориентируемые поверхности и поток векторного поля через поверхность
Пусть 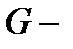 некоторая область в пространстве
некоторая область в пространстве 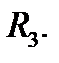
Определение 2. Говорят, что в области 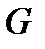 задано векторное поле
задано векторное поле 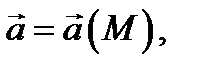 если в каждой точке
если в каждой точке 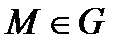 определен вектор
определен вектор 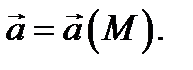
Это определение не зависит от выбора системы координат в 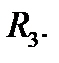 Если в
Если в 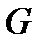 выбрана декартова система координат, то каждой точке
выбрана декартова система координат, то каждой точке 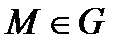 ставится в соответствие вектор
ставится в соответствие вектор
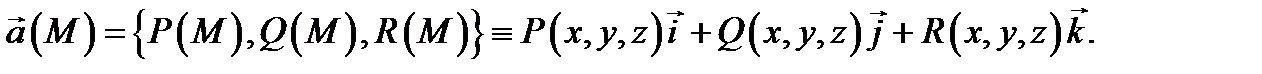
Примеры векторных полей: а)  скорость движущейся жидкости в точке
скорость движущейся жидкости в точке  (векторное полей скоростей жидкости); б)
(векторное полей скоростей жидкости); б) 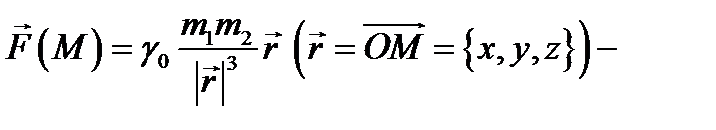 гравитационное поле (здесь тело массой
гравитационное поле (здесь тело массой 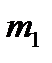 находится в точке
находится в точке 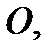 а тело массой
а тело массой 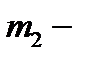 в точке
в точке 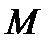 ,
, 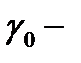 гравитационная постоянная).
гравитационная постоянная).
Векторное поле 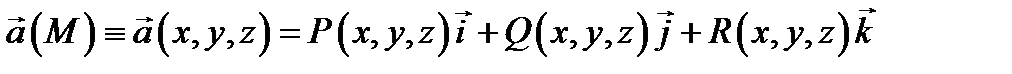 называеется непрерывным (кусочно непрерывным, гладким, непрерывно дифференцируемым) в области
называеется непрерывным (кусочно непрерывным, гладким, непрерывно дифференцируемым) в области 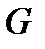 , если все его компоненты
, если все его компоненты 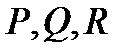 непрерывны (соответственно: кусочно непрерывны, гладки, непрерывно дифференцируемы) в области
непрерывны (соответственно: кусочно непрерывны, гладки, непрерывно дифференцируемы) в области 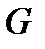 .
.
Пусть векторное поле 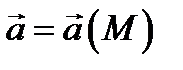 определено в области
определено в области 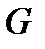 .
.
Определение 3. Линия 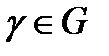 называется векторной линией поля
называется векторной линией поля 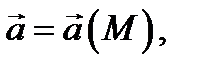 если в каждой точке
если в каждой точке 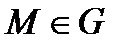 поле
поле 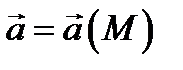 касается кривой
касается кривой 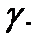 Поверхность
Поверхность 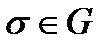 называется векторной трубкой поля
называется векторной трубкой поля 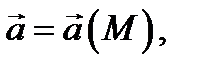 если она сплошь состоит из векторных линий этого поля.
если она сплошь состоит из векторных линий этого поля.
Теорема 2. Пусть поле 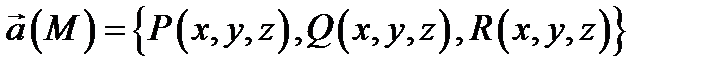 непрерывно дифференци-
непрерывно дифференци-
руемо в области 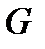 . Если
. Если 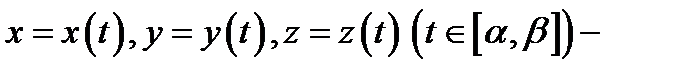 параметрические уравнения векторной линии поля
параметрические уравнения векторной линии поля 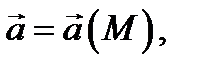 то для всех
то для всех 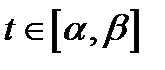 выполняются равенства
выполняются равенства
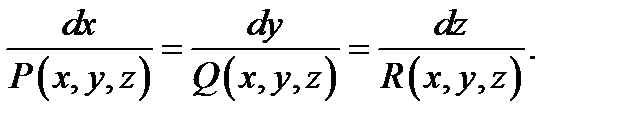
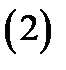
Обратно: если кривая 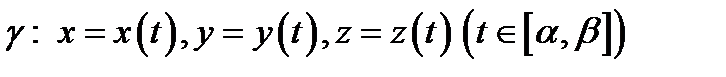 удовлетворяет соотношени-
удовлетворяет соотношени-
ям (1), то 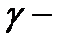 векторная линия поля
векторная линия поля 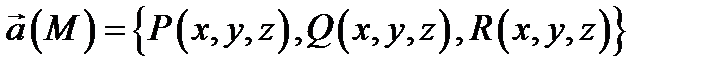 (уравнения (2) называются уравнениями векторных линий поля
(уравнения (2) называются уравнениями векторных линий поля 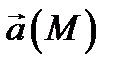 ).
).
Действительно, равенства (2) (если в них подставить уравнения 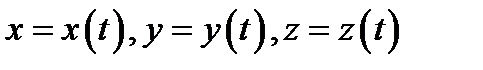
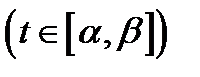 линии
линии 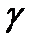 ) выражают условия коллинеарности векторов
) выражают условия коллинеарности векторов 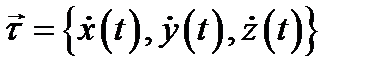 и
и 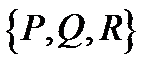 в одной и той же точке
в одной и той же точке 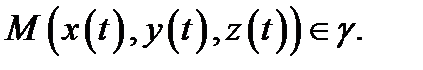 Значит, линия
Значит, линия 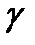 касается поля
касается поля 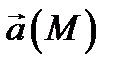 .
.
 Пусть в пространстве задана некоторая поверхность
Пусть в пространстве задана некоторая поверхность  и пусть в каждой точке
и пусть в каждой точке 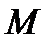 этой поверхности существует нормаль. На этой нормали можно выбрать два единичных вектора:
этой поверхности существует нормаль. На этой нормали можно выбрать два единичных вектора: 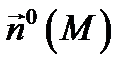 и
и 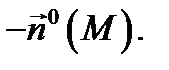
Определение 4. Если при движении точки  по любому замкнутому контуру, лежащему на поверхности
по любому замкнутому контуру, лежащему на поверхности  и не пересекающему её границы
и не пересекающему её границы  , единичный вектор
, единичный вектор  непрерывно изменяется и возвращается в точку
непрерывно изменяется и возвращается в точку  с первоначальным направлением, то говорят, что поверхность
с первоначальным направлением, то говорят, что поверхность  яв-
яв-
ляется двухсторонней. При этом сторона поверхности, определяемая вектором 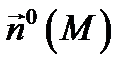 , называется внешней (или верхней) стороной поверхности
, называется внешней (или верхней) стороной поверхности  (обозначение:
(обозначение: 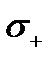 ), а сторона поверхности, определяемая вектором
), а сторона поверхности, определяемая вектором 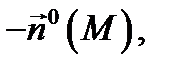 называется внутренней (или нижней) стороной поверхности
называется внутренней (или нижней) стороной поверхности  (обозначение:
(обозначение: 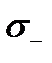 ). Векторы
). Векторы 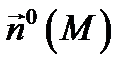 и
и 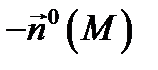 называются ориентациями поверхности
называются ориентациями поверхности  , а сама поверхность
, а сама поверхность  называется ориентируемой поверхностью.
называется ориентируемой поверхностью.
Если же на поверхности  найдётся хотя бы один замкнутый контур, при движении на котором единичный вектор
найдётся хотя бы один замкнутый контур, при движении на котором единичный вектор 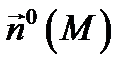 возвращается в точку
возвращается в точку 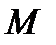 с противоположным направлением, то говорят, что поверхность
с противоположным направлением, то говорят, что поверхность  является односторонней или неориентируемой
является односторонней или неориентируемой
поверхностью.
Примером неориентируемой поверхности является лист Мёбиуса, который получается из прямоугольной полоски склеванием ее боковых после однократного их перекручивания. Перейдем к понятию потока векторного поля. Пусть дана двухсторонняя поверхность  и выбрана та её сторона, которая ориентирована единичной нормалью
и выбрана та её сторона, которая ориентирована единичной нормалью 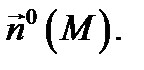
Определение 4. Потоком векторного поля 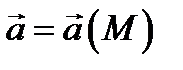 через поверхность
через поверхность  с ориентацией
с ориентацией 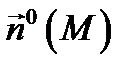 называется поверхностный интеграл
называется поверхностный интеграл
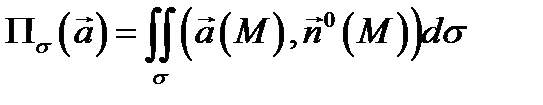
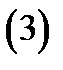
(здесь 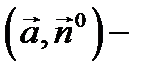 скалярное произведение векторов
скалярное произведение векторов 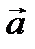 и
и 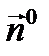 ).
).
Это определение потока не зависит от выбора системы координат. Если выбрана прямоугольная система координат, то
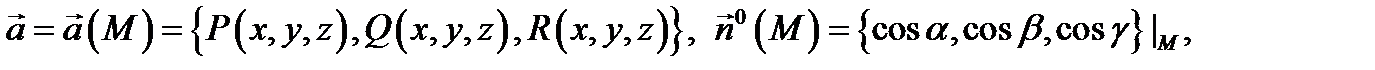
и поток можно записать в виде 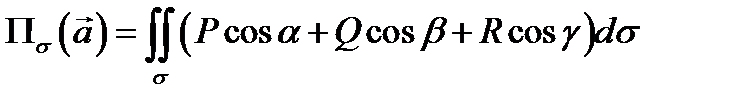 . Обозначив
. Обозначив
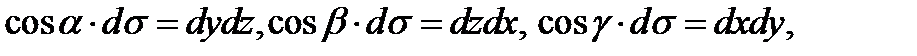 перепишем предыдущее равенство в виде
перепишем предыдущее равенство в виде
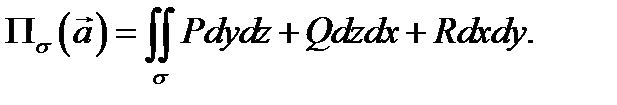 В таком виде поток записан в форме поверхностного интеграла второго рода (по координатам). Все три формы записи потока встречаются в математической литературе. Мы будем пользоваться первой формой записи, указанной в определении 4.
В таком виде поток записан в форме поверхностного интеграла второго рода (по координатам). Все три формы записи потока встречаются в математической литературе. Мы будем пользоваться первой формой записи, указанной в определении 4.
Из свойств поверхностного интеграла первого рода вытекают аналогичные свойства потока как поверхностного интеграла второго рода (линейность, аддитивность и т.д). Единственным отличием этих свойствах является то, что интеграл первого рода не зависит от ориентации поверхности 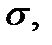 а интеграл второго рода (поток) зависит от выбора стороны поверхности:
а интеграл второго рода (поток) зависит от выбора стороны поверхности: 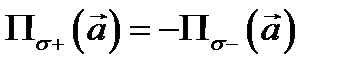 (это вытекает из определения 4). Дадим формулу вычисления потока.
(это вытекает из определения 4). Дадим формулу вычисления потока.
Теорема 3. Пусть 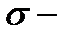 поверхность, задаваемая уравнением
поверхность, задаваемая уравнением 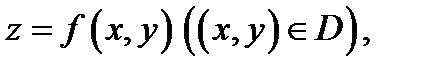 причем эта поверхность является гладкой, т.е. функции
причем эта поверхность является гладкой, т.е. функции 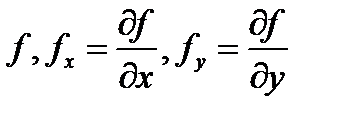 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области  Пусть, кроме того, векторное поле
Пусть, кроме того, векторное поле 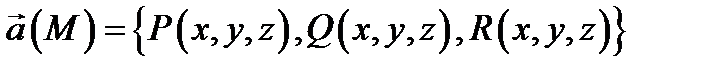 непрерывно на поверхности
непрерывно на поверхности  Тогда
Тогда

где знак (+) отвечает ориентации поверхности  нормальным вектором
нормальным вектором 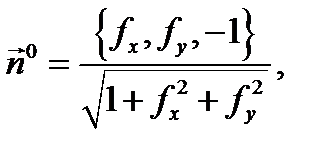 а знак (–) отвечает ориентации поверхности
а знак (–) отвечает ориентации поверхности  нормальным вектором
нормальным вектором 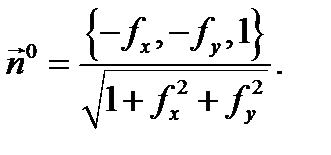
Доказательство. Пусть поверхность  ориентирована вектором
ориентирована вектором 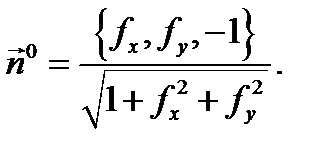 Учитывая, что
Учитывая, что 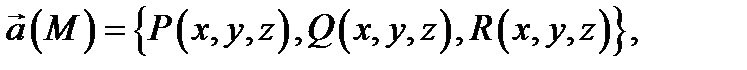 раскроем в (3) скалярное произведение:
раскроем в (3) скалярное произведение: 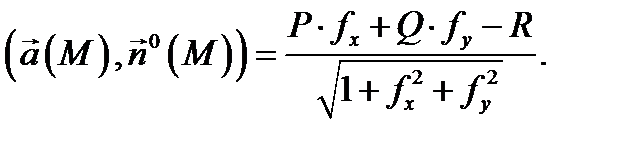 По теореме 1 имеем
По теореме 1 имеем
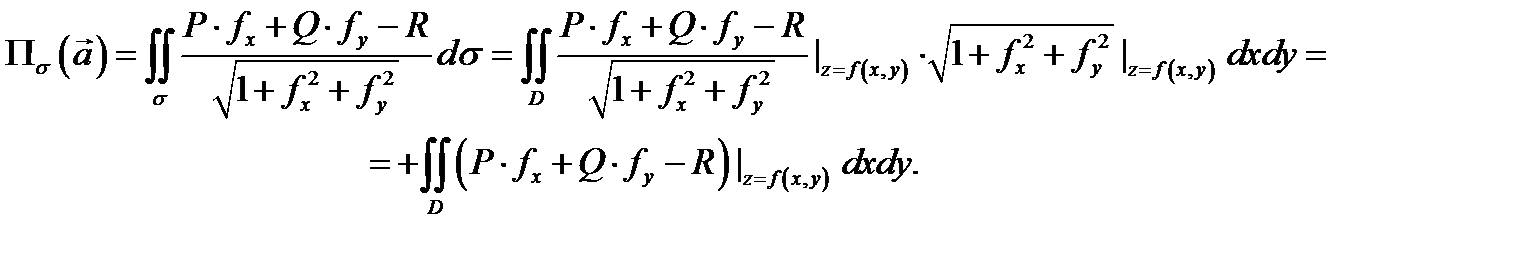
Теорема доказана.
Замечание 1. Если поверхность  задана неявно уравнением
задана неявно уравнением 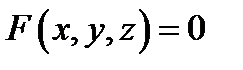 (где функции
(где функции 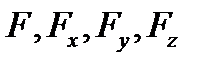 непрерывны, причем
непрерывны, причем 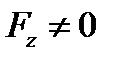 в области
в области 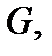 в которой лежит поверхность
в которой лежит поверхность  ), то
), то
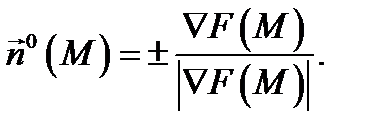 При этом знак выбирается в соответствии с ориентацией поверхности
При этом знак выбирается в соответствии с ориентацией поверхности  .
.
Дадим гидромеханический смысл потока: если 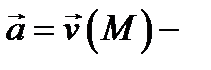 векторное поле скоростей жидкости, то
векторное поле скоростей жидкости, то 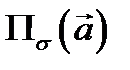 равен количеству жидкости, протекающей за единицу времени через поверхность
равен количеству жидкости, протекающей за единицу времени через поверхность  с ориентацией, определяемой нормалью
с ориентацией, определяемой нормалью 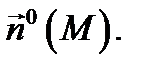
Пример 1 ( Кузнецов Л.А. Типовые расчеты ). Найти поток векторного поля 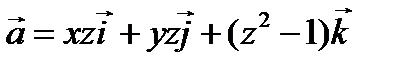 через поверхность
через поверхность 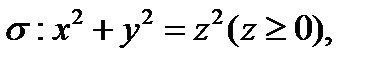 вырезаемую плоскостью
вырезаемую плоскостью 
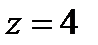 (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
(нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
Решение. Так как 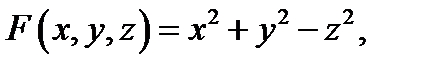 то нормаль к боковой поверхности
то нормаль к боковой поверхности  (конуса) будет иметь вид
(конуса) будет иметь вид 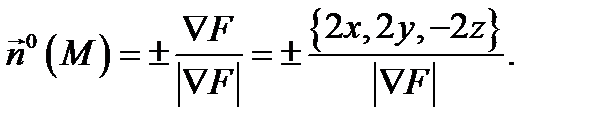 Выбор нормали должен быть таким, чтобы
Выбор нормали должен быть таким, чтобы 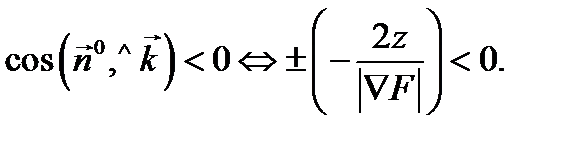 Так как в нашем случае
Так как в нашем случае 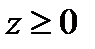 на поверхности
на поверхности  , то надо взять знак (+). Таким образом, нормаль будет такой:
, то надо взять знак (+). Таким образом, нормаль будет такой: 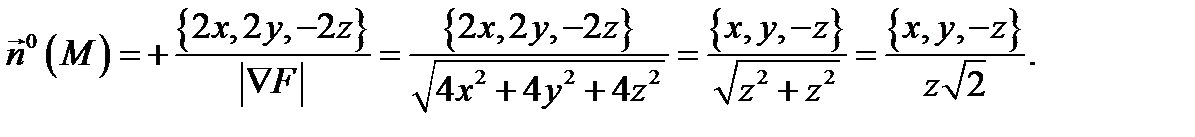 Здесь мы учли, что на поверхности
Здесь мы учли, что на поверхности  выполняется равенство
выполняется равенство 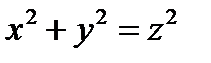 . Далее имеем
. Далее имеем
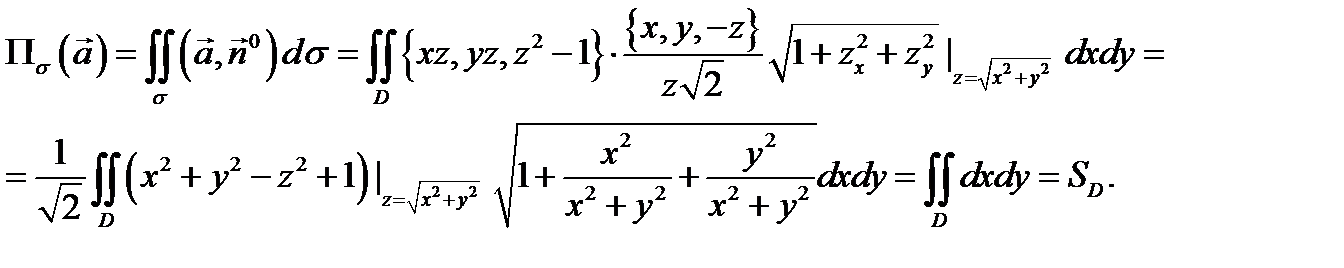
Область 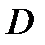 является проекцией поверхности
является проекцией поверхности  на плоскость
на плоскость 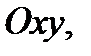 т.е. является кругом радиуса
т.е. является кругом радиуса 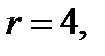 поэтому
поэтому