Численные методы решения дифференциальных уравнений в частных производных

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных

Одним из наиболее распространенных численных методов решения уравнений в частных производных является метод сеток. В методе сеток область Ω, в которой необходимо найти решение уравнения, разобьем прямыми, параллельными осям и , на прямоугольные области (рис.1.1), где

,

.

Точки, которые лежат на границе области Ω, называются внешними, остальные точки – внутренними. Совокупность всех точек называется сеткой, величины h и Δ – шагами сетки по хи t соответственно.

 

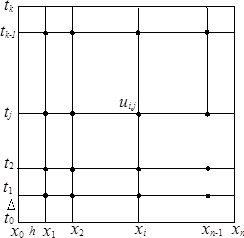
Рис.1.1. Сетка для области Ω

 

Идея метода сеток состоит в том, что вместо любой непрерывной функции будем рассматривать дискретную функцию , которая определена в узлах сетки , вместо производных функции будем рассматривать их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получим систему алгебраических уравнений. Чем меньше величины h иΔ, тем точнее получаемые алгебраические уравнения моделируют исходное дифференциальное уравнение в частных производных. В этом и последующих подразделах этой главы будет рассмотрен метод сеток для каждого из трех типов уравнений и его реализация в MATLAB. Знакомство с численными методами решения дифференциальных уравнений в частных производных начнем с разностных схем решения параболических уравнений.

Разностные схемы решения параболических уравнений будем рассматривать на примере следующего одномерного уравнения:

Построим сетку (см. рис.1.1). Для получения сеточного уравнения заменим производную приближенной разностной формулой:

.

В этой и последующих формулах – значение функции u в точке , – в точке , – в точке , – в точке , – в точке .

Для замены можно воспользоваться одной из приближенных разностных формул

;

.

Кроме того, заменим начальные и граничные условия их разностной аппроксимацией:

Заменив частные производные в задаче соответствующими разностными соотношениями, получим следующую вычислительную схему для расчета значений функции и в узлах сетки :

;

Это явная двухслойная разностная схема (рис.1.2).

Рис.1.2. Шаблон явной двухслойной разностной схемы

 

Учитывая, что на нулевом слое (при i = 0)все значения (как, впрочем, и ) известны, можно сначала явно рассчитать значения , затем и так до .Для устойчивости разностной схемы значения шагов по t и х должны удовлетворять следующему условию:

.

Пример. Решить параболическое уравнение, описывающее распределение температуры в стержне длиной L, начальная температура стержня задается произвольной функцией . Температуры концов стержня равны .

Здесь а² – коэффициент температуропроводности; – коэффициент теплопроводности материала стержня; с – удельная теплоемкость; – плотность массы.

Подпрограмма решения задачи с помощью явной разностной схемы в MATLAB:

//Правая часть дифференциального уравнения

function y=f(x, t)

y=sin(x*t)

endfunction

//Начальное условие

function y=fi(x)

y=exp(0.15*x)

endfunction

//Условие на левой границе

function y=myu(t)

y=l

endfunction

//Условие на правой границе

function y=nyu(x)

y=2.117

endfunction

function [u, x, t]=parabol(N, K, L, T, a)

//Функция решения параболического уравнения методом сеток с помощью явной разностной схемы. N - количество участков разбиения интервала по х (0, 1_); К – количество участков разбиения интервала по t (0, Т); а - коэффициент температуропроводности,

// Функция возвращает матрицу решений u вектора х, t

// Вычисляем шаг по х

H = L/N;

// Вычисляем шаг по t

Delta = T/K;

// Формируем массив х и первый столбец матрицы решений u

// из начального условия

for I = l: N+l

x(i) = (i-l)*h;

u(i, l) = fi(x(i));

end

//Формируем массив t, первую и последнюю строку матрицы решений u из граничных условий

for j = l: K+l

t(j) = (j-l)*delta;

u(l, j) = myu(t(j));

u(N+l, j) = nyu(t(j));

end

gam = a^{^}2*delta/h^{^}2;

// Формируем матрицу решений u

for j = l: K

for i = 2: N

u(i, j+l) = gam*u(i-l, j)+(l-2*gam)*u(i, j)+gam*u(i+l, j)+delta*...

f(x(i), t(j));

end

end

end

Входными данными подпрограммы parabol решения задачи являются: N – количество интервалов, на которые разбивается отрезок (О, L); К – количество интервалов, на которые разбивается отрезок (О, Т); L – длина стержня, Т – интервал времени, а – параметр дифференциального уравнения. Функция возвращает три параметра: решение – сеточная функция u, определенная на сетке , массивы x и t.

[U, Х, T]=parabol(50, 200, 5, 3, 0.4);

surf(X, T, U');

xlabel('X');

ylabel('T');

График решения данной задачи изображен на рис.1.3.

 

Рис.1.3. График решения параболического уравнения при

1.4.2. Использование метода сеток для решения гиперболических уравнений

Решение гиперболических уравнений также можно осуществить с помощью разностных схем. Разностные схемы решения одномерного гиперболического уравнения рассмотрим на примере следующего уравнения:

Построим сетку , в которой будем искать решение уравнения. Производную заменим соотношением:

,

остальные производные такие же, как и в предыдущем подразделе.

Получим следующую явную разностную схему решения уравнения:

Она устойчива при и по аналогии с разностной схемой (см. подразд. 1.4.1) может быть легко запрограммирована в MATLAB.

В качестве примера рассмотрим следующую задачу.

Пример. Решить начально-граничную задачу:

Ниже представлена функция giperbol решения данного уравнения, а на рис.1.4 – график полученного решения. Параметры функциианалогичны рассмотренным ранее, т.е. в подпрограмме решения параболического уравнения.

function [u, x, t]=giperbol(N, K_/L, T, a)

//Функция решения гиперболического уравнения с помощью явной разностной схемы. Входные данные: N - количество участков разбиения интервала (0, L); K - количество участков разбиения интервала (0, T); a - коэффициент теплопроводности; u - матрица решений в узлах сетки; массив x; массив t,

// Вычисляем шаг по х и по t

h=L/N; delta=T/K;

//Формируем массив x, первый и второй столбцы матрицы решений u из начального условия

for i=1: N+1

x(i)=(i-1)*h;

u(i, 1)=fi(x(i));

u(i, 2)=u(i, 1)+delta*psi(x(i));

end

//Формируем массив t, первую и последнюю строки матрицы решений u из граничных условий

for j=1: K+1

t(j)=(j-1)*delta;

end

//Формируем первую и последнюю строки матрицы решений u из граничных условий

for j=2: K+1

u(1, j)=0;

u(N+1, j)=fi(L);

end

gam=a^2*delta^2/h^2;

//Формируем матрицу решений u

for j=2: K

for i=2: N

u(i, j+1)=-u(i, j-1)+gam*u(i-1, j)+(2-2*gam)*... u(i, j)+gam*u(i+1, j)+delta^2*f(x(i), t(j));

end

end

end

Рис.1.4. График решения гиперболического уравнения

 

1.4.3. Использование метода сеток для решения эллиптических уравнений

Разностные схемы решения одномерного эллиптического уравнения рассмотрим на следующем примере.

Пример. Рассмотрим разностную схему для эллиптического уравнения в прямоугольной области с граничными условиями Дирихле на границе Г:

Проведем в области Ω прямые, параллельные осям и , где ;

Для построения разностного уравнения заменим частные производные и граничные условия следующими соотношениями:

Преобразуем данную эллиптическую краевую задачу к следующей системе разностных уравнений:

Эту систему можно решать итерационными методами (например, методом Зейделя). В случае медленной сходимости итерационных процессов при решении сеточных уравнений, получаемых при аппроксимации гиперболических и эллиптических задач, можно попробовать заменить метод Зейделя градиентными методами (или методами релаксации). Ниже представлено решение эллиптического уравнения сеточным методом, а на рис.1.5 график полученного решения.

Рис.1.5. График решения эллиптического уравнения

 

function [psi, x, y, k]=ellip(R, a, b, Nx, Ny, eps)

// Функция ellip решения задачи

// Входные данные: R, a, b - значения, определяющие область решения задачи; Nx - количество участков разбиения интервала(R-b, R+b); Ny - количество участков разбиения интервала(-a, a); eps - точность решения уравнения методом Зейделя.

// Выходные данные:

// psi - матрица решений в узлах сетки, массив x, массив y, k - количество итераций при решении разностного уравнения

// Вычисляем шаг по y и по x

hy=2*a/Ny; hx=2*b/Nx;

// Формируем массив x, первый и последний столбцы матрицы решений psi из граничного условия

for i=1: Nx+1

x(i)=R-b+(i-1)*hx;

psi(i, 1)=0; psi(i, Ny+1)=0;

end;

// Формируем массив y, первую и последнюю строки матрицы решений psi из граничного условия

for j=1: Ny+1

y(j)=-a+(j-1)*hy;

psi(1, j)=0; psi(Nx+1, 1)=0;

end;

// Вычисляем коэффициенты разностного уравнения

A=2/hy^2+2/hx^2;

D=1/hy^2;

for i=2: Nx+1

B(i)=1/hx^2+5/(2*hx*x(i));

C(i)=1/hx^2-5/(2*hx*x(i));

end

//Решение разностного уравнения методом Зейделя

p=1;

k=0;

while p> eps

for i=2: Nx

for j=2: Ny

V=1/A*(B(i)*psi(i-1, j) +C(i)*psi(i+1, j)+ D*(psi(i, j-1)...+psi(i, j+1))+2);

R(i, j)=abs(V-psi(i, j));

psi(i, j)=V;

end

end

p=R(2, 2);

for i=2: Nx

for j=2: Ny

if R(i, j)> p

p=R(i, j);

end

end

end

k=k+1;

end

endfunction

//Вызов функции решения задачи.

[PSI, X, Y, K]=ellip(18, 3, 6, 32, 16, 0.01);

//Построение графика функции

surf(X, Y, PSI');

xlabel('X');

ylabel('Y');

⇐ Предыдущая1234567Следующая ⇒

Поделиться: