
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Закон связи объема и содержания понятия ⇐ ПредыдущаяСтр 3 из 3
 «Всякое изменение содержания понятия ведет к обратному изменению его объема и наоборот, всякое изменение объема понятия ведет к обратному изменению его содержания».
   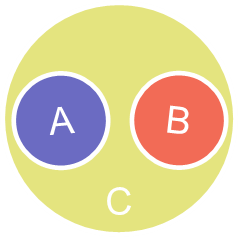    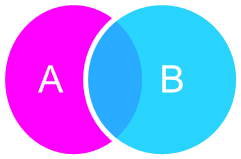 [4] Отношения между понятиями [4] Отношения между понятиями
[5] ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ Операции обобщения и ограничения Операция деления и её правила 3) определение понятий Мышление в собственном значении слова означает процесс оперирования понятиями. Поэтому так важно овладеть данным процессом, а именно · операциями обобщения и ограничения; · операцией деления и её правилами; · методикой и правилами определения понятий Обобщение и ограничение понятий Обобщение – этологическая операция, состоящая в переходе от понятия с меньшим объёмом, но с большим содержанием, к понятию с большим объёмом, но меньшим содержанием Пример обобщения: роза (А) - цветок (Б) - растение (В) - живой организм (Г) - организм (Д) - предмет (Е)
Ограничение – это логическая операция перехода от понятия с большим объёмом, но с меньшим содержанием, к понятию с меньшим объёмом, но большим содержанием Пример ограничения: - произведение музыкального искусства (Е) - опера (Д) - опера русского композитора (Г) - опера русского композитора XIX века (В) - опера Мусоргского Модеста Петровича (Б) - опера Мусоргского М. П. «Хованщина» (А)
Можно обе рассматриваемые нами операции изобразить и такой схемой:
Назначение операций обобщения и ограничения заключается в том, что они придают определённость мышлению, подчиняя его элементарным правилам: 1) обобщение правильно, если мысль осуществляет переход от видового понятия к родовому; 2) ограничение правильно, если мысль осуществляет переход от родового понятия к видовому ЗАПОМНИТЕ: ОПЕРАЦИИ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ОСУЩЕСТВЛЯЮТСЯ ТОЛЬКО МЕЖДУ ПОНЯТИЯМИ, КОТОРЫЕ НАХОДЯТСЯ В ОТНОШЕНИЯХ ПОДЧИНЕНИЯ Логические ошибки: 1) Обобщение и ограничение часто смешивают с мысленным переходом от части к целому и выделением части из целого 2) Ограничение понятий часто происходит с помощью добавления признака: «студент» - «добросовестный студент». Но имейте в виду, что нередко добавление эпитета не ведёт к ограничению понятия и является излишним: «девушка» - «молодая девушка» (а кто видел старых девушек? ), «шар» - «круглый шар» (а какие ещё шары бывают? ) Данная ошибка называется плеоназмом (излишеством)
Деление понятий Для упорядочения знания, поиска закономерных связей и уточнения смысла многих слов человеческим мышлением используется такая интеллектуальная процедура как классификация Классификация – это распределение предметов какого-либо рода на взаимосвязанные группы (классы) согласно наиболее существенным признакам, присущим предметам данного рода и отличающим их от предметов других родов; при этом каждый класс занимает в получившейся системе своё постоянное, определённое место В основе любой классификации лежит такая логическая процедура как деление понятий – это логическая операция, раскрывающая объём понятия Структура деления: 1) Делимым называется родовое понятие, в объёме которого выделяются возможные виды 2) Основание деления – признак, в соответствии с которым выделяются члены деления 3) Члены деления – полученные в результате самой операции соподчинённые виды Виды деления: 1) Деление по наличию или отсутствию признака, служащего основанием деления (его называют часто дихотомическим делением) 2) Деление по видоизменению признака, положенного в основание этой операции 3) Смешанное деление, когда используются оба вида деления одновременно Примеры дихотомического деления: · государства можно разделить на демократические и недемократические, · людей – на счастливых и несчастливых, · школьников – на добросовестных и недобросовестных, · предпринимателей – на удачливых и неудачливых, · граждан – на дееспособных и недееспособных
Право может быть оформлено (признак – форма выражения) в виде: · правового обычая, · юридического прецедента, · нормативного акта, · международного договора Людей по социально-классовому признаку можно разделить на: · крестьян, · наёмных работников, · предпринимателей, · лиц свободных профессий Смешанное деление, когда используются оба вида деления одновременно 1) политические институты делятся на государственные и негосударственные; 2) среди негосударственных различаются партийные и непартийные; 3) непартийные же включают в себя профессиональные, женские, молодёжные, спортивные, художественные и так далее Основные правила и ошибки деления: 1) Правило соразмерности 2) Правило исключения 3) Правило одного основания: 4) Правило непрерывности 1)Правило соразмерности – объединение объёмов членов деления должно совпадать с объёмом делимого понятия или объём делимого должен полностью исчерпываться членами деления. (А = В1 + В2 + В3 +... + Вn) Это означает, что при делении: a) не должно быть пропущено ни одного предмета из объёма делимого понятия; b) не должно появиться ни одного лишнего члена деления Если данное правило не соблюдается, то возможны две основные ошибки: A. Неполное деление B. Обширное деление (или деление с лишними членами) А. Неполное деление – деление, при котором среди членов деления не достаёт какого-либо вида предметов, выделяемого по данному признаку Например, если Вам скажут, что имеются две мировые религии (А): ислам (В) и христианство (С), - то это будет значит, что допущена и содержательная, и логическая ошибка: Вам не назвали буддизм В. Обширное деление – деление, при котором объём делимого понятия является частью объединения объёмов членов деления Пример:
2)Правило исключения – члены деления должны исключать друг друга или каждый элемент объёма делимого понятия должен входить только в один член деления Это означает, что члены деления должны быть только несовместимыми и соподчинёнными понятиями Если члены деления не исключают друг друга, то это означает логическую ошибку. Нельзя часы делить на наручные, настенные, башенные, настольные, золотые, песочные, подарочные, командирские 3)Правило одного основания – деление должно проводиться только по одному признаку.
 4)Правило непрерывности – в процессе деления всегда следует переходить к ближайшим видам
3) В процессе ДЕЛЕНИЯ раскрывается ОБЪЁМ ПОНЯТИЯ. Но чтобы научиться работать с понятием, необходимо уметь раскрыть и его СОДЕРЖАНИЕ Осуществляется это с помощью логической операции ОПРЕДЕЛЕНИЯ ПОНЯТИЙ Определение понятий – это логическая операция, раскрывающая основное в некотором отношении содержание понятия посредством перечисления входящих в него простых признаков. Определение понятия есть вместе с тем раскрытие сущности соответствующего предмета. Пример: «Конституция есть основной закон государства, устанавливающий его общественное и политическое устройство» «Холдинг - компания, владеющая контрольным пакетом акций других компаний с целью контроля и управления их деятельностью» Структура определения: Всякое определение состоит из двух элементов, тесно связанных друг с другом: определяемого (definiens) и определяющего (definiendum) Определяемым – является то, ЧТО скрывается в определении - предмет, понятие или слово Определяющим – Служат ТЕ общие и существенные ПРИЗНАКИ, которые составляют содержание определяемого Логическая связь между определяемым и определяющим выражается в русском языке словами «есть», «является», «называется» Виды определений: A. По характеру определяемого (definiens) различают номинальные и реальные определения B. По характеру определяющего (definiendum) выделяются явные и неявные определения А. Реальные определения даются уже так или иначе знакомым нам понятиям Номинальные определения даются только новым понятиям или новым словам Реальное есть определение самого предмета, отражённого в соответствующем понятии «Бюджет - роспись денежных доходов (поступлений) и расходов (использования), составляемая для государства, местных органов управления, предприятий, учреждений, семей или отдельного лица на определённый период (год, квартал, месяц)» Большинство определений, с которыми мы имеем дело в гуманитарных дисциплинах – реальные. В нашей душе существует некоторое не вполне отчётливое представление об объёме и содержании большинства понятий, поэтому с помощью определений мы пытаемся выразить это своё представление в более или менее точных терминах. Образцы этих определений смотрите в энциклопедических словарях-справочниках Номинальные – определение, создающее содержание вновь вводимого термина или имени. Образцы номинальных определений дают всевозможные толковые словари, а также словари иностранных слов По характеру определяющего (definiendum) выделяются явные и неявные определения Зависит характер определяющего от объёма того понятия, которое мы определяем Все понятия по объёму делятся на единичные и общие. ЯВНЫЕ ОПРЕДЕЛЕНИЯ ДАЮТСЯ ПРЕИМУЩЕСТВЕННО ОБЩИМ ПОНЯТИЯМ В. Явные – определения, раскрывающие существенные признаки предмета Большая часть понятий, с которыми имеет дело логика – явные В ЯВНЫХ ОПРЕДЕЛЕНИЯХ ОПРЕДЕЛЯЕМОЕ ОБЯЗАТЕЛЬНО ДОЛЖНО БЫТЬ ТОЖДЕСТВЕННО (РАВНО) ОПРЕДЕЛЯЮЩЕМУ
ПРАВИЛА И ОШИБКИ ОПРЕДЕЛЕНИЯ ПОНЯТИЙ Правило соразмерности В правильном определении объёмы definiens и definiendum должны совпадать. Definiendum и definiens можно переставить местами – смысл определения не должен меняться Пример: «Квадрат есть прямоугольник, у которого все четыре стороны равны». Меняем определяемое и определяющее местами. Получается: «Прямоугольник, у которого все четыре стороны равны, является квадратом» Так как объёмы двух частей определения тождественны, равны, то при перемене их смысл данного определения не изменился Нарушение же правила соразмерности приводит к следующим ошибкам: 1) Слишком широкое определение, когда определяющее понятие (А) по объёму шире определяемого (Б)
Получилось: «Всякое хищение чужого имущества есть кража». Но, увы, под это определение подойдут и грабёж (В), и мошенничество (Г), и разбой (Д). А это разные виды преступления, называемого кражей 2) Слишком узкое определение, когда определяемое понятие (А) по объёму шире определяющего (Б) 1. «Кража есть тайное хищение чужих денег» (если не укажем других видов имущества) 2. «Вершина – самая высокая часть холма» (если не укажем: «и горы») 3. «Совесть есть осознание человеком нравственной ответственности перед самим собой за свои действия и поступки» (если не укажем: «и перед обществом») 3) Определение в одном отношении широкое, в другом – узкое Пример: «Кража есть хищение денег». Здесь мы не указали, с одной стороны - «тайное», а с другой стороны - «различных видов имущества» 4) Правило неотрицательности. Оно означает, что в определении нельзя ограничиваться одними отрицательными признаками. При нарушении правила следует логическая ошибка: «Определение только отрицательное». Отрицательные признаки в определении могут быть, но если ими ограничимся, то определение будет не ясным. Если на вопрос: «Что такое право? » Вы получите ответ: «Право это не философия, не логика, не искусство и не мораль», - то, видимо, такое определение не очень-то прояснит Ваши представления о праве 5) Правило запрета круга При нарушении правила могут быть две логические ошибки: 1) Тавтология Примеры: «Смешное – это то, что вызывает смех» «Количество - характеристика предмета с его количественной стороны». «Коллегия адвокатов - объединение лиц, занимающихся адвокатской деятельностью» 2) Круг в определении Это более завуалированная ошибка, когда определяющее понятие само раскрывается через определяемое Если право определить, как «систему норм, имеющую своей задачей охранять и оправдывать существующий правопорядок», то не исключено, что правопорядок вскоре придётся определять через право. Тогда и возникнет круг в определении. 6) Правило ясности На лекции по основам экономики преподаватель применяет новое для Вас слово, например, «хеджирование» Что будет, если преподаватель ограничится вполне понятным для него определением: «Хеджирование - это страхование от возможных потерь при колебании цены товара на рынке реального товара посредством купли фьючерсных контрактов»? Мало ясности и во многих роскошных определениях - афоризмах. Таких как это: «Ясность - вот лучшее украшение истинно глубокой мысли». Ошибка, которая возникает при нарушении рассмотренного правила, так и называется: «определение через неизвестное».
Тема 3 Суждение как форма мышления Ø [1] Суждение в логике. Общая характеристика Ø [2] Простые суждения Ø [3] Сложные суждения
[1] Суждение — это форма мысли, в которой утверждается или отрицается существование предметов, связь между предметами и их признаками, отношения между предметами Языковой формой выражения суждение является предложение Суждение — это смысловая сторона предложения, но не тождественная единица Всякое суждение выражено в повествовательном предложением содержащим сообщение о чем-либо, как и предложение суждение бывают простые и сложные · Простые – это суждение выражающие связь двух понятий · Сложные – образуются из нескольких простых при помощи логических союзов [2] В простом суждении выражается связь двух понятий. Имеются следующие структурные элементы: 1. Субъект суждения — это понятие о предмете суждения, то есть то, о чем говорится в суждении [S] 2. Предикат суждения — это понятие признака предмета, то есть то, что говорится о субъекте суждение [P] 3. Связка выражает отношение между S и P. Бывает утвердительной или отрицательной обозначается словами «есть/не есть», «суть/не суть» и так далее " тире", группы слов, простым согласование слов. 4. Квантор указывает на отношение суждения ко всему объему понятия выражая субъект или его часть. Квантор общности [ɏ ] (все…) Квантор существования [Ǝ ] (некоторые…)
Виды простых суждений 1. Атрибутивные/суждения свойства. Они содержит в себе знания о свойствах предметов или принадлежности предметов к определённому классу 2. Суждение отношения/релятивные. Выражают различные отношения между предметами по месту, величине, времени, причин зависимости и так далее 3. Суждение существования/экзистенциальный. Это суждение который содержит информацию о наличии или отсутствии предмета наши мысли в реальности " бог есть" и " есть ли жизнь на Марсе"
Суждение имеет 2 основных характеристики ü Количество ü Качество Качество зависит от связки между субъектом и предикатом поэтому по качеству суждения могут быть утвердительные или отрицательные Количество — это характеристика показывает в каком объеме входит в суждение его субъект. По количеству делится на частные, общие и единичные. Единичные в логическом анализе приравниваются к общим поэтому логике классифицируются по количеству только частные и общие
Количественную сторону суждение определяет через кванторное слово
Термином категоричности суждения является субъект и предикат Термин считается распределённым если он рассматривается в данном суждение во всём объеме, в противном случае термин не распределён
Термин рассматривается в суждении во всём объеме если он полностью включён в объем другого понятия или полностью исключён из него
· Количество частное ·
· Количество частное · качество утвердительное
Если в одном суждении встречается хотя бы один термин не входящий в другое суждение, то такие два суждения называют несравнимыми У сравнимых суждениях совпадают оба термина (субъект и предикат)
Сравнимые суждение делятся на совместимые и не совместимые Сравнимые суждение совместимы если они могут быть единовременно истинными Несовместимые если они не могут быть вместе истинны В свою очередь совместимые суждение могут находиться в отношении подчинения и субконтрарности Несовместимые на отношения противоположности и противоречивости Из логического квадрата следует что частные суждения подчиняется общим поэтому истинность общего суждения определяет истинность частного, но ложность общего суждения оставляет частное неопределённым Истинность частного суждения также оставляет общее неопределённым Ложность частного суждения обусловлено ложности общего
В отношении частичного совпадение действует следующие правило: · Оба они одновременно могут быть истинными, но не могут быть одновременно ложными если одно из них ложно, то и другое обязательно истинно, но если одно из них истинно, то другое неопределенно Для отношения противоречивости действует правило: · Два противоречивых суждения не могут быть одновременно истинными и одновременно ложными Для отношений противоположности: · Если одно из противоположных субъектов истинно, то другое будет ложным, однако ложность одного из них оставляет другое суждение неопределённым
[3] Сложные суждения – это суждения которые состоят из двух или нескольких простых связанных логическими союзами Зависимости от логических союзов выделяют: 1. соединительные сложные суждения (конъюнкция) 2. Условное (союзу " если, то" ) 3. Разделительное (дизъюнкция) 4. Отрицательное (логический союз с НЕ) 5. Эквивалентное (эквиваленция) Также сложное суждение делится по модальности, то есть по характеру выраженного в них знания
Тема 4 Законы логики
|
Последнее изменение этой страницы: 2017-04-12; Просмотров: 724; Нарушение авторского права страницы