
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Закон Био-Савара-Лапласа. Магнитное поле прямолинейного и кругового токов.
Закон Био-Савара-Лапласа позволяет вычислить магнитную индукцию поля, созданного элементом тока Id
dB = т.е. индукция магнитного поля, создаваемого элементом тока Id Закон Био - Савара - Лапласа в векторной форме имеет вид: d Закон Био - Савара - Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля
Применим закон Био - Савара - Лапласа и принцип суперпозиции (14-7) к расчету магнитных полей следующих токов: 1) Магнитное поле прямолинейного тока. Из рис.14.4 с учетом (14-6) находим, что d интегрируя последнее равенство, получаем
Для бесконечно длинного проводника
2) Магнитное поле кругового тока. Можно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (рис.14.5), будет
В частности, в центре кругового тока
Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки
При больших расстояниях от контура, т. е. при r0 > > R из (14-10) получим
Циркуляция вектора магнитной индукции. Поле соленоида и тороида Для электростатического поля
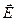 вдоль замкнутого контура L равна нулю. Можно показать, что циркуляция вектора вдоль замкнутого контура L равна нулю. Можно показать, что циркуляция вектора  вдоль замкнутого контура L равна алгебраической сумме токов, охватываемых контуром, умноженной на вдоль замкнутого контура L равна алгебраической сумме токов, охватываемых контуром, умноженной на  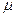 0, т. е. 0, т. е.
Поскольку Применим теорему о циркуляции для вычисления индукции магнитного поля соленоида и тороида. 1) Поле соленоида Соленоидом, (рис.14.7), называется цилиндрическая катушка, на которую вплотную намотано большое число витков провода. Пусть N - число витков вдоль длины соленоида l, тогда или Интегралы на участках 1-2, 3- 4 равны нулю, т.к.
интеграл на участке 4-1 равен нулю, т.к. вне соленоида индукция B= где n=N / l - число витков, приходящееся на единицу длины соленоида. Поле соленоида однородно. 2) Поле тороида Тороид (рис.14.8), представляет тонкий провод, плотно навитый на каркас, имеющий форму тора. Для него где R - радиус средней линии тора, отсюда B = Поле тороида неоднородно: оно уменьшается с увеличением r. Поле вне тороида равно нулю. Магнитный поток. Теорема Гаусса Для однородного магнитного поля, пронизывающего плоскую поверхность площади S, ( см. рис. 4 ). магнитный поток Ф= где
dФ = Магнитный поток сквозь произвольную поверхность Ф= В природе нет магнитных зарядов и поэтому теорема Гаусса для магнитного потока имеет вид Ф = т.е. магнитный поток сквозь произвольную замкнутую поверхность равен нулю. Пусть в формуле (14-17) |
Последнее изменение этой страницы: 2017-05-05; Просмотров: 559; Нарушение авторского права страницы