Парная регрессия и метод наименьших квадратов

Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными Y и X. Т.е. имеем модель парной регрессии в виде:

Y_i =a+bX_i+u_i, i=1, …, n.

а. Eu_i=0, i=1, …, n.

б.

в. X₁, …, X_n – неслучайные величины.

Предположим, что имеется выборка значений Y и X.

Обозначим арифметические средние (выборочные математические ожидания) для переменных X и Y:

.

Запишем уравнение оцениваемой линии в виде:

, (2.6)

где и - оценки неизвестных параметров a и b, а - ордината этой линии.

Пусть (X_i, Y_i) одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно e_i=Y_i - .

Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок и , для которых сумма квадратов отклонений для всех точек становится минимальной.

Y

 

 

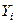
X

 

Рис. 2.1. Иллюстрация принципа МНК

 

Необходимым условием для этого служит обращение в нуль частных производных функционала:

по каждому из параметров. Имеем:

Упростив последние равенства, получим стандартную форму нормальных уравнений, решение которых дает искомые оценки параметров:

(2.7)

Из (2.7) получаем:

(2.8)

Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).

Таблица 2.1

Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)

Год	Индивидуальное потребление, млрд. долл.	Личные доходы, млрд. долл.

 

Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются , затем x_i, y_i. Результаты заносятся в столбцы 3 и 4. Далее определяются x_i², x_iy_i и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров =43145/46510=0, 9276; =321, 75-0, 9276^.350=-2, 91.

Оцененное уравнение регрессии запишется в виде =-2, 91+0, 9276X.

Следующая важная проблема состоит в том, чтобы определить, насколько " хороши" полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.

Относительно квалифицирования уравнения =-2, 91+0, 9276X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой.

Таблица 2.2

Рабочая таблица расчетов (по данным табл. 2.1)

 

Год	X	Y	x	y	x2	xy		ei
			-93	-85, 75		7974, 75	235, 48	0, 52
			-75	-67, 75		5081, 25	252, 18	1, 82
			-57	-54, 75		3120, 75	268, 88	-1, 88
			-41	-40, 75		1670, 75	283, 72	-2, 72
			-31	-31, 75		984, 25	292, 99	-2, 99
			-13	-10, 75		139, 75	309, 69	1, 31
				3, 25			321, 75	3, 25
				13, 25		185, 5	334, 74	0, 26
				33, 25		1163, 75	354, 22	0, 78
				53, 25		2928, 75	372, 77	2, 23
				79, 25		6894, 75	402, 45	-1, 45
				109, 25		13000, 75	432, 13	-1, 13
å	=350, 00	=321, 75		0, 00			=321, 75	0, 00

 

Полученное уравнение =-2, 91+0, 9276X можно использовать для расчета точечного прогноза, в том числе и на ретроспективу. Подставляя последовательно значения X из второго столбца табл. 2.2 в уравнение =-2, 91+0, 9276X, получим предпоследний столбец табл. 2.2 для прогнозных значений . Ошибка прогноза вычисляется по формуле e_i=Y_i - и дана в последнем столбце рабочей таблицы.

Заметим, что ошибка прогноза e_i фактически является оценкой значений u_i. График ошибки e_i представлен на рис. 2.2. Следует отметить факт равенства нулю суммы Se_i=0, что согласуется с первым ограничением модели парной регрессии - Eu_i=0, i=1, …, n. Ñ

Рис. 2.2. График ошибки прогноза

 

В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:

q регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней - Y_i =a₀ + a₁X_i + a₂X_i²+ u_i, i=1, …, n или гипербола - Y_i =a₀ + a₁/X_i + u_i, i=1, …, n;

q регрессии нелинейные по оцениваемым параметрам, например степенная функция - Y_i =a₀ u_i, i=1, …, n, или показательная функция - Y_i = , i=1, …, n.

В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Y_i =a₀ + a₁X_i + a₂X_i²+ u_i переменной X_i² на X_1i: X_i²=X_1i, получаем линейное уравнение регрессии Y_i =a₀ + a₁X_i + a₂X_1i+ u_i, i=1, …, n.

Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Y_i =a₀ u_i после логарифмирования получаем линейную функцию в логарифмах и применяем МНК.

Однако для, например, модели Y_i =a₀+a₂ +u_i линеаризующее преобразование отсутствует, и приходится применять другие способы оценивания (например, нелинейный МНК).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: