Расчет начального действующего значения периодической составляющей тока трехфазного короткого замыкания в цепи статора синхронного генератора в предположении отсутствия у него демпферных обмоток

 

Рассмотрим баланс магнитных потоков в продольной оси ротора синхронной машины при установившемся симметричном режиме ее ра­боты с отстающим по фазе током и в начальный момент трехфазного короткого замыкания. Будем считать, что на роторе, кроме обмот­ки возбуждения, никаких других контуров не имеется (нет демпфер­ных обмоток). При отсутствии насыщения каждый из потоков и их составляющие можно рассматривать независимо друг от друга. Полный поток, создаваемый током, протекающим по обмотке возбуждения, (рис. 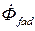6.2, 7.1) состоит из полезного потока и потока рассеяния . Продольный поток в воздушном зазоре по­лучим, сложив с потоком 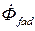навстречу направленный ему поток продольной реакции статора 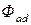(размагничивающая реакция ста­тора при индуктивном характере нагрузки). Результирующий магнит­ный поток 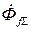, сцепленный с обмоткой возбуждения, складывает­ся из потока и потока рассеяния .

В начальный момент КЗ из-за уменьшения сопротивления внешней цепи периодические слагающие токов фаз статора скачком возраста­ют, вызывая увеличение потока продольной реакции статора на ве­личину . Возникающие одновременно апериодические слагаю­щие токов обеспечивают в момент нарушения режима сохранение пред­шествующего мгновенного значения тока. Создаваемый ими магнитный поток практически неподвижен в пространстве и в балансе не участ­вует, так как рассматриваются составляющие потока, неподвижные по отношению к ротору, т.е. вращающиеся с синхронной скоростью.

В соответствии с законом Ленца приращение потока вы­зовет ответную реакцию обмотки возбуждения: в ней наводится свободный ток такой величины и направления, чтобы результирующий поток, сцепленный с этой обмоткой, в начальный момент КЗ сохранил то же значение, что и в нормальном предшествующем режиме. Свобод­ный ток обмотки возбуждения вызывает приращение потока на величину , равную и противоположно направленную прира­щению . При этом пропорционально увеличиваются

состав­ляющие потока 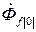: полезный поток 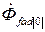и поток рассеяния 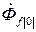что приводит к уменьшению потока в воздушном зазоре до . Однако результирующий поток 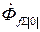, сцеп­ленный с обмоткой возбуждения, как видно из рис. 7.1, сохраняет свое предшествующее значение 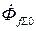. Такое же соотношение соблю­дается и между соответствующими потокосцеплениями обмотки возбуждения:

­

 

.

Выразим результирующие потокосцепления в продольной оси d статорной и роторной обмоток через соответствую­щие составляющие токов и индуктивности. Будем считать все величи­ны ротора приведенными к статору и выраженными, как и величины статора, в относительных единицах (при этом, в частности, индук­тивность численно равна индуктивному сопротивлению ; знак относительной величины будем опускать).

;

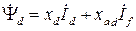(4-1)

.

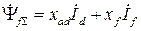Здесь полное индуктивное сопротивление обмот­ки возбуждения;

- индуктивное сопротивление рассеяния обмотки воз­буждения, приведенное к статору;

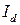- продольная составляющая тока статора.
Определим из второго уравнения (4.1) ток возбуждения:

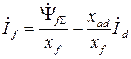
и подставим его в первое уравнение:

.

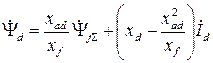В нормальном предшествующем режиме этим потокосцеплениям соответствуют ЭДС и напряжения:

.

Введем обозначения:

- составляющая напряжения предшествующего режима по поперечной оси ротора;

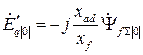- поперечная переходная ЭДС предшествующего режима.

Индуктивное сопротивление

называют продольным переходным сопротивлением, оно является параметром синхронной машины. С учетом введенных обозначений получаем выражение для переходной ЭДС:

, (4-2)

по которому она может быть вычислена, если известны параметры предшествующего режима и .

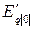Поскольку результирующее потокосцепление обмотки возбуждения в начальный момент переходного процесса сохраняет свое предшествующее значение , то и переходная ЭДС , пропорциональная этому потокосцеплению, в начальный момент вне­запного нарушения режима остается той же, что и в предшествующем режиме:

,

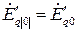т.е. скачком изменяться не может. Тем самым переходная ЭДС позволяет связать предшествующий режим с новым (от внезапного из­менения) режимом машины, в чем заключается ее особая практическая ценность, хотя она и является расчетной, условной ЭДС, которую нельзя измерить. Ее можно выделить в любой момент произвольного процесса, но именно в начальный момент внезапного нарушения режи­ма благодаря своему свойству не претерпевать никаких скачкообраз­ных изменений она совместно с сопротивлением особенно удоб­на для представления синхронной машины схемой замещения.

На рис. 7.2 приведена векторная диаграмма явнополюсной машины в нормальном установившемся режиме при нагрузке ее с отстающим током, из которой графически можно получить величину . По­рядок ее построения следующий: известны величины напряжения 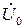, тока 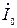и угла , между их векторами, с которыми машина работает в предшествующем режиме. Продлеваем направление вектора тока 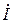и из конца вектора опускаем на эту прямую пер­пендикуляр, затем продлеваем его в другую сторону и от конца вектора 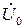откладываем по направлению перпендикуляра вектор . Соединив прямой начало вектора и конец вектора 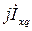, получаем направление оси q, а, следовательно, и оси d, пер­пендикулярной оси q ротора. Проектируя векторы и 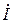на оси d, q, получаем их составляющие , , , 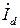. Добавив к концу вектора , в соответствии с выражением (4-2) вектор 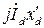, получаем вектор ЭДС .

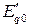Выражение для продольного переходного сопротивления можно пре­образовать

, (4-3)

откуда видно, что 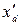представляет собой результирующее индук­тивное сопротивление статорной обмотки при закороченной обмотке возбуждения.

Схему замещения синхронной машины в продольной оси ротора в начальный момент КЗ получим, введя в цепь обмотки возбуждения (рис. 7.3) ЭДС пропорциональную результирующему потокосцеплению этой обмотки. После замены ветвей с 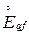, и одной эквивалентной получаем схему рис. 7.4, где, как и следовало ожидать, машина представлена своими и (сравнить со схемой замощения для установившегося режима рис. 6).

В поперечной оси ротора при отсутствии замкнутых контуров

и таким образом, для отдельно работающей синхронной машины без демпферных обмоток начальное значение периодической слагающей то­ка КЗ, называемое начальным переходным током, вычисляется по фор­муле

, (4-4)

где - индуктивное сопротивление внешней цепи;

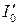- действующее значение начального переходного тока.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться: