
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Кинематика абсолютно твердого тела
Движение твердого тела можно рассматривать как сумму поступательного и вращательного движений. Движение твердого тела называют поступательным, если любая прямая, жестко связанная с телом, перемещается, оставаясь параллельной ее первоначальному направлению. При вращении точки тела описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Для описания вращательного движения вводят понятие угловой скорости и углового ускорения. Отношение Мгновенная угловая скорость
Вектор угловой скорости направлен по оси вращения, так что его положительное направление составляет с направлением вращения правовинтовую систему, т. е. подчиняется правилу буравчика.
Если
Частота вращения показывает число оборотов тела в единицу времени:
откуда
У гловое ускорение
Угловое ускорение вводят при неравномерном вращении. Если за время
Мгновенное угловое ускорение
Из этой формулы следует, что вектор углового ускорения направлен по оси вращения.
Нормальное ускорение:
Сопоставим основные уравнения и величины кинематики вращательного движения тела вокруг неподвижной оси и его поступательным движением, подчеркнув их аналогию.
Примеры решения задач Задача 1. Закон движения материальной точки имеет вид
где А = 4 м/с; С = 1 м/с2; В = 5 м/с; D = 1 м/с3.
Найти абсолютное значение скорости в момент t = 2 с.
Решение По условию задачи компоненты радиус-вектора
Абсолютное значение скорости
где
Задача 2. Самолет летит из пункта А в В, расположенный южнее А на 150 км, и возвращается обратно. Определить продолжительность полета, если известно, что во время рейса ветер дул с запада на восток. Скорость самолета 360 км/ч, скорость ветра 30 м/с.
Решение
| |||||||||||||||||||
| t = ? | |||||||||||||||||||
Относительно системы отсчета, связанной с Землей
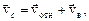
где 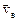 – скорость ветра;
– скорость ветра;
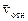 – скорость самолета относительно ветра.
– скорость самолета относительно ветра.
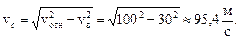
Время движения из пункта А в пункт В:
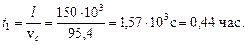
Самолет вернется в пункт А через t = 2t1 = 0,88 час.
Задача 3. С крыши дома высотой Н = 10 м вертикально вверх брошено тело с начальной скоростью v0 = 5 м/с. Определить время полета тела и его скорость при соприкосновении с Землей. Силой сопротивления воздуха пренебречь. Построить графики зависимостей y(t), s(t), vy(t), ay(t).
| Дано: v0 = 5 м/с Н = 10 м |
|
Решение В любой точке траектории на тело действует только сила тяготения, т. е. движение происходит с постоянным ускорением
|
| t = ? v = ? |
В момент падения тела на Землю y = 0, тогда из уравнения 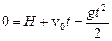 найдем время полета, т. е. t = 2 с.
найдем время полета, т. е. t = 2 с.
В момент падения тела скорость 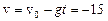 м/с (знак «–» показывает, что вектор скорости v направлен против выбранного направления оси Y).
м/с (знак «–» показывает, что вектор скорости v направлен против выбранного направления оси Y).
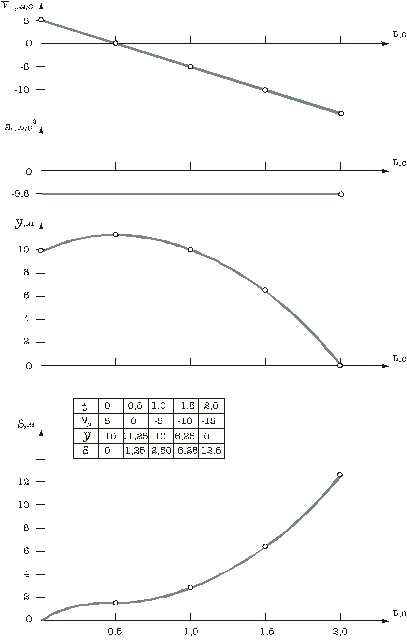 |
Задача 4. Из брандспойта (шланг с металлическим наконечником), расположенного около поверхности Земли, вырывается струя воды со скоростью v0 = 10 м/с. Брандспойт медленно вращается вокруг вертикальной оси, одновременно с этим меняется угол его наклона к Земле. Определить максимальную площадь, которую можно полить этим брандспойтом? Сопротивлением воздуха пренебречь. Считать g = 10 м/с2.
| Дано: v0 = 10 м/с |
Решение
|
| S = ? |
В выбранной системе координат
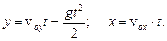
Максимальное удаление струи вдоль оси ОХ зависит от угла наклона брандспойта. Для (·) С y = 0, тогда 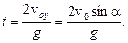 Дальность полета
Дальность полета 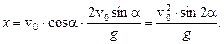 Очевидно, дальность полета максимальна, если 2a = 90°, т. е. a = 45°. Тогда максимальная дальность
Очевидно, дальность полета максимальна, если 2a = 90°, т. е. a = 45°. Тогда максимальная дальность 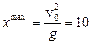 м. Максимальная площадь полива равна площади круга
м. Максимальная площадь полива равна площади круга 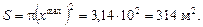
Задача 5. Тело бросили со скоростью 10 м/с под углом 45° к горизонту. Найти нормальное и тангенциальное ускорения и радиус кривизны траектории тела через 1 с после начала движения. Сопротивление воздуха не учитывать.
| Дано: vо = 10 м/с a= 45° t = 1 с |
Решение
|
| R = ? ап = ? a t = ? |
Направим оси ОХ и ОУ вдоль горизонтального и вертикального перемещений тела. Тело считаем материальной точкой. vох и vоу – проекции начальной скорости v0 на координатные оси. При движении тела vох не изменяется,
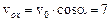 м/с,
м/с, 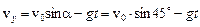 .
.
Через t = 1 с после начала движения
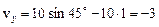 м/с,
м/с,
т. е. направлена вертикально вниз. Результирующая скорость в момент времени t = 1 с равна
 7,6 (м/с)
7,6 (м/с)
и направлена по касательной к траектории в точке В.
Обозначим угол между вектором 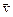 и осью ОХ через b. С течением времени угол b меняется. Разложив вектор
и осью ОХ через b. С течением времени угол b меняется. Разложив вектор 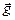 на составляющие по касательному и нормальному направлениям к траектории в точке В, получим:
на составляющие по касательному и нормальному направлениям к траектории в точке В, получим:
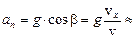 9,2 (м/с2),
9,2 (м/с2),
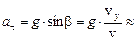 4,0 (м/с2).
4,0 (м/с2).
Радиус кривизны траектории в точке В вычислим по формуле
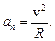
Подставив в последнее выражение значения v и an, рассчитанные выше, получим радиус кривизны: 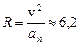 м.
м.
Задача 6. На барабан намотана нить, к концу которой привязан груз. Предоставленный самому себе, груз опускается с ускорением
5,0 м/с2. Определить ускорение точек, лежащих на ободе барабана, в тот момент, когда барабан сделает поворот на угол в 1 радиан.
| Дано: j = 1 рад wо = 0 а = 5,0 м/с2 |
Решение Полное ускорение точки обода
Для точек, вращающихся с постоянным ускорением, |
| а1 = ? |
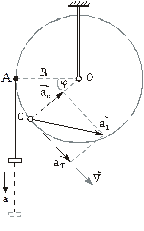
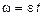 и
и 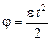 .
.
Линейная скорость v точек тела, удаленных от его оси вращения на расстояние R, равна v = wR. Тангенциальное (касательное) и нормальное ускорения этих точек связаны с кинематическими характеристиками вращательного движения тела формулами

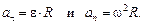
Зная угловое перемещение j, можно определить 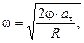 где
где 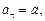 так как нить сматывается с барабана без проскальзывания.
так как нить сматывается с барабана без проскальзывания.
Определив 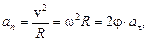 получим
получим

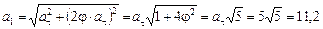 м/с2.
м/с2.
Задача 7. Якорь электромотора, вращающийся со скоростью
n = 50 об/с, двигаясь после выключения тока равнозамедленно, остановился, сделав N = 1500 оборотов. Найти угловое ускорение и продолжительность торможения.
| Дано: N = 1500 ν = 50 об/с ω = 0 |
Решение
Угловое ускорение якоря электромотора связано с начальной ω0 и конечной ω угловыми скоростями соотношением
|
| t = ? ε = ? |
откуда
 .
.
Но 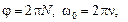 то
то  5,2 рад/с2.
5,2 рад/с2.
Знак минус указывает на то, что якорь вращался равнозамедленно. По условию задачи угловая скорость линейно зависит от времени
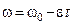 ,
,
отсюда
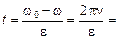 60,4 с.
60,4 с.
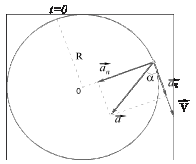
Задача 8. Материальная точка начинает двигаться по окружности радиуса R = 20 см с постоянным тангенциальным ускорением аτ = 0,5 см/с2. Через какой промежуток времени вектор ускорения 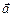 образует с вектором скорости
образует с вектором скорости 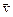 угол
угол 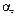 равный 30°? Какой путь пройдет за это время движущаяся точка?
равный 30°? Какой путь пройдет за это время движущаяся точка?
| Дано: v0 = 0 аτ = 0,5 см/с2 R = 20 см α = 30° |
Решение
Угол a между векторами
|
|
| t = ? S = ? |
 Тангенциальное ускорение
Тангенциальное ускорение
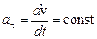 ,
,
следовательно, мгновенная скорость движущейся точки (при v0 = 0)
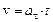 . (2)
. (2)
Подставляя (2) в формулу (1),
находим
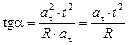 ,
,
тогда время 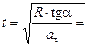 4,8 с,
4,8 с,
а путь  5,8 см.
5,8 см.
Последнее изменение этой страницы: 2019-03-22; Просмотров: 107; Нарушение авторского права страницы