
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Кинетическая энергия вращения ⇐ ПредыдущаяСтр 7 из 7
Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя частицами этого тела остается постоянным. В дальнейшем мы будем рассматривать только такого рода тела. Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси, проходящей через него. Мысленно разобъем это тело на элементарные массы m1, m2, …, mn, находящиеся на расстоянии r1, r2, …, rn от оси вращения. Угловая скорость этих материальных масс одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных масс:
Таким образом, кинетическая энергия вращающегося тела
Для тела (колеса), катящегося по горизонтальной поверхности, энергия движения будет складываться из энергии поступательного движения и вращательного:
где m – масса катящегося тела; v – скорость поступательного движения; J – момент инерции; w – угловая скорость вращения.
Моментом силы
Модуль момента силы
где a – угол между r · sina = l есть кратчайшее расстояние между линией действия силы и осью вращения и называется плечом силы. Направление момента силы (вращающего момента) определяется по правилу правого винта. Единица измерения момента силы
В случае действия нескольких сил результирующий момент сил равен векторной сумме моментов сил относительно оси:
При повороте тела на малый угол dj точка В пройдет путь
где a – угол между
но
поэтому
или
Учитывая, что
В векторной форме
или
Уравнение (1.12) представляет основной закон динамики вращательного движения: угловое ускорение тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту Моментом импульса материальной точки называется векторное произведение вектора
где
где Ji – момент инерции материальной точки; a = 90°.
т. е.
Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение (1.13) по времени:
т. е.
Уравнение (1.14) – еще одна форма закона динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси. Если мы имеем дело с замкнутой системой, то момент внешних сил
Выражение (1.15) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Из (1.15) следует, что если вращающаяся система может изменить момент инерции J под действием внутренних сил, то будет изменяться угловая скорость вращения w. Это правило используют танцоры, гимнасты при различного рода вращениях. Сопоставим основные величины и уравнения динамики поступательного и вращательного движения тела вокруг неподвижной оси, что может помочь при рассмотрении практических задач.
Примеры решения задач
Задача 1. Вычислить момент инерции тонкого однородного стержня массой m и длиной l относительно оси, перпендикулярной стержню и проходящей через его конец. Решение
Направим ось ОХ вдоль стержня AB. Mасса элементарного отрезка длиной dx
где Момент инерции элементарного отрезка длиной dx относительно оси
Момент инерции стержня
Задача 2. Вычислить момент инерции круглого однородного диска радиусом R и массой m относительно оси, перпендикулярной плоскости диска и проходящей через его центр.
Решение
где Момент инерции элементарного кольца относительно оси
Момент инерции диска относительно той же оси:
Задача 3. Вал в виде сплошного цилиндра массой m1 = 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2 = 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?
Решение
Линейное ускорение гири а равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности, и связано с угловым ускорением e вала соотношением
где r – радиус вала. |
| |||||||||||||
| а = ? |
Угловое ускорение вала согласно основному уравнению динамики вращающегося тела
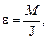 (1)
(1)
где М – вращающий момент, действующий на вал;
J – момент инерции вала относительно оси вращения, совпадающий с его осью симметрии.
Рассматриваем вал как однородный цилиндр. Тогда его момент инерции
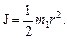
Вращающий момент, действующий на вал,
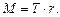
Найдем силу натяжения шнура Т по 2-му закону Ньютона:
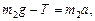
или
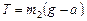
Таким образом,
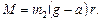 (2)
(2)
Подставив (2) в (1), получим:
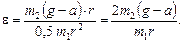
Зная e, выразим
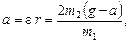
откуда
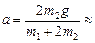 2,8 (м/с2).
2,8 (м/с2).
Задача 4. По наклонной плоскости, образующей угол a с горизонтом, скатывается без трения и скольжения сплошной однородный диск. Найти линейное ускорение центра диска. Решить задачу в общем виде, полагая, что вначале диск был неподвижен.
| Дано: a |
Решение |
| а = ? |
Пусть за t секунд центр тяжести диска прошел расстояние АВ = х от вершины наклонной плоскости, при этом потенциальная энергия диска уменьшилась на величину 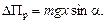
По закону сохранения энергии эта энергия перешла в кинетическую энергию диска в точке А:
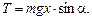 (1)
(1)
Кинетическая энергия диска складывается из кинетической энергии поступательного движения
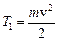 (2)
(2)
и кинетической энергии вращательного движения 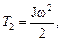 т. е.
т. е.
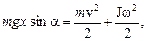
где J – момент инерции диска относительно оси, совпадающей с его геометрической осью;
 ; r – радиус диска; m – масса.
; r – радиус диска; m – масса.
Скорость поступательного движения диска v и угловая скорость вращательного движения диска w связаны соотношением
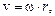
откуда
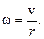 (3)
(3)
Подставив (3) в (2), получим
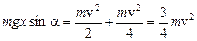 или
или 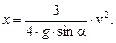
Дифференцируя это уравнение по времени t, получим:
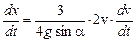 или
или 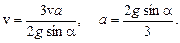
Задача 5. С какой скоростью должен въехать велосипедист в нижнюю точку мертвой петли радиусом R = 5 м, чтобы не сорваться вниз? Масса велосипедиста с велосипедом m = 100 кг, масса обоих колес m1 = 5 кг. Трением пренебречь, массу колес считать сосредоточенной в ободьях.
| Дано: m = 100 кг m1 = 5 кг R = 5 м |
Решение
|
| v0 = ? |
На основании закона сохранения энергии 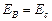 , т. е.
, т. е.
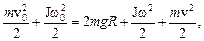 (1)
(1)
где 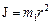 – момент инерции колес;
– момент инерции колес;
r – радиус колеса;
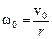 – угловая скорость колес в нижней точке петли ((·) В);
– угловая скорость колес в нижней точке петли ((·) В);
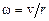 – угловая скорость колес в точке С.
– угловая скорость колес в точке С.
По второму закону Ньютона
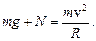
При N = 0 (условие обрыва)
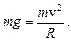 (2)
(2)
Решая систему уравнений (1) и (2), получаем
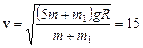 м/с.
м/с.
Задача 6. Тонкий однородный стержень длины l и массы m может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. Стержень приводят в горизонтальное положение и отпускают. Определить угловое ускорение и угловую скорость при прохождении стержнем положения равновесия.
| Дано: l, m |
Решение
|
| e = ? w = ? |
На стержень действует сила тяжести, приложенная в центре масс, и сила реакции оси. Вращающий момент создает только сила тяжести, так как линия действия силы реакции проходит через ось вращения. Согласно основному уравнению динамики вращательного движения
 (1)
(1)
где J – момент инерции стержня относительно оси О (по теореме Штейнера).
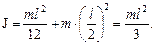
Если рассматривать движение стержня как движение в поле силы тяготения Земли, то по закону сохранения энергии
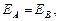
т. е.
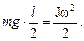 (2)
(2)
Решая полученную систему уравнений (1) и (2), находим
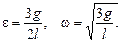
Задача 7. Горизонтальная платформа массой 80 кг и радиусом
R = 1,00 м вращается вокруг вертикальной оси, делая п1 = 30 об/мин. На краю платформы стоит человек и держит в расставленных руках гири. Какое число оборотов в минуту будет делать платформа, если человек, опустив руки, уменьшит свой момент инерции от 3,00 кг·м2 до 0,50 кг·м2? Считать платформу круглым однородным диском.
| Дано: R = 1,00 м т = 80 кг п1 = 30 об/мин J1 = 3,00 кг·м2 J2 = 0,50 кг·м2 | Решение По условию задачи платформа с человеком вращается с постоянной скоростью п1, поэтому результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы «платформа–человек» выполняется закон сохранения момента импульса:
|
| п2 = ? |
Подсчитаем начальный момент импульса системы L1 и конечное его значение L2:
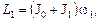 (2)
(2)
где 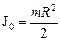 – момент инерции платформы;
– момент инерции платформы;
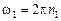 – ее начальная угловая скорость.
– ее начальная угловая скорость.
 (3)
(3)
где 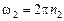 – конечная угловая скорость системы.
– конечная угловая скорость системы.
Решая систему (2)–(3), получаем:
 |
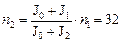 об/мин.
об/мин.
Последнее изменение этой страницы: 2019-03-22; Просмотров: 214; Нарушение авторского права страницы